RDPSO算法与K-Means聚类算法相结合的混合集群技术
2018-11-21张春燕
张春燕
(无锡科技职业学院,江苏 无锡 214028)
人类已经进入大数据时代,每天产生海量数据,机器学习[1]是一类用于自动化分析数据的工具的总称。
作为机器学习的算法之一——聚类分析是一种典型的无监督学习,用于对未知类别的样本进行划分,将它们按照一定的规则划分成若干个类簇,把相似(距离相近)的样本聚在同一个类簇中,把不相似的样本分为不同类簇,从而揭示样本之间内在的性质以及相互之间的联系规律。聚类算法在银行、保险、医学、军事等诸多领域有着广泛的应用[2]。K-Means算法[3]是基于划分的聚类算法,是公认的十大数据挖掘算法之一。
1 K-Means(K均值)聚类
算法步骤:
1) 首先我们选择一些类/组,并随机初始化它们各自的中心点。中心点是与每个数据点向量长度相同的位置。这需要我们提前预知类的数量(即中心点的数量)。
2) 计算每个数据点到中心点的距离,数据点距离哪个中心点最近就划分到哪一类中。
3) 计算每一类中心点作为新的中心点。
4) 重复以上步骤,直到每一类中心在每次迭代后变化不大为止。也可以多次随机初始化中心点,然后选择运行结果最好的一个。
这个过程直到两个计算结果不再变化,算法才收敛。从k-Means聚类的过程中,我们发现初始聚类中心对分类的影响很大,容易引起局部最优。以离群值为聚类中心的聚类效果最差,且聚类间分离没有得到有效的应用。我们通过建立一个新的模型来解决这些问题。为了优化新模型,引入了PSO算法。
2 PSO算法[4]
该算法将每个个体看作是在n维搜索空间中的一个没有重量和体积的微粒,该微粒以一定的速度飞行在搜索空间中。飞行速度由个体和群体的飞行经验进行动态调整。
设xi=(xi1,xi2,……,xid)为粒子i的当前位置;
vi=(vi1,vi2,……,vid)为粒子i的当前速度;
Pi=(Pi1,Pi2,……,Pid)代表粒子i的最佳适应性值,即pbest;
Pg=(Pg1,Pg2,……,Pgd)代表粒子群的最佳适应性值,即gbest。
粒子的速度更新见(1)和位置的更新见(2):
vij(t+1)=wvij(t)+c1r1j(t)[Pij(t)-xij(t)]+c2r2j(t)[Pgj(t)-xij(t)]
(1)
vij∈[-vmax,vmax]
xij(t+1)=xij(t)+vij(t+1)
(2)
c1,c2为加速常数,W为惯性权重。
PSO算法的缺点是容易出现早熟收敛,优化性能因此降低, 近年来,很多研究人员对PSO进行了研究并改进, 提出了算法的具体改进方案。Sun教授等以智能优化机制的基础——算法的个体学习能力和社会学习能力,结合了物理中金属导体自由电子具有的定向漂移运动方式和随机无规则的热运动方式,提出了一种改进的PSO算法——随机漂移粒子群(RDPSO)算法,该算法具有较强的全局搜索能力且不易出现早熟收敛。
3 RDPSO算法[5]
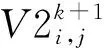
(3)
CJk为当前种群中所有粒子个体的历史最优位置平均值(mbest),m为种群规模,公式为
(4)
RDPSO算法中粒子速度和位置的更新公式为
(5)
(6)
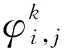
随机漂移粒子群的算法描述如下:
步骤1:给定了整体群体的大小, 粒子的位置和速度被初始化;
步骤2:通过公式(4)计算出所有粒子个体的历史最优位置平均值;
步骤3:根据目标函数值,更新了粒子的全局最优位置;
步骤4:根据目标函数值,更新了粒子的局部最优位置;
步骤5: 通过公式(5) 更新了粒子的速度;
步骤6:通过公式(6) 更新了粒子的位置;
步骤7: 如果满足结束条件, 则程序结束并输出结果,如果不满足,转入步骤 2继续执行。
4 RDPSO与K-Means算法相结合的混合集群技术[6-8]
给定了一个数据集 s,聚类的数目为 k,m为整个粒子群的种群数量。目标是得到聚类数据集的聚类中心不再变化的 k 个聚类划分。
步骤1: 数据集 s中随机选择 k 个中心点,作为粒子位置 Xi 的初值;
步骤2: Vi为粒子的初始化速度;
步骤3: 反复进行m次,共生成种群规模为m的初始粒子群;
步骤4: 根据目标函数值,更新粒子的全局最优位置;
步骤5: 根据目标函数值更新粒子的局部最优位置;
步骤6: 根据RDPSO算法中的(5)和(6)公式更新粒子的速度和位置;
步骤7: 对于选中的粒子,按照 K-Means聚类算法进行优化;
步骤8: 根据粒子的聚类中心编码作为初始值,该粒子的新的聚类划分根据最近邻法则来确定;
步骤9:结束条件为找到好的位置或者达到最大迭代次数,如果达到了结束条件则更新粒子并结束程序,如果不满足则转向步骤8继续执行。
5 实验
为了测试我们的实验有效性,我们选择了iris数据集150条记录、BreastCancer数据集569条记录、creditcard数据集284807条记录作为测试样本集,RDPSO-K-Means算法和PSO-K-Means算法进行了比较。PSO-K-Means聚类性能的结果如第一列所示,我们的算法聚类性能的结果如表1第二列所示。XB指标是寻找类内紧凑度和类间分离度之间的某个平衡点。常用于评价分类模型的好坏的一个常用评价标准就是Precision和Recall的加权调和平均F-Measure。在f-measure函数中,当参数α=1时,F1综合了P和R的结果,当F1较高时则能说明试验方法比较有效。
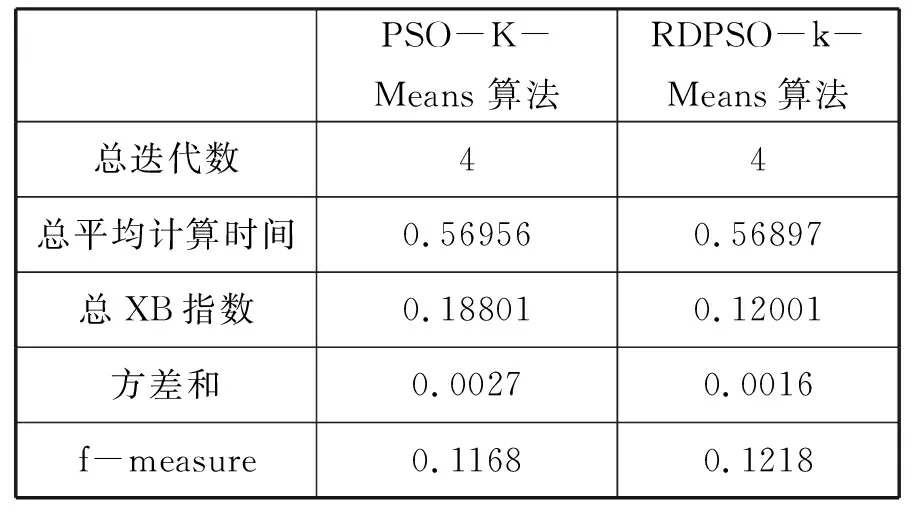
表1 PSO-K-Means算法和RDPSO-k-Means算法比较
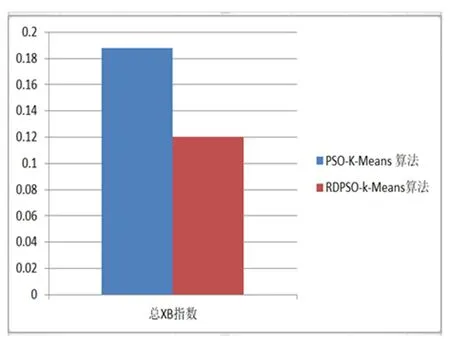
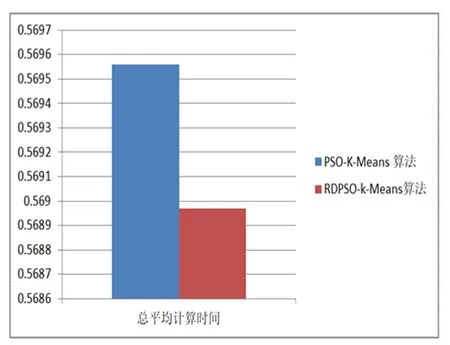
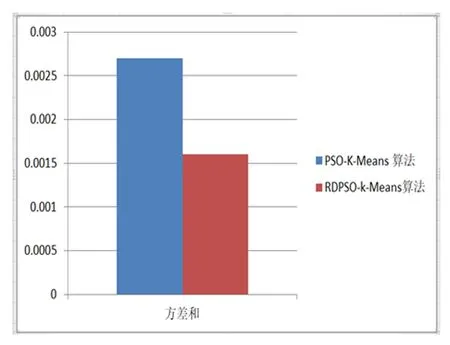
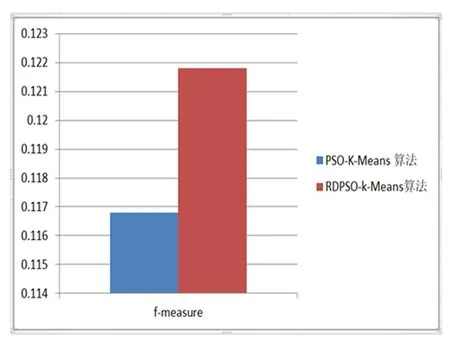
本文采用总平均计算时间、总XB指数、方差和f-measure四个参数进行结果分析。其中研究重点是尽量减少总平均计算时间、总XB指数和方差和,增加f-measure值。实验结果证明本文所应用的RDPSO算法与K-Means聚类算法相结合的混合集群技术性能明显优于PSO算法与K-Means聚类算法相结合的混合集群技术。
6 结论
K-Means算法经常由于初始值的选择问题而陷入局部最优解,而常见的PSO算法又容易陷入粒子群的早熟收敛,本文通过将聚类问题建立一种新的模型,并将RDPSO算法与K-Means算法相结合技术巧妙地引入到了目标函数中,充分考虑了集群的紧致性和群间的分离,从而使我们可以获得最终的聚类结果,从实验结果上取得了良好的效果。
