光学玻璃磁性复合流体抛光应力与材料去除率的实验研究
2018-11-21郝宇,姜晨
郝 宇, 姜 晨
(上海理工大学 机械工程学院, 上海 200093)
引 言
光学玻璃元件是各类光学仪器的核心组件如医疗内窥镜镜片、大型望远镜中光学零件、X射线波段工作仪器的反射面等[1]。光学玻璃元件制造过程中轴承振动、控制精度、加工工具磨损等因素,都会造成工件面形误差、亚表面损伤等缺陷[2]。强激光领域及其他光学技术领域的发展,对光学元件的制造提出更苛刻的要求,不仅要求具有很高的表面精度,还要求无亚表面损伤(subsurface damage,SSD)[3-4]。磁性复合流体抛光是基于磁流变抛光方法形成的新的抛光方法,能够在不产生亚表面损伤的情况下,快速有效地提高光学元件的表面质量[5]。
20世纪80年代中期,Tain和Kawata[6]研发了磁流体(magnetic fluid,MF)光整加工技术,他们借助磁场对聚丙烯工件进行抛光,工件表面粗糙度降低了10倍。1988年白俄罗斯学者Kordonski[7]提出磁流变抛光(magnetorheological finishing,MRF),并对一块直径50 mm的SLAM55非球面工件进行抛光,成功去除其5 μm的亚表面损伤层,面型精度P-V值由3.7 μm减小到0.2 μm。2002年,Shimada[8]将含有微米级磁性颗粒的磁流变液和纳米级磁性颗粒的磁性流体混合在一起,综合MF和MRF两者的优势,研制出磁性复合液体(magnetic compound fluid,MCF)。MCF抛光方式具有抛光效率高、不产生亚表面损伤、流变性能好和抗沉淀稳定性强等优势[9-11]。MCF抛光过程中工件的应力分布,是实现MCF确定性抛光的核心问题之一,直接决定了抛光过程的材料去除和表面质量。本文使用自行设计的抛光装置进行MCF抛光实验,分别检测自旋转MCF抛光和行星旋转MCF抛光的正应力和剪切应力分布并利用Taylor Hobson粗糙度仪检测抛光后材料的去除率,分析抛光效果,为MCF确定性抛光提供指导依据。
1 磁性复合流体抛光原理

表1 实验参数Tab.1 Experimental parameters
在外加磁场作用下,磁性复合流体形成具有剪切力的粘弹性Bingham流体,而磨料则均匀分布在磁性簇表面。抛光过程中,磁性簇与待加工工件表面发生挤压和摩擦作用,磁性簇中磨粒通过刮擦去除材料。实验中使用的抛光液是由铁粉(微米级的羟基铁粉、纳米级的四氧化三铁颗粒混合物)、水、氧化铈、α-纤维素按一定质量分数占比混合而成,各组分的质量分数占比分别为铁粉55%、水30%、氧化铈12%、α-纤维素3%。主要实验参数见表1。
2 抛光应力分布实验设计
抛光头结构示意图如图1(a),载液盘电机通过皮带带动右侧载液盘旋转。磁铁电机带动具有一定偏心距(e=8 mm)的磁铁旋转。实验中采用两种抛光方式进行抛光实验:自旋转抛光和行星旋转抛光。只有磁铁电机旋转的自旋转抛光方式,磁铁以一定偏心距绕主轴旋转,产生旋转磁场,带动抛光液旋转;磁铁电机和载液盘电机同时旋转的行星旋转抛光,抛光液既随着磁铁的旋转磁场运动,又随着载液盘旋转运动。
应力分布实验如图1所示,条形BK7工件(长55 mm×宽4 mm×厚6 mm)固定在Kistler测力仪垫板上。工件上表面设置一块厚3 mm的PMMA材质盖板,盖板中间开条型槽(长55.5 mm×宽4.5 mm)。工件上表面与盖板表面平齐,工件侧面与盖板不接触。移动工作台使工件中线经过MCF抛光头中心,且工件刚好接触到MCF抛光头如图1(b)所示。抛光应力实验实物图如图1(c)所示。实验设计工件进给步长L=2.5 mm,每个步长工件面积Ai=t×4=2.5×4=10 mm2。进给后抛光头驻留5 s,Kistler测力仪记录工件Y轴向切向力Fτ和Z轴向正应力Fn。实验过程,随着工件的进给,MCF抛光头施加给工件的力是不断叠加的,因此每个测量点的正应力Pi和剪切应力τi为:

图1 应力分布实验示意图Fig.1 Diagrammatic sketch of stress distribution experiment
实测MCF抛光头为一个直径约D=38 mm的规则圆形区域,设计n=D/2.5≈15个测量点进行应力分布实验。
3 实验结果及讨论
3.1 自旋转抛光实验
3.1.1自旋转抛光应力
自旋转抛光工件所受正压力如图2(a)所示,将工件受力测试结果代入式(1)、(2)得到抛光区域正应力分布如图2(b)。从图2(a)可以看出,MCF抛光头对工件的正压力随着MCF抛光头接触面积的增加而递增,最大正应力为1 N。工件受到的正应力呈W形分布,即抛光区域中心和外侧的正应力较大,其中最大正应力出现在中心区域,约为0.011 N,这是由于主轴带动磁铁产生的旋转磁场在抛光区域外侧磁场较强和磁场旋转挤压中间区域MCF抛光液所致。自旋转抛光正应力分布的对称中心在25 mm左右,可以看出有效抛光区域比实验实测的直径略大,直径约为50 mm。
自旋转抛光工件所受剪切力如图3(a) 所示,将工件受力测试结果代入式(1)、(2)得到抛光区域剪切应力分布如图3(b)所示。自旋转抛光工件所受剪切力呈先增大,最大值约为0.22 N,后减小的趋势。当进给总长度不超过MCF抛光头半径,工件的剪切力随着工件的进给增加;当进给总长度超过MCF抛光头半径,以MCF抛光头中心为分界点,工件受到方向相反的剪切力,部分剪切力被抵消,因此剪切力随着工件的进给而减少。从自旋转抛光工件剪切应力分布图可以看到MCF抛光头边缘对工件的剪切力比抛光头中心要大,最大剪切应力约为0.003 N。
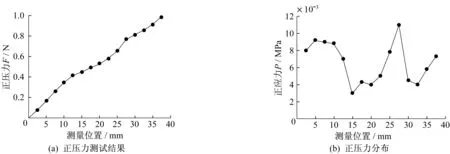
图2 自旋转抛光工件受到的正压力Fig.2 Positive pressure of workpiece by self-rotating polishing

图3 自旋转抛光工件受到的剪切力Fig.3 Shearing force of workpiece by self-rotating polishing
3.1.2自旋转抛光材料去除率
自旋转抛光BK7玻璃工件工作50 min。利用Taylor Hobson粗糙度测量仪检测加工完成后抛光痕迹的深度,计算得到工件的材料去除率如图4所示。工件表面材料去除率分布曲线呈W型。加工区域外侧材料去除率较大,最大约为0.011 μm/min,这是由于加工区域外侧剪切应力较大所致。

图4 自旋转抛光工件材料去除率Fig.4 Material removal rate of workpiece by self-rotating polishing
3.2 行星旋转抛光实验
3.2.1行星旋转抛光应力
行星旋转抛光工件所受正压力如图5(a)所示,将工件受力测试结果代入式(1)、(2)得到抛光区域正应力分布如图5(b)。正压力随着MF抛光头作用在工件上的面积的增加而递增,最大为0.8 N。正应力在抛光头直径方向上的分布呈‘凹’字形,工件接触抛光液外侧的区域收到的正应力较大,其中最大正应力为0.007 3 N。
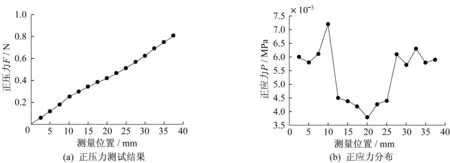
图5 行星抛光的正应力Fig.5 Positive stress of workpiece by planet-polishing
行星旋转抛光工件所受剪切力如图6(a) 所示,将工件受力测试结果代入式(1)、(2)得到抛光区域剪切应力分布如图6(b)。剪切力呈中心对称,随着作用面积的增加先递增后递减,其中最大剪切力为0.23 N。行星旋转抛光工件剪切力与行星旋转抛光工件所受正压力分布相似,都是呈‘凹’字形,外侧最大剪切力为0.004 2 N。

图6 行星旋转抛光工件受到的剪切力Fig.6 Shearing force of workpiece by planet-polishing
3.2.2行星旋转抛光材料去除率
行星旋转抛光BK7玻璃工件工作50 min,工件的材料去除率如图7所示。材料去除率分布曲线呈现中间高两侧低的山丘形状,除去率从抛光区域中心到边缘递减,最大的材料去除率出现在工件中心区域附近,约为0.038 μm/min。行星旋转抛光材料去除率明显大于自旋转抛光材料去除率,这与行星旋转抛光工件受到剪切应力大的实验结果吻合。
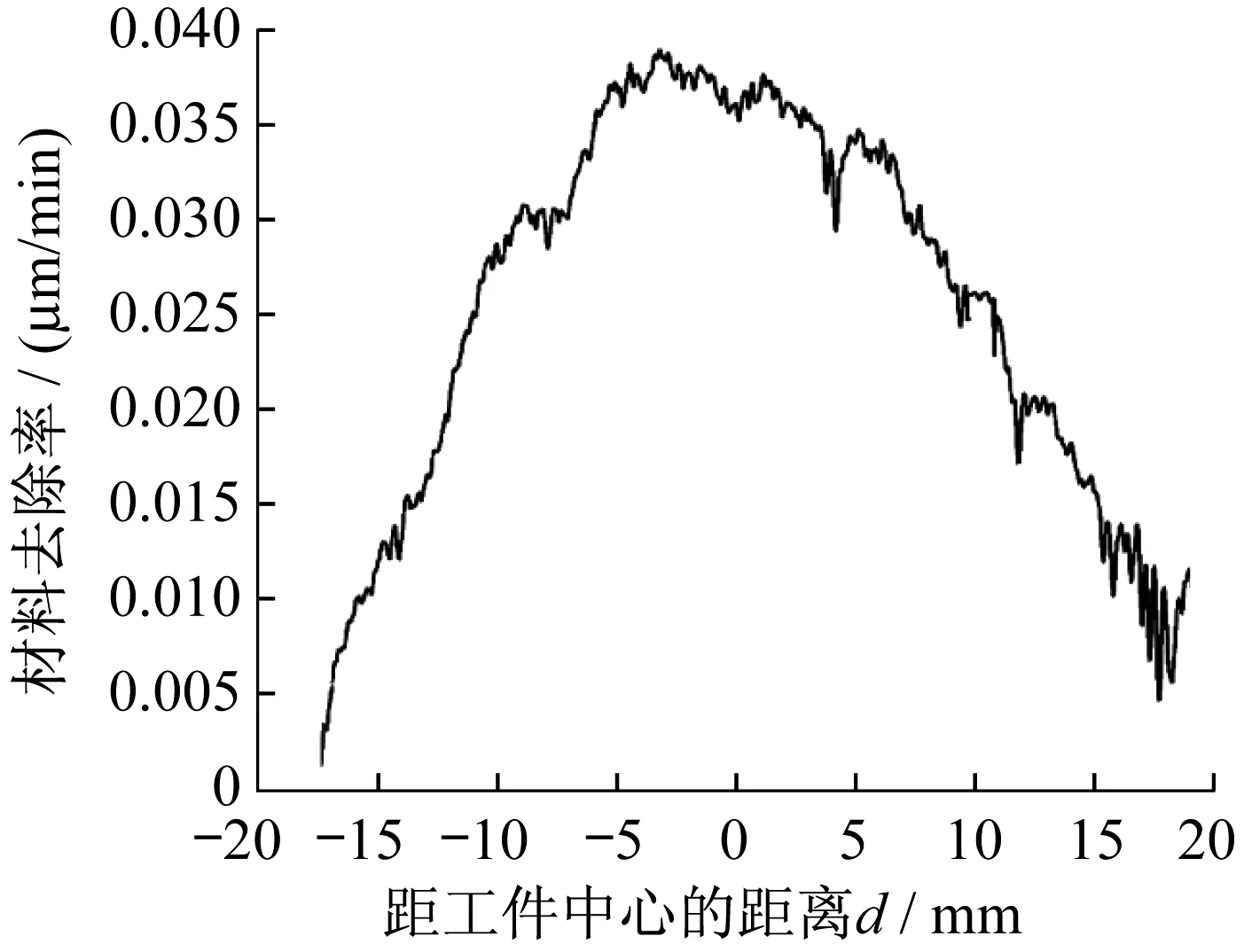
图7 行星旋转抛光工件材料去除率Fig.7 Material removal rate of workpiece by planet-polishing
4 结 论
1) 通过自旋转式和行星旋转式抛光应力实验,发现两种抛光中正应力均明显大于剪切应力,工件外侧剪切应力大于中心剪切应力。
2) 进行抛光加工,检测工件表面形貌,结果表明行星旋转抛光式材料去除率明显大于自旋转抛光。
