基于拉盖尔-高斯光束的螺旋干涉模式研究

谢继龙, 王 宁, 陈明明, 贾宏志

(上海理工大学 上海市现代光学系统重点实验室, 上海 200093)

引 言

光镊技术[1]经过长期的发展,其粒子捕获能力得到了极大的提升。光镊中的光子与介质微粒进行动量交换时,在梯度力和散射力的共同作用下,微粒被稳定束缚在激光焦点附近,其中使粒子沿着光束传播方向运动的力,称为散射力;使粒子向光束焦点运动的力,称为梯度力,指向光场强度的最大处且正比于光强梯度。多数研究通过改造光源光强的分布来提高光镊的捕获能力[2]。Ashkin[3]研究了TEM01(具有环状光强分布)光束的粒子捕获能力。Gussgard等[4]利用光阑,在高斯光束中心产生一个暗场来实现环状光强分布,从而提高了高斯光束的轴向粒子捕获能力。然而,这种方法的操控难度较高,不利于粒子的精确控制。拉盖尔-高斯光束是光子轨道角动量的本征态,具有光子角动量,比高斯光束[5]有着更强的粒子捕获能力[6]。通常可以采用衍射光栅[7]、螺旋相位片[8]和全息叉形光栅[9]等方法获取拉盖尔-高斯光束。若将两束拉盖尔-高斯光束的同轴叠加,可干涉产生具有螺旋光强的光束,这种光束即光镊可以提高光束对粒子的操控的灵活度。尽管使用旋转光阑、旋转镜和莫尔技术等方法可以产生螺旋光强光束,但基于拉盖尔-高斯光束干涉而形成螺旋光强光束的方法更加简单、方便和灵活。本文首先对拉盖尔-高斯光束的同轴叠加进行了一定的理论分析,给出了不同参数对场强分布的影响。通过仿真模拟,计算出不同参数的具体场强分布,更加直观地展现出了不同参数对场强的影响。

1 理论分析

在柱坐标系下求解傍轴亥姆霍兹方程,得到一组完全解,整理得到的拉盖尔多项式与高斯函数的乘积的形式称为拉盖尔-高斯光束[10],表示为

(1)

式中:C为归一化因子;u(r,θ,z)为柱坐标系中拉盖尔-高斯光束的空间分布函数;r为原点O到某点在平面xOy上的投影的距离,r∈[0,+∞);θ为从正z轴来看自x轴按逆时针方向转到某点转过的角,θ∈[0,2π);z为圆柱高度,z∈R;k=2π/λ是真空中的波数;m为拓扑电荷数(取整数),表示拉盖尔-高斯光束中每个光子所携带的轨道角动量数;z0是瑞利长度;R(z)是波前曲率半径随传输距离的变化函数;w(z)是光束宽度随传输距离的变化函数。其中z0、R(z)、w(z)分别表示为:

式中w0=(λz0/π)1/2为束腰半径。当式(1)中的m取0时,拉盖尔-高斯光束会退化为基模高斯光束[11-12]。令

(5)

此时式(1)可以改成

(6)

用下标01和02分别表示拉盖尔-光束1和2,其共轴叠加的场强方程可表示为

(7)

其中P1和P2分别为

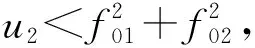
2 仿真模拟

在波长确定的情况下,P1与P2的值主要由m1、m2和束腰半径的值来确定。用MATLAB软件对两束拉盖尔-高斯光束同轴叠加进行了仿真,并对其叠加后的场强进行分析,对比了不同参数变化所带来的场强变化。在束腰半径相同的情况下,改变m1和m2的值得到如图1所示的结果。图1中(a)(b)(c)分别为|m1-m2|的值等于4、3和2时的场强。可以看出,图1中(a)、(b)、(c)的场强结构周期分别为1/4、1/3和1/2,这刚好说明仿真结果和理论分析结果基本一致,即场强是一个周期为1/(|m1-m2|)的结构分布图。

图1 在束腰半径相同的情况下不同m1、m2的场强Fig.1 The intensity distribution for the same beam waist and different m1 and m2

在束腰半径不同的情况下,再次改变m1和m2的值,其仿真结果如图2所示。图2中(a)(b)(c)分别是m1-m2的差的绝对值等于2、3和4的场强分布图。观察到图2(a)(b)(c)中的场强结构周期分别为1/2、1/3和1/4。对比图1,虽然与图2有明显的差别,但场强依然是一个周期为1/(|m1-m2|)的结构。

图2 在束腰半径不同且m1

图1和图2所示结果都在m1m2,仿真得到如图3的场强分布结果。图3中场强分布结构依然是周期为1/(|m1-m2|)的结构图。将图3中的(a)、(b)、(c)分别与图2中的(a)、(b)、(c)相加会发现其电场分布刚好互补,即叠加后的场强周期结构会消失。

图3 在束腰半径不同且m1>m2的情况下不同m1、m2的场强Fig.3 The intensity distribution for the different beam waists and m1>m2

3 结 论

本文对两束拉盖尔-高斯光束的同轴叠加进行了理论推导和分析,通过MATLAB仿真对比了不同m1、m2和w0对场强结构的具体影响。结果表明,两束拉盖尔-高斯光束的同轴叠加干涉所产生的螺旋模式其场强的螺旋“叶片”数量和|m1-m2|有直接的关系,并且束腰半径的改变也会引起场强整体的变化,仿真得到的结果与理论模型基本吻合。利用该干涉模式操控微粒子,调节拉盖尔-高斯光束的拓扑电荷数,可以更加灵活的操控微粒。这种干涉模式的研究为提高微粒子的操控精度提供了一个有效可行的方法。