等维灰色模型在徐州地铁监测中的应用

2018-11-20董长江孙成勇

智能城市 2018年20期

李真张澄董长江孙成勇

中国建筑西南勘察设计研究院有限公司，上海 200120

随着地铁工程在各大城市如火如荼的展开，加之地铁工程基坑挖深大，地铁线路往往穿梭于各大城市中心区域，地铁车站及区间周边环境较为复杂，故而对监测技术提出了很高的要求。随着测绘技术的发展和测绘仪器的进步，所得到的测量数据增加迅速，而且各观测数据存在着非线性、随机性、相关性等特点，加上测量数据存在着粗差与噪声，所以需要更为科学的数据处理理论，有效率的利用数据资料，通过分析和计算，得到准确的风险评估和风险预报。

1 灰色预测模型与GM（1,1）

灰色理论（简单称GS理论）提出于20世纪80年代，提出者为我国华东理工教授邓聚龙。灰色系统所研究的对象是凭信息的建模。灰色模型是把所有的随机过程看成为一定范围内变化的并且与时间相关的灰色过程。它将杂乱无章的原始数据通过一定的数理方法整理成规律性较强的数列后再做研究，是灰色量用数据生成的方法，而不是从寻求统计规律的角度，通过大量样本进行研究。灰色系统自提出以来，经过一代人不断的努力有了飞速的发展，监测工作者现广泛把灰色理论应用于地铁的变形监测数据处理与分析中。

1.1 灰色预测模型GM（1,1）的建立

GM（1,1）灰色预测模型的建立的步骤为：

（1）设原始数据序列为

由此可以得到一个新的数列：

这个通过原始数列累加得到的新数列相较于原始数列，弱化了原始数列所具有的随机性，增加了原始数列所欠缺的稳定性。

（2）对于新数列所具有的特征，选用一阶微分方程来描述其变化的特征：

通过最小二乘法，拟合得到参数a和b的值：

由上可以假设灰色微分方程为：

式（6）微分方程即为GM（1,1）灰色预测模型。

（3）数据矩阵的构造：

（4）通过微分方程求解的结果：

则灰色模型GM（1,1）的响应时间序列为：

1.2 灰色预测模型残差检验

残差检验是指灰色预测模型的预测值与实际观测值之差，即模型计算值：

1.3 灰色预测模型的后验差检验

用灰色模型得出的预测值是否具有可信度，要通过一些必要的数理检验才可得知。在残差预测模式中，检验的数据不能通过一次计算得出，而要通过后面的数据推算前面的数据，这样依次检验，每一个检验值对灰色预测模型来说都是后验值，所以这种验证方法称为后验差检验。

后验差检验用到的数据是：

还需要求得残差的离差：

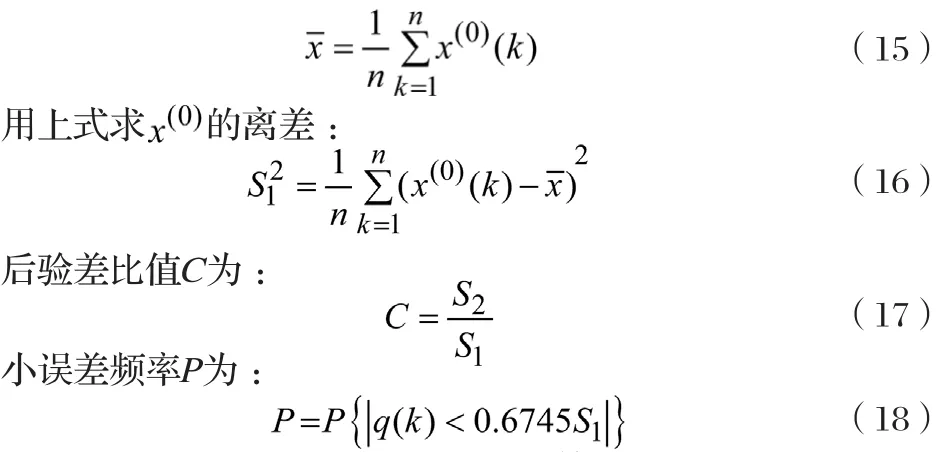
P和C是后验差检验的两个最为重要数据。

一般将模型的精度按P、C值划分为四个等级，如表1所示。

表1 模型预测精度分级

灰色预测模型的精度等级=max{P所在的等级，C所在的等级}，如表2所示。

表2 模型预测精度分级

2 地铁工程实例分析

2.1 预测模型的建立

本文对徐州地铁某车站地表沉降监测点的大量数据进行了处理和拟合，得到了相似的结论。同样选择地表沉降深层监测点SC21数据为例。选取前24期数据为训练数据，以此预测第25期的数据。

利用所编写的MATLAB程序来进行建模预测。将原始观测数据作为训练数据带入到MATLAB程序中去，经过解算求得参数a=-0.0028，b=-5.1684。

2.2 预测模型精度的评定

2.3 累计沉降值的预测

利用该等维的灰色预测模型预测该地表沉降监测点SC21的累积沉降位移变化量进行预测，得到预测值与实测值对比曲线图如图1所示。

按照残差计算公式，对上述预测模型进行精度评定，得到残差编号曲线图如图2所示。

图2 残差变化曲线图

由上述曲线图显示，灰色预测模型在预测精度上良好，符合预测的要求，故而可以应用于实际的地铁工程建设监测预报中去。由于本文所采用的是等维的灰色预测模型，即在预测的时候，所选用的训练数据个数的固定的，但是每次预测时，都会淘汰掉最前面的一个观测数据，而补充进去最新的观测数据作为训练数据，极大程度地削弱了时间序列数据在预测长期数据时精度下降的问题，所以等维的灰色预测模型可以用来预测长期地表沉降累计变化值。