高速公路主线相互合流至出口最小间距的研究

杨少伟，赖泓志，潘兵宏，姚 晶，严考权

1)长安大学公路学院，陕西西安 710064；2)长安大学特殊地区公路工程教育部重点试验室，陕西西安 710064

主线相互合流是交通流转换的重要形式．若高速公路中主线相互合流接主线出口段的间距过小，将使驾驶员不能完全掌握交通信息和实际路况，导致车辆不能及时换道，进而造成车辆在主线出口处紧急刹车和换道，对主线的交通流造成严重影响，甚至发生车祸．根据中国陕西省某高速公路某服务区的主线出口事故统计，在2007—2009年，高速公路主线出口的事故次数分别为36次、98次和42次，占该段服务区区域事故率的37.89%、38.58%和40.38%，为高事故率区域．因此，对深入研究高速公路主线相互合流至主线出口最小间距具有重大意义．

目前，中国规范尚无对高速公路主线相互合流至主线出口最小间距的建议值，国际上也少有该方面的研究论文，由于较早的设计采用主线相互合流的形式较少，因此对其研究仍处于空白．但是基于研究原则和研究类型的相似性，相关领域的研究对于分析主线相互合流至主线出口最小间距有一定的借鉴．《日本公路技术标准的解说与运用》[1]与《日本高速公路设计要领》[2]考虑出口预告标志设置安全距离的要求，规定高速公路互通式立交最小间距为3 km；中国《公路立体交叉设计细则》[3](以下简称《细则》)规定，一般互通式立交之间的最小间距为4 km，一般互通式立交与枢纽互通式立交之间的最小间距为4.5 km；杨少伟等[4]基于交通冲突技术研究了互通立交主线入口至前方出口的最小净距；黄治炉等[5]通过建立变道模型计算得到互通立交主线入口至前方出口的最小净距．由于互通式立交主线入口为匝道接入，合流时速度较低，且合流后的交通流特性与主线相互合流后的交通流特性不同，故此类研究与本研究存在很大的差异性．本文通过研究主线相互合流的交通流特性、驾驶人识读标志、换道行为和轨迹、确认出口及出口减速段等相关方面，建立基于不同车道数、不同合流方式的最小间距计算模型，提出高速公路主线相互合流至出口最小间距建议值，并对建议值进行仿真验证．

1 最小间距定义

主线相互合流至前方主线出口的间距是指在满足通行能力、保证交通安全和服务水平的前提下，合流鼻至主线出口小鼻点之间的距离．考虑最不利情况，即驾驶员不熟悉路况，不知道主线相互合流后紧接主线出口，则最小间距具体包括主线相互合流构造距离L1、 车流重分布距离L2、 认读标志距离L3、 车辆换道距离L4、 安全确认距离L5及出口减速段距离L6， 如图1．

图1 间距组成示意图Fig.1 Schematic of spacing composition

当进行1次换道时，所需要的1次换道距离LH可分为等待可插入间隙距离LH1、 驾驶员判断距离LH2、 驾驶员调整距离LH3和实施换道距离LH4， 如图2．则L2和L4为L2(4)=nLH， 其中，n为车流重新分布距离和车辆换道距离中进行换道的次数．

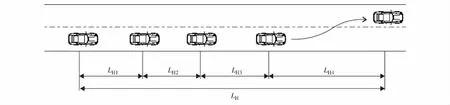
图2 车辆进行1次换道的距离Fig.2 The distance of a vehicle to change lane at one time

2 影响因素分析

2.1 主线相互合流方式

左右侧直接合流和左行线从右侧合流是主线相互合流的主要方式， 根据交通量的不同， 具体分为

1)在主线相互合流前的交通量中，当来自左侧的交通量与主交通流或左右侧交通量大小相当时，宜采用从左侧直接合流，即左右侧直接合流的方式．

2)在主线相互合流前的交通量中，当来自左侧的交通量为次交通量时，宜采用左行线从右侧合流的方式．

3)当主线相互合流前的交通量均接近设计通行能力时，可按原有车道数直接合流．

4)当合流前其中一侧的交通量接近设计通行能力、另一侧交通量较小时，交通量较小的一方应从右侧合流，且合流后可减少1个车道，但应设置不小于400 m的辅助车道进行过渡．

5)当合流前来自两侧的交通量均较小时，合流后可减少1个车道，并可采用直接合流的方式．

2.2 换道分析

2.2.1 主线相互合流后车流重新分布

中国的高速公路将行车道分为客车车道和货车车道，采取客货分离的组织方法，因此，主线相互合流后的车流需重新分布．对需要进行强制换道的最不利情况进行分析，主要为左侧交通量的大型车(本研究将半挂列车作为大型车的代表车型)向右变道至大型车车道或右侧交通量的小型车(本研究将小客车作为小型车的代表车型)向左变道至小型车车道的情况，且左右侧直接合流和左行线从右侧合流的最不利情况相同，因此本文选取左右侧直接合流的方式进行研究，分析结果如下：

1)单向三车道高速公路

单向三车道高速公路主线相互合流有2种情况：① 2条单向两车道高速公路通过合流渐变段直接合流为1条单向三车道高速公路，定义为2+2-1=3类型，其最不利情况为左方交通流中外侧大型车需要进行1次换道至最外侧车道，如图3(a)；② 2条双车道高速公路利用辅助车道合流为1条单向三车道高速公路，定义为2+2=4=3+1类型，其最不利情况为左方交通流中外侧大型车需要进行1次换道至外侧车道，右方交通流中内侧小型车需要进行1次换道至内侧车道，如图3(b)．

2)单向四车道高速公路

单向四车道高速公路主线相互合流有3种情况：① 2条单向双车道高速公路直接合流为1条单向四车道高速公路，定义为2+2=4类型，其最不利情况为左方交通流中外侧大型车需要进行2次换道至最外侧车道，如图4(a)；② 1条单向三车道高速公路与1条单向双车道高速公路通过主线相互合流渐变段合流为1条单向四车道高速公路，定义为3+2-1=4类型，其最不利情况为左方交通流中外侧大型车需要进行1次换道至最外侧车道，如图4(b)；③ 1条三车道高速公路与1条单向双车道高速公路利用辅助车道合流为1条单向四车道高速公路，定义为3+2=5=4+1类型，其最不利情况为左方交通流中外侧大型车需要进行1次换道至外侧车道，右方交通流中内侧小型车需要进行1次换道至内侧车道，如图4(c)．

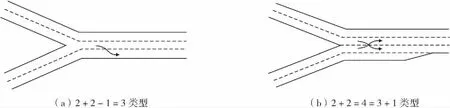
图3 单向三车道合流示意图Fig.3 Unidirectional three-lane confluence

图4 单向四车道合流示意图Fig.4 Unidirectional four-lane confluence

2.2.2 换道类型

由于车辆的车型因素，最外侧的大型车车道和内侧的小型车车道出现可插入间隙时间不相同．中国的高速公路将行车道分为客车车道和货车车道，在主线相互合流过程和主线出口前换道过程中，考虑不同车型的车辆均有可能向内或向外换道，因此将具体换道划分为：小型车进入小型车道、小型车进入大型车道、大型车进入大型车道以及大型车进入小型车道4种类型．

2.3 各个部分影响因素确定

L1的主要影响因素为合流前左右两侧主线的平曲线半径及合流渐变率；对于L2和L4， 由于驾驶员需要操作车辆进行换道，其主要影响因素为车辆换道类型、换道次数、交通量及驾驶员行为特征；对于L3和L5， 由于驾驶员需进行标志认读和确认分流点，其主要影响因素为驾驶员行为特征及心理反应．

3 计算模型建立

3.1 主线相互合流构造距离L1

L1是指设置主线相互合流交通设施所需要的长度．由上述分析可知，有多种主线相互合流方式，包括合流鼻与合流点间的距离、主线相互合流渐变段长度、辅助车道长度及渐变段长度．

3.1.1 合流鼻与合流点之间的距离

由于主线相互合流时速度较高，为保证行车安全和舒适，在合流点之前令其路拱横坡保持一致，据此提出假设，建立合流鼻与合流点之间的距离计算模型，假设① 合流鼻与合流点之间两条高速公路线形为半径相同、偏向相反的两圆曲线；② 合流点处的偏角与主线相互合流设计终点有相同的渐变率；③ 由于采用圆曲线半径较大，忽略行车道宽度及硬路肩宽度的影响；④ 认为合流鼻与合流点之间的距离，为合流鼻至合流点之间的直线距离，而不是任意一条高速公路的行驶路径．

根据上述假定，建立合流构造距离模型如图5．其中，点M和N分别为合流鼻和合流点；MN为合流构造距离；点OA和OB为2条高速公路合流处圆曲线的圆心；OAM和OBM为各自高速公路小鼻点处偏置加宽后硬路肩外边缘线半径且相等；OAN和OBN为各自高速公路最外侧行车道外边缘线半径且相等．

图5 合流构造距离模型Fig.5 Distance model of confluence structure

由图5几何关系可知

(1)

(2)

(3)

其中，MN为分流构造距离(单位：m)；OAM为硬路肩边缘线半径(单位：m)；OAN为行车道外边缘线半径(单位：m)；α为合流点处两条行车道的偏角(单位： °)．

根据上述假定，由于2条高速公路为反向曲线，为保证行车安全，在合流鼻之前令其路拱横坡保持一致，考虑到半径较小时，其中一条高速公路会出现反超高情况，因此，取合流鼻与合流点之间的最小半径为不设超高最小半径．α可按照车辆分流起点的最大渐变率取值，根据《细则》中规定渐变率不应大于1/80，计算得α=0.716°，可得当设计速度分别为120 km/h、100 km/h和80 km/h时，合流构造距离分别为34 m、25 m和16 m．

3.1.2 主线相互合流渐变段长度

主线相互合流渐变段是指合流点至合流终点的距离．当主线相互合流的方式是直接减少1条车道的合流方式，即存在合流渐变段时(如2+2-1=3类型)，根据《细则》规定的渐变段值为不小于300 m，本研究取300 m；若为其他合流方式时，合流渐变段长度为0．

3.1.3 辅助车道长度及渐变段长度

当主线相互合流的方式为需要通过辅助车道过渡渐变减少1个车道时，如2+2=4=3+1类型，车流重新分布可在辅助车道进行，但辅助车道长度需与车流重分布所需长度相比较后取较大值．《细则》中规定辅助车道长度不小于400 m，本研究取400 m；结合美国《道路设计与环境手册》和《日本高速公路设计要领》综合考虑，取渐变段的渐变率为1/50，因此，渐变段长度为200 m．

3.2 车辆重新分布距离L2

根据《公路路线设计规范》[6]高速公路设计服务水平应不低于3级，互通式立交匝道、分合流区段以及交织区段，设计服务水平可降低1级，因主线相互合流后设计速度不变，为表示交通流状态处于稳定流的中间范围并结合中国国情，故本研究基于3级服务水平对最小净距进行研究．

主线相互合流后车辆需要换道行驶在规定的车道上，车辆重新分布距离由等待可插入间隙距离LH1、 驾驶员判断距离LH2、 驾驶员调整距离LH3及车辆换道距离LH4组成，每部分计算过程如下．

1)等待可插入间隙距离

由可插入间隙理论知，当在3级服务水平下车辆处于稳定流状态时，车头视距服从M3分布[7]，车辆等待可插入间隙时间tw为

(4)

其中，tc为换道车辆所需临界间隙，取值为3.5～4.0 s[8]，本研究小型车取3.50 s，大型车取3.75 s；τ为车辆之间保持的最小车头时距，取值1.0～1.5 s[9]，本研究小型车车道取1.2 s，大型车车道取1.4 s；α为按自由流状态行驶车辆所占的比例[10]，本研究在设计速度为120 km/h、100 km/h及80 km/h时，小型车车道分别取值0.628、0.647及0.685，大型车车道分别取值0.525、0.547及0.591；λ为特征参数，本研究基于3级服务水平，在120 km/h、100 km/h及80 km/h时速下，小型车车道分别取λ=0.640、0.617及0.571，大型车车道分别取λ=0.671、0.643及0.590．

不同换道类型所需平均等待可插入间隙时间见表1．

表1 等待可插入间隙时间Table 1 Waiting insertion interval time

1)“小→小”表示小型车进入小型车道类型

等待可插入间隙距离LH1为

(5)

其中，vH1为车辆等待可插入间隙时的运行速度(单位：km/h)，此时车速约为基本路段运行速度的0.76倍[11]；tH1为等待可插入间隙所需时间(单位：s)．

2)驾驶员判断距离

在出现可插入间隙时，驾驶员需要判断此间隙是否为可插入间隙，驾驶员判断距离为

(6)

其中，LH2为判断是否为可插入间隙的距离(单位：m)；vH2为判断时的运行速度(单位：km/h)，与等待可插入间隙的运行速度相同；tH2为判断是否为可插入间隙所需时间(单位：s)，根据相关研究表明，驾驶员反应时间为0.5～4.0 s，本研究取2.5 s．

3)驾驶员调整距离

驾驶员确定出现的间隙为可插入间隙后，自身车速与目标车道车速有速度差，进行换道时，车辆需与可插入间隙并行，因此车辆需要调整车位及车速，令自身车速与目标车道车速一致．驾驶员调整距离计算公式为

(7)

其中，LH3为驾驶员调整所需距离(单位：m)；v0为调整车位前的运行速度(单位：km/h)；vt为调整完成后的运行速度(单位：km/h)；tH3为驾驶员调整所需时间(单位：s)，相关研究表明[12]，tH3=2.5 s．

4)实施换道距离

驾驶员完成上述3个过程后实施换道，实施换道过程是先加速后减速、最后匀速行驶的过程，其换道轨迹符合五阶多项式换道轨迹，且纵向约束条件为5个，横向约束条件为6个(其中，可通过假设将横向未知参数全部求出)，故本研究采用五阶多项式确定车辆的换道轨迹，以确定车辆换道过程中所需距离，如图6．其中，X(t)表示车辆纵向位移，Y(t)表示车辆横向位移，具体为

X(t)=A5t5+A4t4+A3t3+A2t2+A1t+A0

Y(t)=B5t5+B4t4+B3t3+B2t2+B1t+B0

(8)

其中，Ai和Bi为函数式所需的未知参数；t为换道过程中消耗的时间(单位：s)．

图6 五阶车辆换道模型Fig.6 Five-stage vehicle lane changing model

图6为五阶车辆换道模型．可见，开始换道时车辆位于所在车道的中心线上，运行速度为目标车道车辆的速度或车辆所能达到的最大速度，之后开始加速转向进行换道，侧向驶入目标车道，车辆到达目标车道时驾驶员开始减速并调整车位，令车速和位置与目标车道相匹配．根据分析换道具体过程，得到横向和纵向的约束条件，见表2．其中，T为整个换道操作过程所需时间(单位：s)；W为车辆横移距离(单位：m)，本研究取3.75 m；V为车辆准备换道和换道结束时刻的运行速度(单位：m/s)．

表2 约束条件Table 2 Constraint condition

由表2约束条件可知，横向为6个约束条件，可将未知参数全部求出；纵向为5个约束条件，缺少1个条件，令A5=m并参与计算．对式(8)进行求导，将所有约束条件代入计算，并进一步求导得

(9)

(10)

相关研究表明[13]，当横向最大加速度amax≤1.8 m/s2时，乘客感觉舒适，故令Y‴(t)=0， 求出Y″(t)的最大值为

(11)

即

(12)

查阅文献[14]，取小型车换道操作持续时间为3.5 s，大型车换道操作持续时间为4.0 s．

对于纵向而言，车辆行驶仍需满足行驶舒适性，即车辆在行驶过程中的最大加速度为1.8 m/s2，且需要满足最大刹车加速度aBmax， 如式(13)．

X″(t)∈[aBmax,amax]

(13)

对X″(t)取极值，即令X‴(t)=0， 则

(14)

当m>0时，

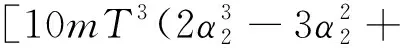
当m<0时，

综上公式得

m∈

将所需参数代入计算得

mt∈[-0.029, 0.029]

mc∈[-0.045, 0.045]

(15)

考虑最不利情况，取m为最大值，故车道换道距离为

(16)

其中，Sc和St为小型车与大型车换道操作过程所需长度(单位：m)；Vc和Vt为小型车与大型车准备换道和换道结束时刻的运行速度(单位：m/s)；Tc和Tt为小型车与大型车换道操作过程所需时间(单位：s)．

5)车辆重新分布距离L2

由于主线相互合流方式的不同，车辆重新分布时所需变换车道的次数和换道类型也不同，具体情况所需要的车辆重新分布距离见表3．

表3 不同合流方式所需车辆重新分布距离Table 3 The redistribution distance of vehicles required by different confluence modes

3.3 认读标志距离L3

在车辆重新分布完成后，驾驶员应能马上看见提示前方主线出口的交通标志．驾驶员认读标志距离包括识读标志距离和决策距离，具体计算过程如下．

3.1.1 识读标志距离Lr

有关研究表明[15]，驾驶员识读标志的时间为2.6 s，此时车辆匀速行驶，则

(17)

其中，tr为标志视认时间(单位：s)．

3.1.2 决策距离Ld

驾驶员在认读标志后，需要根据自己的需求结合标志内容判断决策采取措施．根据相关研究[16]，决策时间td为

td=1.237 554e0.258 913x

(18)

其中，x为信息容量(单位：bit)，1 bit的信息容量相当于从2个相同概率的反应中选择1个所需的信息处理量．

需要驶离主线驾驶员从驶离和不驶离这两个情况中做出选择，相当于1 bit的信息容量，故决策时间为1.6 s，此时车辆匀速行驶，则

(19)

3.4 车辆换道距离L4

车辆换道距离和车辆重新分布的过程相同，当车辆实施换道时，考虑最不利情况，即最内侧车道车辆需要换道至最外侧车道驶离主线，根据换道次数与类型的不同，所需的车辆换道距离具体见表4．

表4 不同情况车辆换道距离Table 4 Lane changing distance under different conditions

3.5 安全确认距离L5

驾驶员完成换道后需要有足够的确认距离，使驾驶员识别主线出口的分流点和分流鼻，此段距离称为安全确认距离．结合相关研究[17]，本研究取确认时间2.5 s，此时车辆应匀速行驶，则安全确认距离为

(20)

其中，L5为安全确认距离(单位：m)；t5为确认时间(单位：s)．

3.6 出口减速段距离L6

出口减速段包括出口渐变段、辅助车道及变速段，由于主线上的出口减速段与出口匝道的减速车道相同，且出口渐变率较小，减速车道线形与主线一致，故可认为主线出口减速段近似长度等于减速车道长度．根据《细则》规定，出口减速段距离具体见表5．

表5 出口减速段距离Table 5 Deceleration lane distance

3.7 主线相互合流至主线出口的最小间距L

主线相互合流至前方主线出口的最小间距L为

L=L1+L2+L3+L4+L5+L6

(21)

在不同的设计速度下，考虑最不利情况，对于不同的主线相互合流方式、车道数及换道类型，主线相互合流至前方主线出口的最小间距建议值见表6(按10取整)．

表6 主线相互合流至前方主线出口的最小间距Table 6 The minimum spacing between the mainline mutual confluence and the mainline exit

4 VISSIM仿真验证

限于篇幅，本研究通过VISSIM仿真平台，选取单车道出口的3+2-1=4型的最小间距建议值进行仿真验证．根据改扩建后的广东佛开高速基本参数作为输入参数：佛开高速设计速度为120 km/h的单向4车道高速公路，行车道宽3.75 m；年平均日交通量达100 000 pcu/d，根据相关参数换算得设计小时交通量为5 100 pcu/h，作为主线相互合流后的交通量；其中，小型车占60%，大型车占40%；主线相互合流前左侧交通量占60%(3 060 pcu/h)，右侧占40%(2 040 pcu/h)；综合考虑取主线出口驶出交通量占15%(765 pcu/h)．

同时选取交互状态、仿真时间及车辆编号作为配置参数，在保证交通流稳定性的前提下，选取记录时间为600～4 200 s；选取高速公路(随意选择车道)作为驾驶行为参数，对车辆换道模型中的参数进行标定；根据驾驶员的驾驶行为和心理特征，在仿真模型中增加车辆输入模块及车辆决策点，增加仿真的真实性．

选取冲突率作为评价指标，通过VISSIM仿真，得到不同间距下的冲突率见表7，不同间距与冲突率关系如图7．根据相关研究[18]，将道路路段安全水平分为4类： 安全、 较安全、 临界安全及不安全，运用SPSS软件对仿真数据进行迭代聚类，得到4个聚类中心，并对冲突率进行模糊隶属度评价．

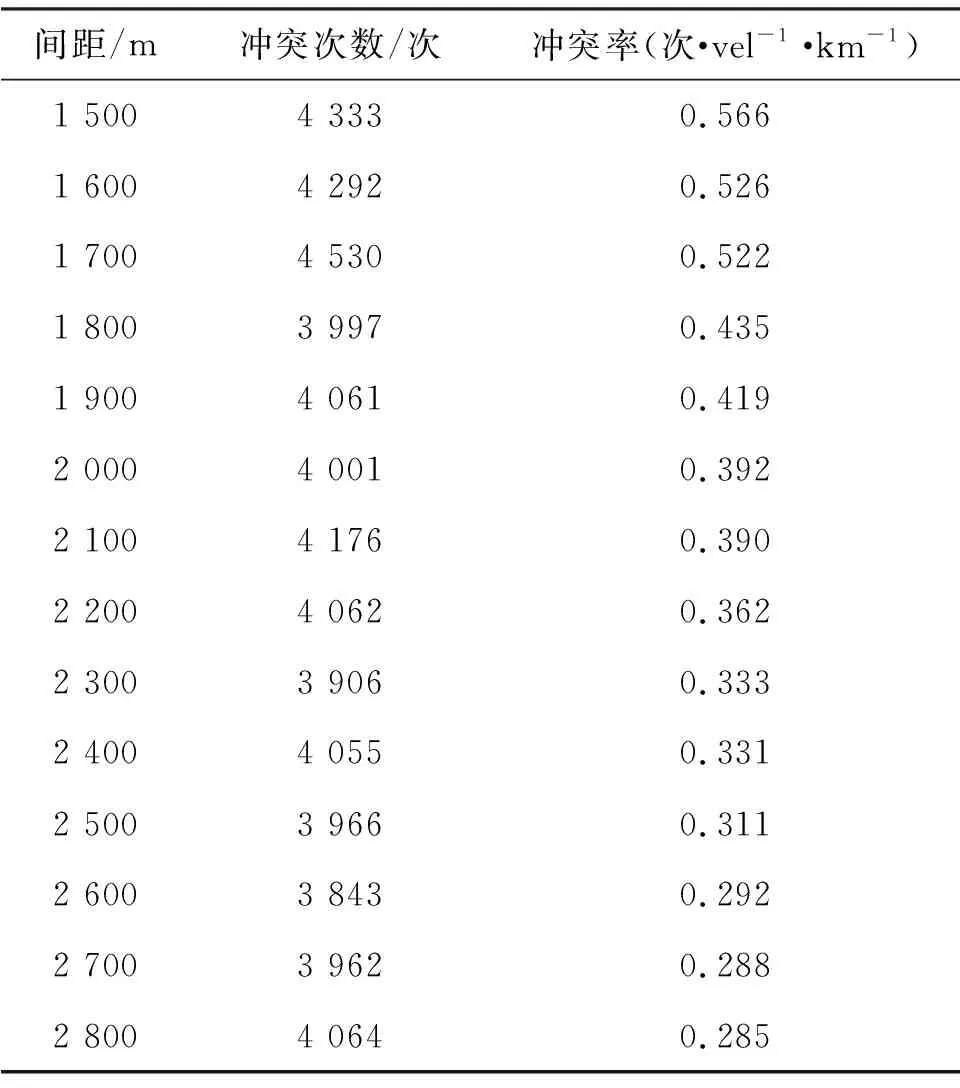
表7 不同间距下的冲突次数及冲突率Table 7 The number of collisions and the conflict rate under different spacing

图7 不同间距与冲突率的关系Fig.7 The relationship between different spacing and conflict rates

对设计速度为120 km/h单车道出口3+2-1=4型的最小间距建议值进行仿真可知，当且仅当最小间距大于等于建议值时，其冲突率满足模糊隶属度评价，道路安全水平为安全．由图7可见，当间距小于建议值时，随着间距的增大，冲突率急剧降低；当净距大于或等于建议值时，随着间距的增大，冲突率的下降趋于平缓，故仿真验证结果与上述最小净距模型计算建议值相符合，证明了最小净距模型和最小净距建议值的合理性．

结 语

本研究首先明确了主线相互合流至主线出口之间的间距的定义，研究分析不同主线相互合流方式、换道类型及车道数对间距的影响；其次，从安全角度出发，建立主线相互合流构造距离计算模型；通过研究不同的主线相互合流方式、换道类型及车道数，考虑主线相互合流的交通流特性和车辆换道特征，建立高速公路主线相互合流至主线出口的最小间距计算模型；通过对最小间距计算模型相关参数的分析，提出高速公路主线相互合流至主线出口的最小间距建议值．

由于我国现有规范没有给出相应建议值，本研究可为设计人员提供参考；但车辆换道模型中的可插入间隙有较多算法且影响因素较多，仅理论分析略显单薄，需通过实验以得到等待可插入间隙的时间．