基于改进KMC算法的三相交通流聚类研究
2018-11-20王全
王 全
(广州千陌互连科技股份有限公司,广东 广州 467000)
0 引 言
为了更好地解释交通流状态转变中表现的特性,德国学者Kerner在总结和研究了大量交通流经验数据的基础上提出了三相交通流理论[1-4],并进行了扩充和完善[5]。不同于经典的两相(自由流和拥堵流)交通流理论,该理论认为交通流状态存在三相性,即自由流(Free FLow,F)、同步流(Synchronized FLow,S)和宽运动堵塞流(Wide Moving Jam,J)。近年来,国内外学者基于三相交通流理论提出了许多相关研究成果。Jia等[6]提出了基于三相交通流理论的元胞自动机模型,在考虑周期和边界等条件下,对同步流的基本图特性及入口匝道导致的不同拥堵模型进行了深入研究。Tian等[7]利用基于交通流基本图的元胞自动机对三相交通流理论的影响进行还原分析。Rehborn、Schafer及Hermanns等分别利用各自的交通流数据样本对交通流转变过程中的三相状态进行验证和分析[8-10]。
三相交通流理论从交通流运行过程中的数据特性入手,假设交通流状态转换包括F→S,S→J和F→J,并认为F→J无存在的可能性[4],因此主要的研究难点在于如何清楚地确定F,S和J的边界[11]。为了解决该问题,本文将应用KMC算法对交通流数据进行相关聚类分析,研究三相交通流的参数区间并得出结论。
1 相关算法及理论
1.1 改进的K均值聚类分析算法
KMC(K-means Clustering,KMC)算法是最经典的聚类算法之一,因其具有思路简单、聚类快速、局部搜索能力强的优点而被广泛应用。设聚类样本将其划分为多个不同的类别为d维向量,k为聚类中心个数。聚类中心计算公式如下:
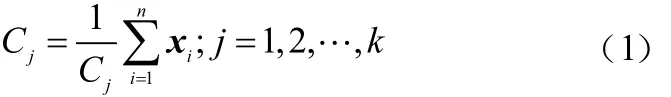
KMC的准则函数如下:
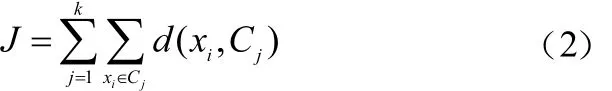
式中:d(xi,Cj)表示数据xi与所属聚类中心Cj的欧式距离;J表示类内所有点到类中心的距离之和。KMC的聚类思想即找到一组类中心,使得类中其他点到达本类中心的距离之和最小,即J最小。
KMC的一个缺点是容易陷入局部最优,因而对初始聚类中心的选择非常敏感,本文应用如下算法对聚类中心的初始化进行改进,避免KMC陷入局部最优。聚类中心初始化算法流程如下:
(1)设聚类中心集合为C,在数据序列中随机选择一个加入C;
(2)计算所有数据点到C中点的距离,将距离最大的点作为新的聚类中心并加入C;
(3)重复步骤(2),直到C中的聚类中心数量达到要求;
(4)返回C作为KMC算法的初始聚类中心。
1.2 信息熵及其跃迁值
1948年,C.E.Shannon将熵概念引入信息理论,用信息熵来度量数据所含的信息量,其表达式定义如下:
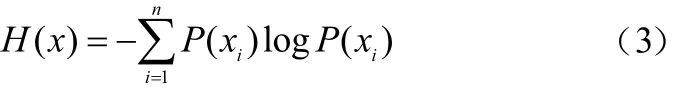
式中:xi代表信源端各不同的信号;P(xi)表示信源中每个信号出现的概率;H(x)表示信源总体信息量的统计平均值。因此,将序列划分为K个类集合,则x的总体信息熵为:

值得说明的是随着聚类个数的增加,每个类中的数据量减少,每个数据属于一个类的概率增大,该类总体的信息熵就变大。在类个数由少增多的过程中,类划分按无序→有序→无序的顺序进行,最初的无序是因为聚类太笼统,看不清数据集的特征,而最后的无序是聚类太细碎,缺少总体认识。因此,可以用数据集总体信息熵的跃迁值来确定最佳的聚类数目[12]。如果当聚类数量从n增加到n+1,总体信息熵值跃迁值很小,则说明将数据集划分为n个类比较合适,没有再增加类中心的必要。本文中,我们将利用信息熵的概念及其不同聚类数目变化幅度对聚类分析的结果进行探讨。
2 数据样本简介
本文所用的交通流数据均采集于广州市广园快速路在五山路出入口的上下游路段,为了着重分析连续交通流的三相特性,选取2016年8月22日(星期一)工作日数据作为分析样本,其时间样本如图1和图2所示。由交通流时间序列分布可知,下游路段由于受到出入口的影响比较显著,速度和占有率在时间上的变化较上游路段稍显混乱,下文中将进行详细分析。
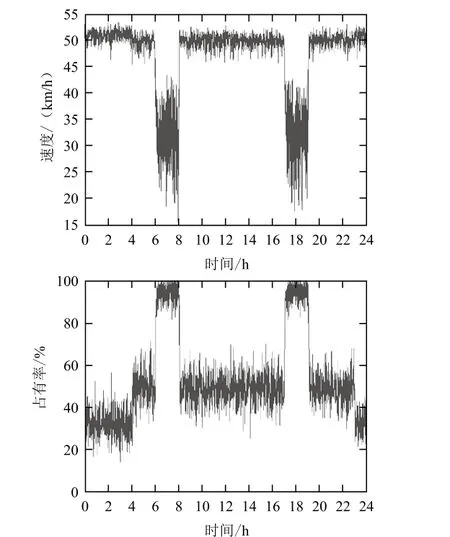
图1 上游路段交通流时间序列
3 基于改进K均值算法的交通流聚类分析
3.1 基于信息熵跃迁值的聚类数目确定
对交通流时间序列进行聚类分析之前,必须先确定最优的聚类个数,使得聚类数据包含的信息量最大。以交通流速度-占有率关联分布为例,不同的聚类数目会有不同的聚类效果,数据集的总体信息熵会不断变化。图3所示为速度-占有率聚类数目由2~4个的聚类结果,图4所示为不同聚类数目信息熵跃迁值的变化结果,由此可知,聚类数目由2增加到3时,信息熵跃迁值降到最低,而由3到4的过程信息熵的跃迁值反而增加,说明有3个聚类中心时交通流时间序列的总体信息量最大,该结果与三相交通流一致。
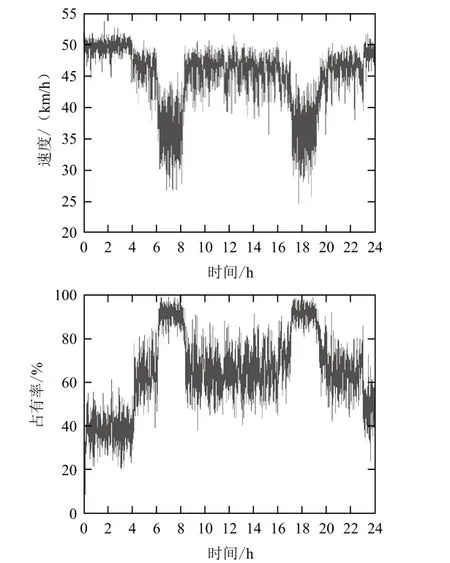
图2 下游路段交通流时间序列
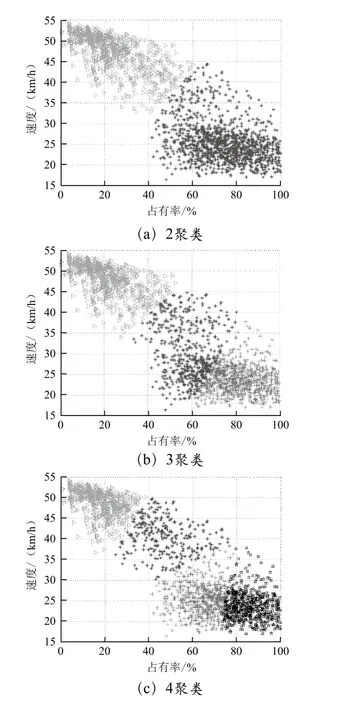
图3 速度-占有率分布聚类结果

图4 信息熵跃迁值变化
据上所述,从三相交通流及信息熵总量来看,将交通流分为3类时包含的信息量最大。对交通流速度时间序列、占有率时间序列进行分别聚类,可以发现交通流不同状态的边界,为交通流状态判别提供数据支撑。
3.2 交通流时间序列聚类分析
以数据样本中上游路段为例,速度时间序列和占有率时间序列的聚类分析结果如图5所示。可见,聚类算法能够准确识别出高峰流量区间,并分出各交通流状态的边界。该路段设计时速为60 km/h,实际情况下自由流平均速度约52 km/h,同步流速度在31~43 km/h之间,低于30 km/h时,交通处于拥堵状态。对应的占有率分别为0~42%,43%~74%,74%~100%。

图5 上游路段交通流时间序列聚类结果
4 上下游路段交通流的聚类对比与分析
4.1 交通流聚类结果对比
综合上游路段的交通流时间序列的聚类分析结果与下游路段受出入口的影响,交通流时间序列更加复杂,其聚类结果如图6所示。相比上游路段,下游路段的交通流分布稍显混乱,从聚类结果来看,各状态的速度和占有率区间发生了变化,具体见表1所列。
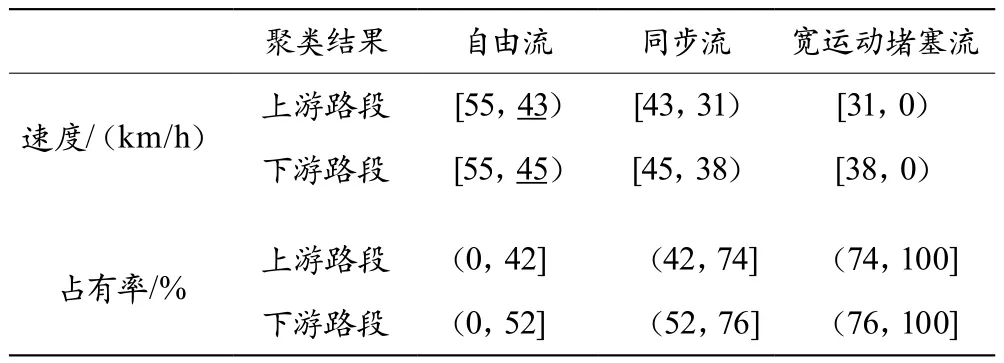
表1 上下游路段交通流参数聚类区间对比
由表1可知,两个路段的自由流速度下界和宽运动堵塞流占有率上界较一致(表中下划线数字),而同步流的速度下界和占有率上界存在较大差别。结合图5和图6分析可知,造成上游路段交通流由S→J转变的主要原因是出入口车辆的干扰,而下游路段不仅存在干扰问题,车流量增大也会导致道路占有率分布总体上浮,但由于前方不存在排队现象,因此交通流的速度也较上游大。无监督的KMC聚类中心的全局最优值取决于数据分布特征,因此两个路段的聚类区间存在差别。

图6 下游路段交通流时间序列聚类结果
4.2 聚类结果的自信息量分析
自信息量是指数据样本中每个点在其所属类中出现的概率,计算公式见式(5)。利用所有数据点与其对应自信息量相乘的分布可以分析聚类结果的成分,进而分析聚类的可靠性。

图7所示为上游路段聚类结果的自信息量分布,从中可以看出,速度时间序列的聚类结果中在自由流状态时只有一种成分,另外两个状态则可能出现不同的速度值;同样,占有率时间序列的聚类结果中,拥挤流也只包含一种成分,另外两种状态亦不然。由此说明,高速度的交通流只在自由流状态时出现,同步流和堵塞流时速度变化区间较大;高占有率的交通流只有堵塞流才会表现出来,自由流和同步流状态可能会出现瞬时的占有率浮动。故而在交通流时间序列的聚类结果中,自由流速度区间的下界和拥堵流状态占有率区间的下界识别结果较可靠,也从另一个角度说明了上下游两个路段聚类结果中这两个值较为一致的原因。
5 结 语
本文基于改进的KMC算法,利用信息熵的跃迁值确定交通流时间序列的最优聚类数目,在此基础上分别对上下游两个关联路段的交通流时间序列进行聚类分析,根据数据的自信息量分布对聚类结果进行分析。从本文的研究中可得出以下结论:
(1)交通流时间序列的聚类分析从数据角度证明三相交通流理论适合于交通流状态的判别研究;
(2)聚类分析结果证明交通流在F→S的状态转变中,以速度为判据更可靠,而在S→J的状态转变中,以占有率变化作为判据更可靠;
(3)交通流数据的聚类结果因路段道路条件、交通流组成的不同而存在差异,应结合具体的数据分析给出合理的状态判别。
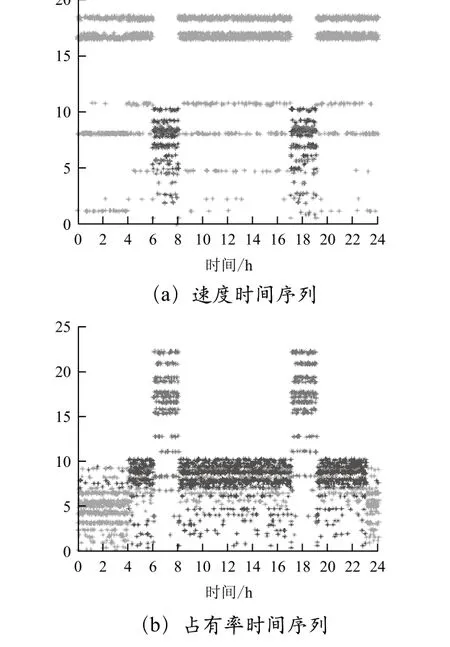
图7 聚类结果的自信息量分布
