关于定积分计算方法与技巧的再补充

马艳丽，褚正清，李海霞，聂东明

（安徽新华学院通识教育部，安徽合肥230088）

高等数学微分学中的一个重要部分就是定积分的概念和计算，教学的重点就是熟练地掌握定积分的计算，它也是教学中的一个难点。在学习定积分的计算中，最重要的是掌握它的运算方法与应用技巧。定积分计算中常用的计算方法有基本性质、基本公式、换元积分法和分部积分法，简单的还有定积分的几何意义、利用函数的奇偶性和查积分表等[1-2]。但有些定积分的计算需要一些特殊的方法与技巧，这样可以大大减少计算时间，提高运算效率。本文从另外9个方面对定积分的计算方法与应用技巧进行了补充和探讨，并结合相应的例题给出每种方法的解题思路，以更好地掌握和应用这些方法，从而达到费力小、收效大的学习效果。

1 利用方程式计算积分

在计算过程中，有时需要通过换元积分和分部积分等列成一个方程或方程组进行求解定积分。

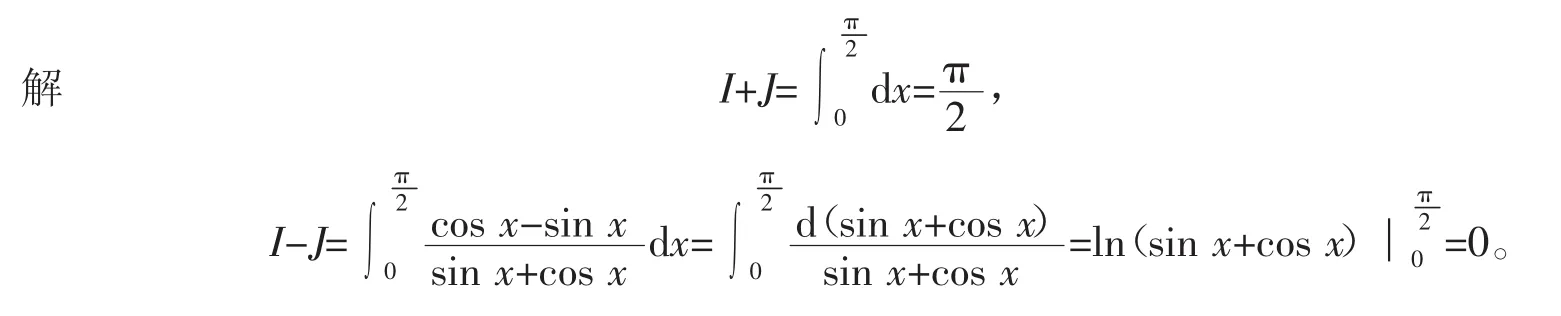
2 利用消项法计算积分

对于某些不易计算的定积分，在通过一系列变形之后，积分的某些部分相互抵消从而得到它们的值。对于定积分，一种计算方法一般情况下只能尝试着去使用。

3 利用反函数法计算积分

定理1[3]若函数f（x）在闭区间[a，b]上连续且是严格单调的，其反函数是，则

定理2[3]设函数f（x）在闭区间[a，b]上可积，若f（x）在[a，b]上存在反函数，函数g（x）在闭区间[a，b]上可积且存在原函数]上可积，则

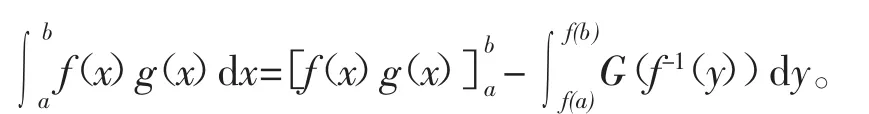
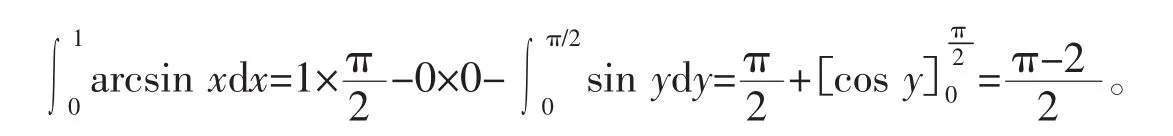
解 令f（x）=ln x，则f（1）=0，f（e）=1，其反函数为。

再令 g（x）=x8，它的一个原函数为，则，根据定理 2 知

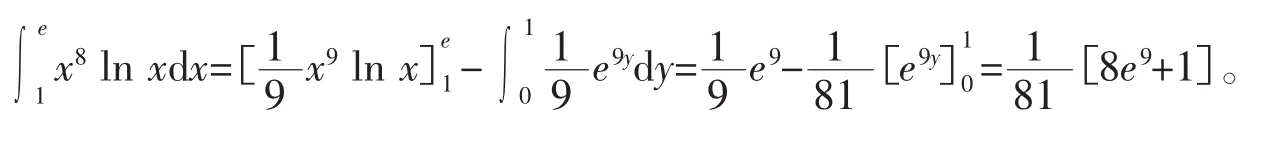
4 利用二重积分计算积分

对于二重积分的概念，需要进行逆向思维，对于某些定积分，可以先转化成二重积分，然后再进行运算。

5 利用定积分的有关公式简化计算积分

在一些特殊情况下，运用一些特殊的公式和技巧可以使定积分的计算大大简化，并且可以提高学生学习的积极性，引导他们进行积极思考，例如[4-6]：

（1）若函数f（x）在[a，b]上连续，则：

6 利用变量代换计算积分

对于一些定积分，其被积函数的原函数是非初等函数，所以用牛顿莱布尼茨公式不能直接计算，但可通过变量代换来求值计算积分值[7]。变量代换在定积分的计算中很常见，有根式代换、倒数代换等，技巧性比较强，解无定法。

7 利用导数计算积分

8 利用递推公式计算积分

利用递推公式计算定积分，此种方法比较常用，在许多课本中都有所介绍。特别地，当被积表达式中包含自然数时，这种方法更加有效。

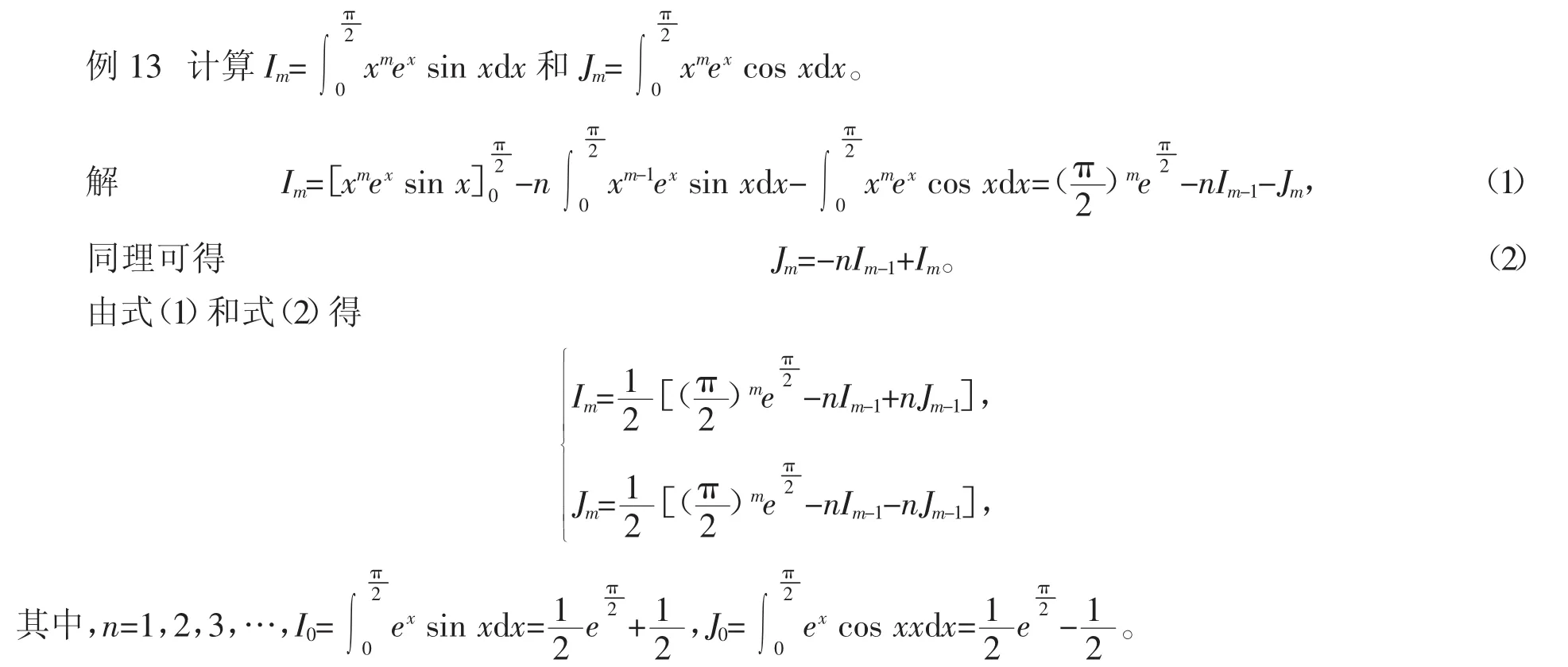
9 利用含参变量的积分计算积分

在定积分的计算过程中，偶尔可以将参变量引入到被积函数中，再根据相关的性质来计算定积分。用此种方法计算时，涉及到的理论知识比较多，比如一致收敛性等内容，技巧性也比较大，使用时要注意条件。

如何学好定积分及其计算方法，这是初学者对于积分学内容首先要面对的问题。本文详细介绍了高等数学中求解定积分的一些常用方法及解题技巧，正确使用这些方法可以使定积分的计算更加简单、容易。