基于Muskingum-Cunge法的河道水位流量预报研究

包红军，王莉莉，李致家

(1.国家气象中心，北京100081；2.河海大学水文水资源学院， 江苏南京210098)

0 引 言

河道水流演算水力要素属于三维非恒定的水力学问题[1]。考虑到三维非恒定的水力学模型基本方程理论假设与数学求解问题，在生产实际作业中往往概化为一维非恒定流模型[2- 6]。圣维南方程组是描述一维水流非恒定流运动的基础方程，水位模拟与预报精度较高；但其对资料，特别是断面资料要求较高，计算繁琐，且目前尚无法求出解析通解，其近似概化模型有运动波、扩散波等[7]。其他用于河道洪水演算方法还有滞后演算法等经验方法、线性水库法、非线性水库法和Muskingum法，其中以Muskingum最为常用[8]。

Muskingum法是实际生产中常用的集总式河道演算方法，由于在河道洪水演算中的简便性和广泛的适用性，其参数确定方法也多种多样。最初的Muskingum法参数槽蓄系数K和权重因子x的确定方法是试错法[1-2]。为了克服试错法计算量大和主观性过强的缺点，有学者采用最小二乘法推导出参数K和x的计算公式[9]。另外，Singh对Muskingum法参数确定的方法归纳为：最小二乘法或者图解法、矩阵及累积量法、直接试解优选法[10-11]。最优化方法实质上属于“黑箱子”模型，难以保证K和x的物理意义[12-13]。1969年，Cunge证明了Muskingum法是扩散波的二阶近似解，将Muskingum法与水力学中的扩散波联系起来，提出Muskingum-Cunge法；另一方面，其形式与Muskingum法相同，但有明确的水力学意义[14-15]。

本研究以淮河中游河道为例，对Muskingum-Cunge法参数进行基于河道流量演算中的经验关系推求，并且结合水文水位法、扩散波非线性水位法，改善Muskingum-Cunge法不能模拟水位的问题，形成基于Muskingum-Cunge法的河道水位流量预报模型，在淮河干流河道洪水预报中进行验证，以探讨减少方法对资料的依赖程度。

1 基于Muskingum-Cunge法的河道水位流量预报模型

1.1 Muskingum-Cunge参数推求

Muskingum-Cunge法中参数K表示洪水波在河段长为ΔL中的传播运动历时，假定洪水波运动速度为VW，则K可由下式计算[16-17]。即

K=ΔL/VW

(1)

1989年，Wilson和Ruffini研究得到：对于某个特定矩形、三角形和抛物线河道断面，其波速VW分别是断面平均波速Vav的5/3、4/3和11/9[17]。而根据曼宁公式断面平均流速[18]

(2)

式中，n为曼宁糙率系数，无因次；R为水力半径，m；S为水面比降，m/m。由此可见，当推求出R值，即可得到断面平均流速Vav。式(2)可写成[19]

(3)

式中，A为断面的过水面积，m2；Q0为参考流量，m3/s(Reference Discharge)。Q0值求解根据文献[17，19]，采用式(4)来求解某场洪水中的Q0。即

Q0=Qm+0.5(QP-Qm)

(4)

式中，Qm为过程最小流量，m3/s；QP为过程洪峰流量，m3/s。

对于给定流量过程可以用公式(4)来推求Q0。糙率n和坡度S分别取自河道地形资料。Punmia和Pande[20]在1981年研究得出在自然流域中湿周与流量的经验关系。即

(5)

式中，P为湿周；c为系数，值域在4.71～4.81。宽浅河道时，可认为P等于过水断面的水面宽W。

抛物线型断面面积可近似按下述公式计算[18]

A=2yW/3

(6)

式中，y为水深。对于抛物线型断面水力半径可以根据Koegelenberg在1997年研究成果[21](见表1)计算

R≅d=2y/3

(7)

式中，d为平均水深，m。

表1 水力半径与水深经验关系

将式(5)、(6)代入式(3)，可得

(8)

因为湿周P在宽浅河道中可近似为水面宽W，所以抛物线型断面的水深

(9)

同理可得到当断面形状为矩形时的水深

(10)

以及当断面形状为三角形时水深

(11)

根据表1可得到各种河道断面形状的水力半径R，代入式(11)求得Vav；同时，也得出Vav是坡度S单调增函数，随着S的增加而增加的结果；进而，根据河段长度由式(1)确定K的值。

Muskingum-Cunge法参数x根据1993年Fread[16]提出的公式计算。即

(12)

1.2 考虑行蓄洪区的Muskingum-Cunge法

河道洪水预报包括流量演算法和水位计算法。行蓄洪是通过流量的变化(分洪、蓄洪)来影响水位的。因而只要在流量演算时考虑行蓄洪的影响即可。以河段[i，i+1]为例，见图1。

图1 河段[i，i+1]概化示意

Muskingum-Cunge法递推公式为

(13)

根据图1，考虑行蓄洪区时，i断面入流包括4个：①支流汇入Gi；②行洪分流出入流(分左右两侧)QFli，QFfi；③蓄洪入流(分左右两侧)QSli、QSfi；(4)[i-1，i]的来水量；则

(14)

(15)

考虑行蓄洪区的Muskingum-Cunge法递推公式

(16)

行洪区与蓄洪区处理方式采用文献[22]的做法：行洪区进行一维河道洪水演算，蓄洪区一般有闸控制，不进行水流演算。

1.3 基于柱蓄和楔蓄的水文水位法

设定1-1为初始水位，2-2为变化后的水位(见图2)，则河道槽蓄量增量

dW=BLdZ下+BLX1(dZ上-dZ下)

(17)

(18)

图2 柱蓄和楔蓄示意

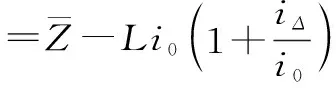
(19)

式中，i0为河道河底比降；iΔ为水流附加比降。

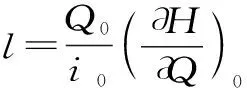
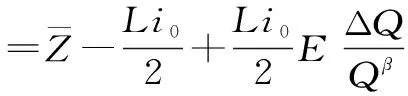
(20)

与Muskingum-Cunge法联解，实现断面水位推求如下

(21)

(22)

(23)

(24)

(25)

1.4 扩散波非线性水位法

利用基于柱蓄和楔蓄的水文水位法与Muskingum-Cunge法联解求得逐段流量和边界水位后，可采用圣维南方程组中的动量方程求解水位[22]。在淮河干流，惯性项相对较小[7]，可忽略去惯性项，得到

(26)

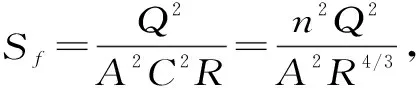
(27)

以θ为差分因子，应用四点隐式差分格式，得

(28)

再利用迭代计算推求河道断面水位。

2 基于Muskingum-Cunge法的河道水位流量预报模型应用分析

本次研究以王家坝水文站至鲁台子水文站的淮河干流为试验河段。河段右岸有史河、淠河两个支流汇入，并且还有两个蓄洪区(城西湖蓄洪区、城东湖蓄洪区)；左岸有颍河一个主要支流汇入，另外还有洪河分洪道、谷河和润河汇入和蒙洼蓄洪区、姜唐联湖蓄洪区、南润段、邱家湖、润赵段三个行洪区。王家坝至鲁台子河段共有三个水文站与四个水位站，在整个流域防汛中，一直处于洪水预报关键之处[24-26]。

王家坝至鲁台子河段全长155.16 km。根据王家坝～鲁台子河道水利工程的位置、支流的汇入位置、水文站水位站的位置和行蓄洪区位置情况，河段共分10段。

选取淮河1996年至2008年汛期洪水资料进行检验。14场洪水均取得较好的模拟效果。为了能使Musking-Cunge能够模拟好大洪水时干流洪水顶托作用，支流延后至退水期再进入干流的洪水过程，故假设在支流洪水进入干流之前，存在一个线性水库，即支流洪水需要经过一虚拟线性水库调蓄后方能进入干流。对于综合法而言，当河道比降大时，属于运动波，用水文水位法提供上边界水位条件，而当河底比降小时，属于扩散波，用水文水位法提供下边界条件。前者用扩散波非线性水位法从上游向下游推求其他断面的水位，后者用扩散波非线性水位法从下游向上游推求其他断面的水位。淮河干流河道比降较低，因而采用扩散波非线性水位法自下游向上游推求水位。通过在1996年至2008年洪水的检验，该处理方式具有一定的效果，使得洪水的模拟精度得到了提高，如表2所示。

表2 王家坝至鲁台子河段洪水模拟结果

注：y表示行蓄洪区使用年份；①为实测最高水位减去计算最高水位；②为计算与实测水位过程拟合的确定性系数；③为计算洪峰流量的相对误差；④为计算与实测流量过程拟合的确定性系数。

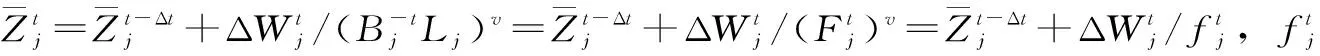
3 结论与讨论

本次研究对Muskingum-Cunge法参数进行基于河道流量演算中的经验关系推求，并且结合基于柱蓄与楔蓄的水文水位法、扩散波非线性水位法，改善Muskingum-Cunge法不能模拟水位的问题，建立基于Muskingum-Cunge法的河道水位流量预报模型。通过在淮河干流河道洪水模拟中验证，效果较好。

(1)Muskingum是根据实测洪水资料优选参数，行蓄洪等水利工程以及河道洪水自身特性等对河道洪水的影响可以在优选出来的参数值中反映出来，而Muskingum-Cunge法的参数完全根据水力要素推求，没有考虑到分洪、漫滩等等，推求出来的参数不能反映水利工程和河道自身水流特性等等因素的影响。这是Muskingum-Cunge法在下一步研究与实际生产应用中需要解决的问题之一。

(2)为了实现Muskingum-Cunge法模拟水位，Muskingum-Cunge法与基于柱蓄与楔蓄的水文水位法、扩散波非线性水位形成基于Muskingum-Cunge法的河道水位流量预报模型，方法的优点在于不依赖洪水历史资料，参数完全基于河道物理特征求得。为了提高水位模拟精度，应用实时校正模型，利用当前的预报误差，建立对系统模型与预报的现时校正的回馈机制，是提高精度的重要手段[7]。

对于复杂的分叉水系及分红、溃口、溃坝等的洪水预报，或者在计算河道内兴建了水利工程或者河道特征发生了明显变化后，需要计算和预报河道内任何断面任何时刻的水位、流速、流量等要素时，这时水动力学方法仍是首选[6，25]。