浅谈地铁车辆排班问题

李成坤，王丽娟

（西南交通大学希望学院，四川 成都 610400）

随着城市经济的快速发展，城市轨道交通系统对于人们的出行扮演着越来越重要的角色。在地铁车辆资源有限的情况下，合理的编排地铁车辆的行车计划成为地铁公司亟待解决的问题。文章主要研究轨道车辆排班，建立了关于高峰时间段的0-1整数规划模型、地铁公司最小经济损失的模型，通过最小损失、单程时间、发车间隔，得到相应的排班和车辆数。同时在此基础上进一步深化，优化误差，添加约束条件，将多目标优化转化为单目标优化。最终求出地铁完成一整天的运行所需要车辆数、排班。

1 排班计算

计算一天地铁车辆排班问题，从四个时间段计算，早高峰时段、日间平峰时段、晚高峰时段、晚平峰时段。

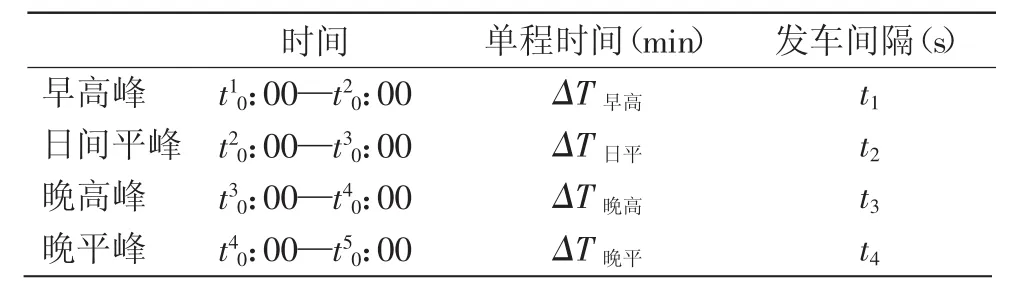
表1 地铁车辆不同时段、单程时间、发车间隔

在上面的基础上，要求出一整天的运行所需要最少车辆数量，查建立0-1模型。

上午班次由同一个驾驶员驾驶的，查得一天不超过b2个班次的约束条件可写为：

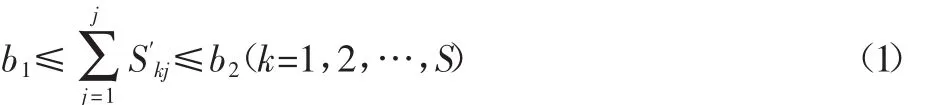
注：b1司机一天最少的班车，b2司机最多班次。

每个班次必须有车辆且车辆数为1的约束条件可写为：

所需最少地铁车辆数为：

每天地铁公司的运营费用为：

其中：μ为地铁每次运行的花费。

对于约束条件乘以加权因子α，查得，将多目标优化转化为单目标优化，最终目标优化函数为：

该算法的终止条件为当遗传代数Gen达到最大规定的最大遗传代数。

由（1）～（5）式子，利用 MATLAB、VisualStudio解得：Ζ。

得到某城市地铁完成一整天的运行所需要车辆数、排班为：

综上可得某城市地铁完成一整天的运行所需要车辆数为：min=|Z0，Z|

2 结语

文章研究了地铁车辆在不同时间段高峰、平峰的车辆运行特性，以达到车辆利用效率最高、最经济为目标，安排车辆的排班调度，从而建立0-1车辆排班模型，得到车辆数和排班，最优调配方案，从而为地铁运营调度提供了必要的理论基础。