遗传算法优化锅炉汽包水位不完全微分PID参数

袁雪峰，马进，强硕，王静

(华北电力大学，河北 保定 071033)

0 引言

锅炉是电力行业重要的能源设备。锅炉汽包液位是锅炉稳定运行的关键参数，液位不稳定有可能引发重大的事故。锅炉汽包水位控制系统，给水量的波动和蒸汽量的波动使液位展现为“正响应特性”，但在蒸汽量急速变大的时候，显现“逆响应特性”[1]，这就是“虚假液位”。引起的原因是当负荷快速变大时，引起汽包中的汽压变小，使水剧烈沸腾，从而导致汽包中的液位提升。

锅炉汽包水位控制系统[2]，是以汽包中液位是否稳定作为标准，通过调节进水量来确保汽包水位稳定在中位线附近，确保锅炉稳定正常运行及工作人员的安全。锅炉汽包水位系统是具有自平衡的控制对象，因为运行过程中有“虚假水位”，使过去的测定方法难以得到正确的参数。汽包水位有着变量多、耦合强、滞后大的特点，本论文设计中将串级三冲量控制与遗传算法结合，将标准PID与低通滤波器结合，设计出遗传算法不完全微分PID控制器来控制锅炉汽包水位的系统，经仿真得出加入遗传算法的PID控制器能够显著提高鲁棒性，达到改善控制质量的效果。

1 常规的锅炉汽包水位控制系统

1.1 锅炉汽包水位的动态特性

确保液位在规定范围之内是保证锅炉正常稳定运行的重要原则之一，液位太高会引起汽包内的蒸汽含水量大，当这种蒸汽进入汽轮机的时候，会对汽轮机造成损害，影响锅炉的安全运行。相反，水位过低，倘若调整不及时就会造成汽包内的水全部蒸发，有可能引起爆炸。所以，要求锅炉汽包水位必须严格控制，锅炉的汽水系统如图1所示。

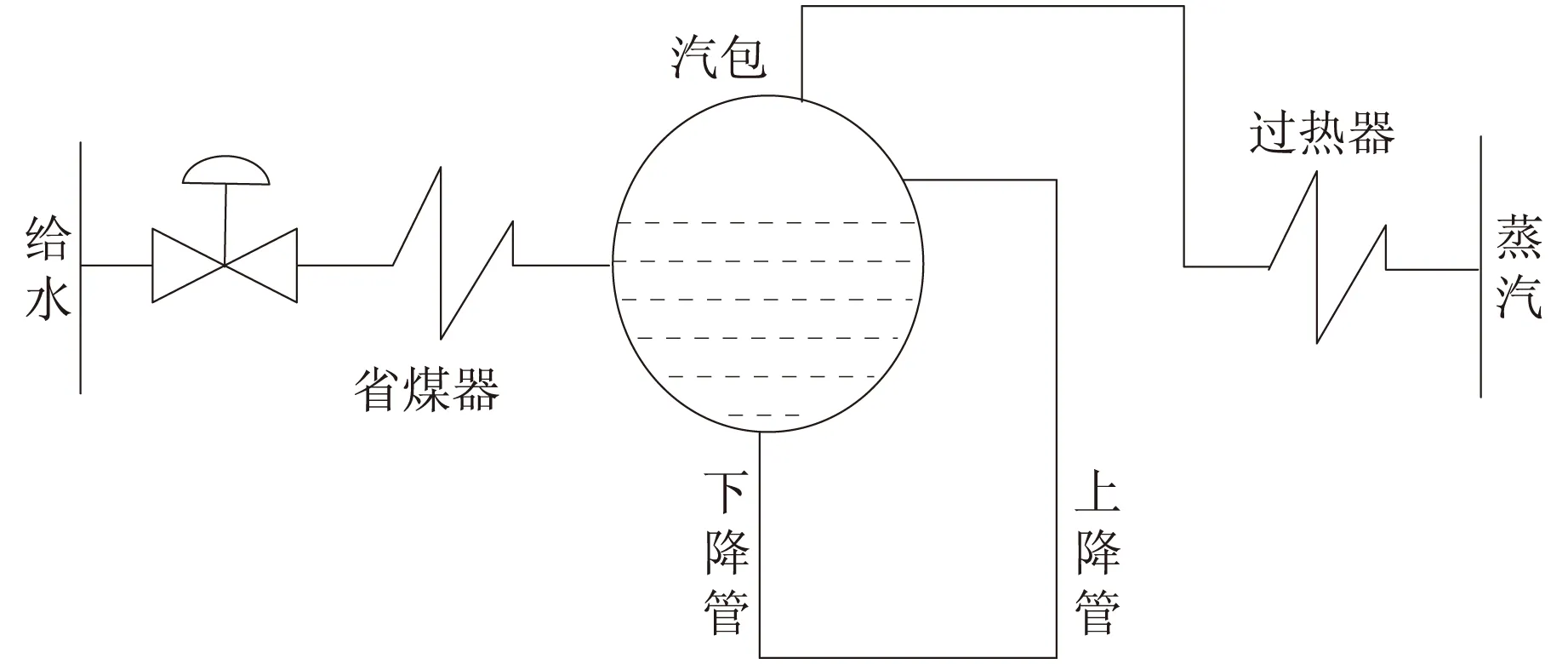
图1 锅炉的汽水系统

在锅炉汽水系统中，给水泵将水送进省煤器来吸收烟道尾部的热量，然后送进汽包。汽包中的水流经下降管到水冷壁，吸收炉内的热量使水蒸发，这时水的状态是汽水混合物，汽水混合物经上升管流回汽包。汽水分离器将汽水混合物的汽和水分离：蒸汽送往过热器继续加热后，最后送往汽轮机；水流回汽包中。

锅炉汽水系统的控制目标是跟随锅炉蒸发量并保证汽包液位在规定范围之内。汽包中的给水是流入，流出是蒸汽。当给水量与蒸汽蒸发流量相等时，水位可以保持稳定。

水位上下波动是因为蒸汽量的波动和给水的不稳定。只有主扰动时汽包水位可用式(1)表达。

(1)

式中：T1，T2为时间常数，s；Tw为给水流量时间常数，s；TD为蒸汽流量时间常数，s；Kw为给水流量的放大系数；KD为蒸汽流量的放大系数；h为汽包水位；vw为锅炉给水流量，kg/s；vD为蒸汽流量,kg/s。

1.2 蒸汽流量对汽包水位影响

蒸汽流量的扰动是外部的负荷变化，是控制系统的外部干扰。如图2所示，当蒸汽流量干扰起作用时，汽包水位H单位阶跃响应。

图2 蒸汽流量干扰下汽包水位阶跃特性曲线

图2中纵坐标D为蒸汽流量，H为汽包液位。其中H，H1，H2分别代表真实液位、物料平衡下理想液位、气泡被干扰的液位。当蒸汽流量增大，锅炉的水位下降，根据物料平衡，如图中H1所示。但事实上由于蒸汽流量的增大，引起汽包中汽压降低。在汽包中，蒸汽用量增加，汽包内水沸腾加剧，汽包容积增加而使水位变化。蒸汽流量迅速增大时，水位会先升高，然后降低，这种现象叫做“虚假液位”。

当负荷改变后，液位以下的汽包体积也发生变化，从而造成水位变化，而且速度非常迅速，图2中H2时间的常数大约十多秒。当蒸汽一侧发生干扰时，汽包中的水位可用式(2)表示为

(2)

式中：kf为响应速度，mm/s；k2为响应曲线H2的放大系数；T2为响应曲线H2的时间常数，s。

“虚假液位”的高低主要受锅炉的工作压力以及蒸汽量影响。例如，一般100～200 t/h的高压锅炉，当有10%的负载变化，“虚假液位”可以达到20～40 mm。

2 不完全微分PID控制算法

在PID控制算法中，微分作用可以改善系统的动态特性[3]。但是，也容易加强高频干扰的影响，当输入信号突变时，微分作用的不足之处就显露出来。在系统中加入低通滤波器可以有效改善这个问题，也就是在PID中加入一阶惯性环节Gf(s)=1/(1+Tfs)，如图3所示。

图3 不完全微分PID控制算法

图3中(a)是将低通滤波直接加在微分环节，(b)则是把低通滤波串在整个PID算法之后，实际两者效果相似。本文针对水位特性，以图3(b)为例进行分析，其传递函数为

(3)

式(3)可表示为

[(1+Tfs)s] ，

(4)

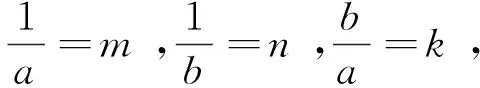
(5)

式中：Tf为时间常数，s；kp，ki，kd为比例常数、积分常数、微分常数。

不完全微分PID控制结构实现的过程中增加了一个开环零点，改善了动态特性。

3 遗传算法的优化过程

遗传算法是一种采用了统计启发式搜索技术的组合优化算法[4]。问题中的每一个解都可以进行编码变成遗传算法可以计算的对象。遗传算法操作过程分为4步。

3.1 参数编码

使用遗传算法处理难题的时候，第一步需要对要求的函数进行编码。遗传算法的算子是对数字串进行计算的。编码原则可以归纳为2点[5]：最有效构造原则；最少字符原则。

遗传算法最基本编码的方式是二进制编码[6]。它具有在交叉操作和其他操作都比较容易的特点。但二进制的编码方式进行二进制和十进制之间数据转换的时候会产生数据转换误差，有可能错过最优点。因此，实数编码方式[7-8]被提出。利用实数编码可以降低编码的长度，减少计算机所需的运算时间。

3.2 初始种群的生成

遗传算法操作的前提是要有一个初始群体，这个群体必须包含许多的初始解。其每一个个体都是随机产生的。使用遗传算子的目的是借鉴自然环境中的进化，对群体中的个体优胜劣汰，得出最好的个体。

3.3 适应度函数

遗传算法在进行参数寻优中只需要适应度函数作为根据，每个可行解都对应一个适应度值可评估群体中个体的优劣。适应度高遗传率大，相反则低。目标函数的值根据它的个体适应度来决定的[9-11]。

3.4 遗传操作设计

遗传操作模拟基因的操作来实现适者生存的进程。参数的寻优搜索是使解逐代地筛选直至逼近解的最优值。

遗传算法一共包括3种算子，分别是选择、交叉、变异。

(1)选择。选择指的是将群体中更好的个体筛选出来构成新一代的种群的过程。选择出来的个体放进配对池中。

每个个体被选中的概率正比于其适应度大小。设群体为M，个体的适应度值是Fi，每一个选择的概率可用式(6)表示。

(6)

(2)交叉。从父代开始交叉，按一定的概率随机选择两个个体进行基因交换，并且交叉的基因位置是随机的，从而产生一个新的个体。这是GA(遗传算法)与其他进化算法不同的重要特征。

(3)变异。变异就是指通过翻转某个基因从而不要快速进入局部最优的陷阱的现象，可以产生新的个体。变异操作有常规位突变、有效基因突变、均匀突变、非均匀突变与零突变等。目前还对许多高级基因操作[12]进行了研发，如倒位操作。遗传算法基本流程如图4所示。

图4 遗传算法基本流程

用遗传算法解决问题时，随机产生初始群体并用适应度函数来筛选，然后选择适应度大的单位进行交叉，并产生新一代群体[13]。对新一代评价、选择、交叉和变异，以提高群体的最佳个体素质，直到最佳个体和群体的平均适应度不再增加或代数运算达到最高，然后结束。算法设计适应度函数作为判断每个可能的解决方案的性能优劣的标准，根据给定的概率，以适应良好的解决方案作为被选定的父代参与遗传操作后，产生新一代的解决方案。

4 优化PID控制器设计

4.1 遗传算法优化PID参数系统

高频干扰往往出现在控制对象和比例-积分-微分(PID)控制器之间，将不完全微分PID控制系统在控制器之后串入低通滤波器可以有效过滤干扰。结合了遗传算法的不完全微分PID控制器进行给水调节，将汽包水位、水流量和蒸汽量3种信号引入，采用遗传算法对三冲量控制系统的参数进行计算。

这个控制系统由2个回路构成：内回路可以消除供水的扰动，使系统更加稳定；外回路是用来减小干扰对液位值产生影响，并保证水位保持在设定值的附近。结合遗传算法的锅炉汽包水位PID调节系统示意如图5所示。

图5 遗传算法优化PID的调节系统

不完全微分控制系统框图如图6所示，在标准PID算法之后串入低通滤波器，形成不完全微分PID控制算法，改善系统的性能。

4.2 基于遗传算法的控制器设计

用遗传算法进行参数搜索的时候更快速，而且在速度和有效性方面效果也很好。将遗传算法用在锅炉水位PID调节的过程中，可以得到甚好的结果。遗传算法控制器系统示意如图7所示。

图8 系统Simulink仿真模型

图7 遗传算法优化的PID控制器系统

图6 不完全微分控制系统框

本文设计的基本思想是：首先把控制器的3个控制参数Kp，Ki，Kd进行二进制编码，再组成一串用来构成一串染色体。随机生成一定数量个体的最初群体，由遗传算法对每一个个体进行操作然后产生新的群体，将新产生的个体再进行适应度评估以及遗传操作，直到满足优化要求。

4.3 PID控制器参数整定

具体的优化步骤如下。

(1)参数编码。参数编码是对PID参数构成的集合进行编码，本文采用二进制多参数编码，二进制编码X与实际值之间有下列关系。

(7)

式中：X∈(Xmin，Xmax)，n为二进制编码长度；M为由二进制位串编码对应的十进制数值。

(2)适应度函数的选择：采用系统偏差作为评估指标。

(8)

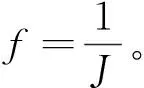
(3)设计遗传算子：采用轮盘赌的选择算子、单点交叉，变异则是常规位突变变异算子。

(4)选取遗传算法的控制参数。遗传算法控制参数有：群体规模M、交叉概率Pc、变异概率Pm。

(5)初始群体生成：使用响应曲线法(Z-N法)得出Kp，Ki，Kd3个参数值，群体是在3个参数值的附近生成的，也是参数寻优的范围。

(6)评价和判定：根据公式计算适应度值，再判断是否可以终止运算。若满足就结束，若不满足则继续进行遗传操作。

5 在MATLAB中的仿真

本文仿真采用某厂120 t/h蒸发量的锅炉为对象进行。锅炉的控制要求是：使蒸汽流量变化保持在-50～50 kg/s范围内，维持水位稳定在-7～7 cm内，阀门输入4～20 mA电流。

给水流量控制器传递函数

G2(s)=0.4 ，

(9)

蒸汽流量与水位之间的传递函数

(10)

给水流量与水位之间的传递函数

(11)

式中：H(s)为水位传递函数；D(s)为蒸汽流量传递函数；W(s)为给水流量传递函数。

取汽包水位设定值为0.3 m，采用MATLAB对该系统进行仿真，并且构建遗传算法的Simulink模型，如图8所示。

确定PID参数，并采用遗传算法进行优化。PID参数确定步骤如下。

(1)经典PID参数的确定采用衰减曲线法，第一步是控制系统只有较大比例，调节出衰减比是0.75的阶跃曲线，得到PID参数为KP=20，Ki=0.51，Kd=0.17。

(2)利用遗传算法程序进行参数优化，确定适应度函数式，设置遗传算法参数对该系统进行PID参数求解：代数为100代；初始种群为40；精度取0.001；交叉概率为0.60；变异概率为0.01。

遗传算法选择方式采用轮盘赌的选择方法；交叉方式采用单点交叉的交叉方法；变异采用常规位突变变异算子；

仿真时间为100 s，采样时间设置为0.3 s，并且在第50 s加100%的干扰。

仿真得到遗传算法PID参数为Kp=42.7，Ki=0.2，Kd=48.7。最终采用衰减曲线法得到的PID与遗传算法PID响应系统曲线以及两者对比如图9所示。

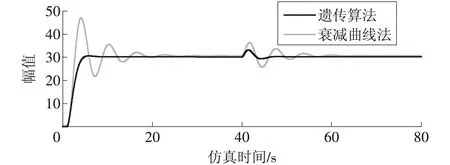
图9 衰减曲线与遗传算法PID控制系统响应曲线对比

从曲线中可以清晰地看出采用了遗传算法的控制器超调量更小，稳态误差很小，调节时间更快，很大程度上弥补了工程整定方法在调节PID控制参数上的不足，能够取得较好的控制效果。

在PID算法之后加入随机干扰，分别对加和不加低通滤波器的两种情况进行仿真，得到仿真结果如图10、图11所示。

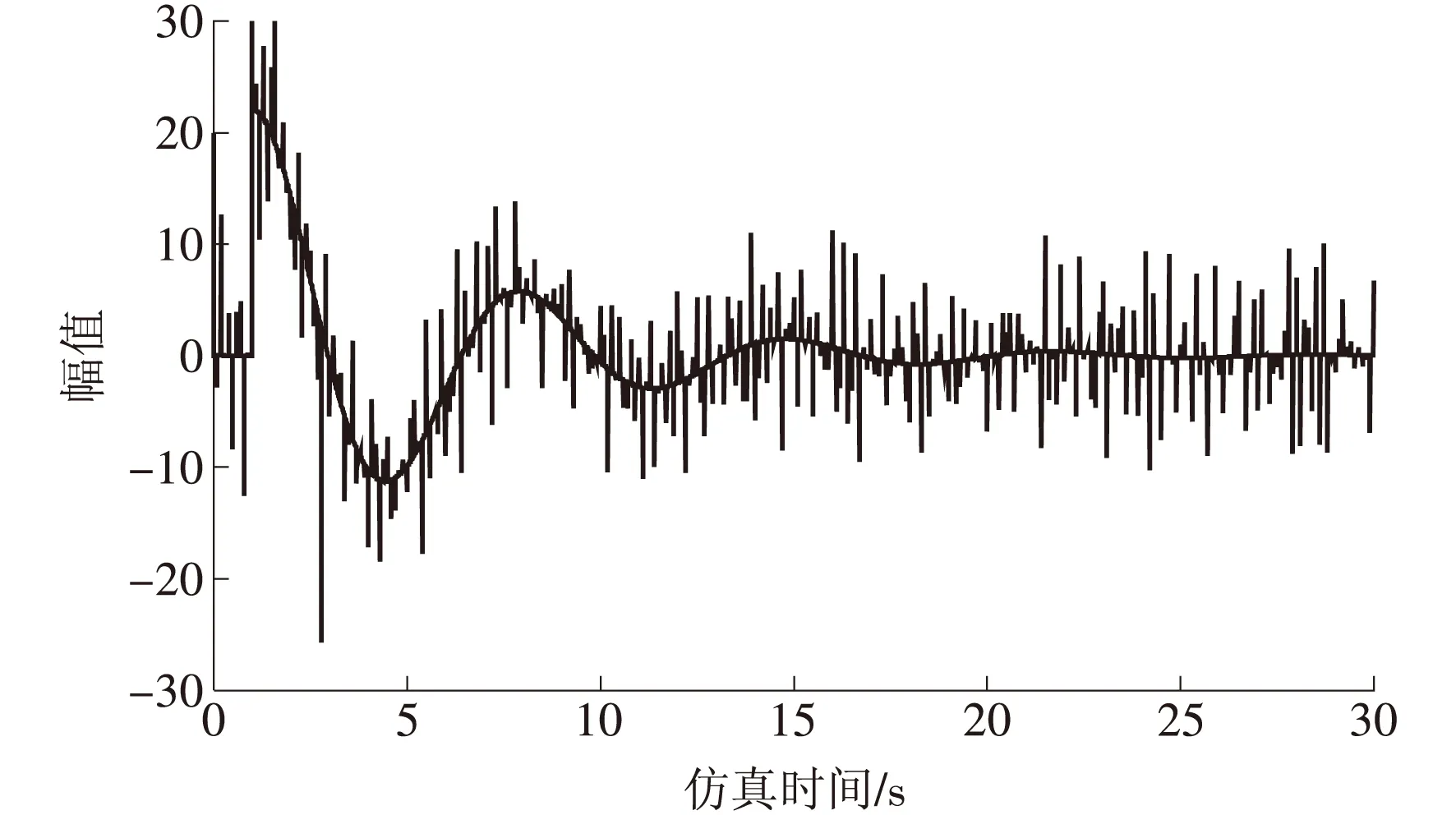
图10 标准PID控制器输出曲线

图11 不完全微分PID控制器曲线

从图10中可以看出，由于微分的作用，高频干扰被放大，因此产生的控制信号受到很大的扰动，动态特性很差，对系统的稳定性产生影响。

从图10、图11中可以看出，不完全微分PID算法可以有效过滤高频干扰，改善系统动态性能，从而让系统稳定。

6 结论

本文将低通滤波器加入标准PID算法，并将遗传算法与常规工程调整PID的方法相结合，在 MATLAB中搭建系统模型，以汽包水位为控制对象，通过仿真可得出，利用遗传算法对参数进行整定，使系统控制效果优于人工整定方法，遗传算法的收敛速度以及超调更为理想。根据定义参数的范围，利用遗传算法可以给出该范围内的最优解，这有利于我们在设计系统的时候可以根据具体的需要来选择对应的参数。不完全微分PID算法可以有效过滤高频干扰，提高系统动态性能，将遗传算法与不完全微分PID相结合可以优化PID参数并让系统更加稳定运行。