基于差动差分电流传输器滤波器的新型综合方法

阮能海

（南京师范大学 物理科学与技术学院，江苏 南京 210023）

0 引 言

差动差分电流传输器（DDCC）是类似于输入端的差动差分放大器（DDA）和输出端的第二代电流传输器（CCII）的一种电路。文献[1-10]提出了几种使用DDCC的通用滤波器。大多数文献中只提出了新型电路，却没有提出基于DDCC的通用滤波器的设计或综合方法。电压模式滤波器的系统综合方法在多数文献中均有报道。然而，这些文献却没有明确指出电压模式滤波器的系统施工方法。

文献[11-15]提出了一种在不需要任何详细电路形式的先验知识前提下实现线性有源电路系统综合的符号化框架。这种叫作节点导纳矩阵扩展方法对于系统地生成各种新颖的电路非常有效。基于这种有源网络的综合方法，文献[16-20]中实现了几种跨导运算放大器、第二代电流传输器、平衡输出逆变电流传输器、差动电压式电流传输器、电流模式和电压模式滤波器的设计。其中，文献[12]中提出的电压模式滤波器的综合过程适用于综合具有不同电路拓扑的不连续传递函数。使用相同的拓扑却很难实现综合多个通用滤波器。文献[16-17]中提出的电压模式滤波器的综合过程适用于综合具有不同电路拓扑的不连续传递函数。文献[18]中报道了基于NAM扩展的跨阻抗滤波器综合。

1 提出方法的描述

为了使用NAM扩展来综合滤波电路，传递函数的分母D(s)在NAM方程式中应表示为导纳矩阵：

理想DDCC的端口关系可以用式（2）来表示，其中加号和减号表示电流传输器为DDCC+或DDCC-。图1和图2显示了DDCC的符号化结构表征。很明显，每个终端Yi（i=1～3）具有高输入阻抗。

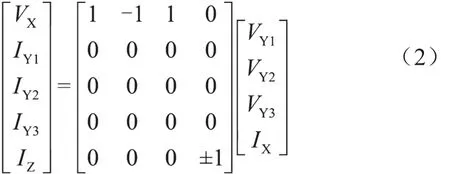
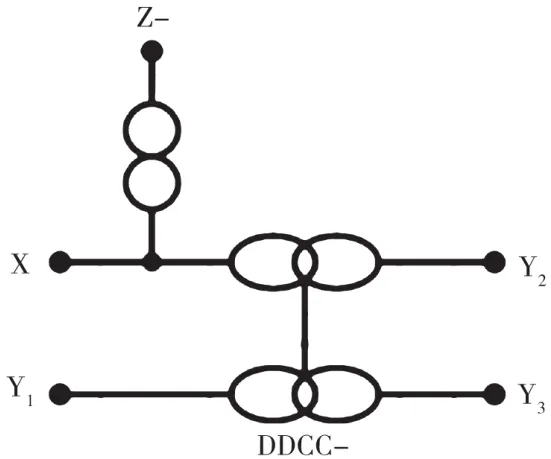
图1 DDCC-的符号化结构表征

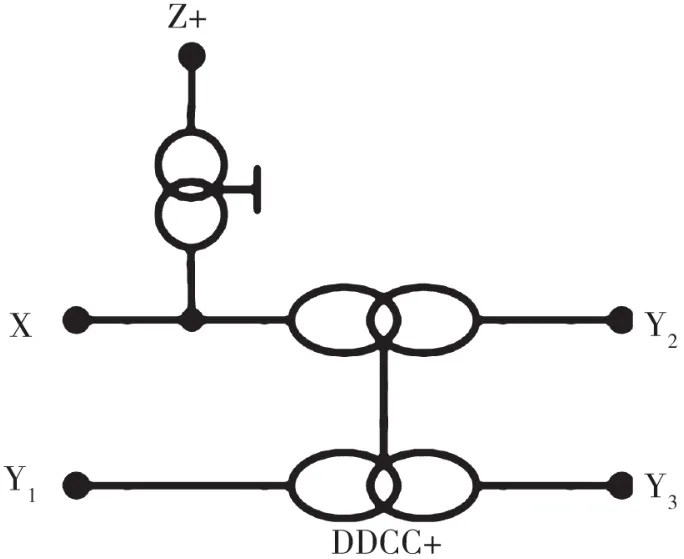
图2 DDCC+的符号化结构表征

在NAM扩展过程中，需要添加在导纳矩阵的主对角线上具有一个公共节点的零项的行和列以及无穷变量项来将导纳项转化为其在导纳矩阵[15]中的正确形式。因此，在综合电路中，可以通过适当类型的CCII[16，21]来实现具有公共节点的奇异元件对。

DDCC类似于CCII，但是具有两个附加的终端，即终端Y2和终端Y3。因此，DDCC-和DDCC+可以分别由在NAM扩展中方程式（3）和式（4）中给出的无穷变量符号来表示，其中主对角线上的公共节点分配给终端X。终端Y1和终端Y3的无穷变量符号和终端X的无穷变量符号是不同的，而终端X和终端Y2的无穷变量符号是相同的。基于式（3）和式（4）中的无穷变量符号可以看出，终端X和终端Y1或终端Y3之间的连接相当于零子（Nullator），而终端X和终端Y2之间的连接相当于电压镜（Voltage Mirror，VM）。这些关系对于推导综合滤波器的传递函数分子非常重要。

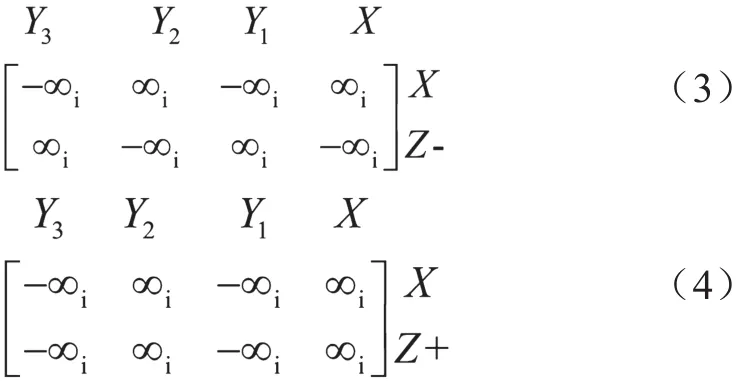
为了使用NAM扩展来综合基于DDCC接地电容的滤波器，首先使用CCII的NAM符号[15]来扩展矩阵（1）中的起始矩阵。矩阵（1）的扩展NAM包括导纳元素的正确形式和DDCC的终端X、终端Z和终端Yi表示的无穷变量对，其余的输入终端可用于注入输入电压源，如图3所示[22]。

图3 电压源的电阻-零极子等效电路

程序可以总结如下。

第1步：以矩阵（1）的形式来排列综合滤波器所需传递函数的分母。必须注意，分母中的每个电容必须排列成在主对角线上只有一个位置，以得到具有接地电容的电路。

第2步：将一行和一列零引入第1行和第1列，将单一电阻放入到矩阵（1）的位置(1,1)。将现有的列和行移动到右侧和底部，如矩阵（5）所示。然后，添加无穷变量和零项，以实现第1列和第2列之间的零子，以及第2行和接地之间的任意子（Norator）。第2步相当于在图3中添加电压源的等效电路。所以，矩阵（5）变成矩阵（6）。

第3步：使用NAM扩展方法来扩展矩阵（6）[12,15]，并使用DDCC方程式的无穷参数表示方程式（3）和方程式（4），得到的矩阵可以用式（7）表示：

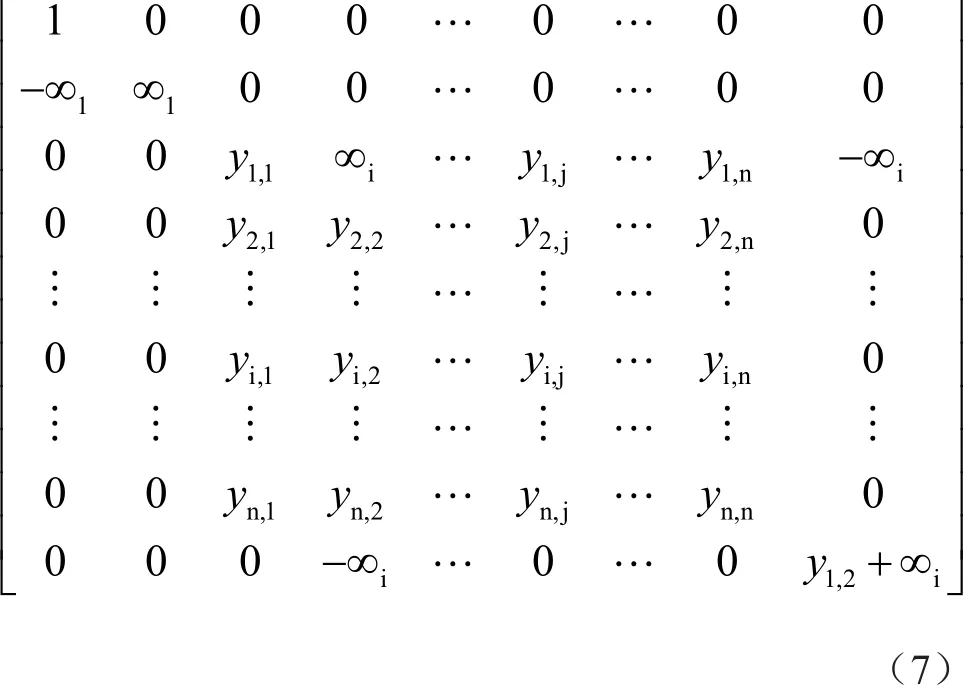
第4步：将由方程式（3）或方程式（4）表示的其余Yi终端的无穷变量对添加到矩阵（7）的第2列中的合适位置，以实现DDCC+或DDCC-的无穷变量符号。采用此操作将现有的导纳项复制到矩阵（5）的第1列，从而得到所需传递函数的分子。例如，通过将±∞i对添加到矩阵（7）的第2列，可将y1,2项复制到矩阵（5）的第1列中。然后得到所需的分子，如矩阵（8）所示。将无穷变量对添加到第2列，相当于将输入电压信号施加到节点2处所增加的Yi终端，得到的矩阵表示综合电路的完整矩阵。

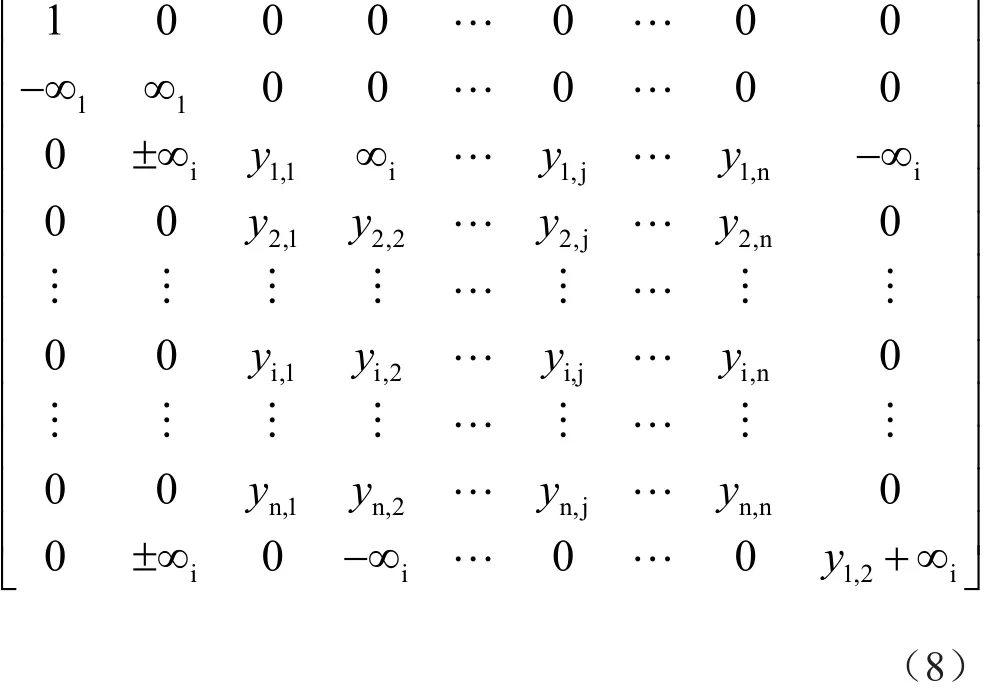
可以看出，在起始矩阵（5）中，节点1被选为输入电压节点，而其他节点为输出节点。在矩阵（6）中，节点1和节点2通过零子或同等物连接到输入节点，而其他节点为输出节点。第4步中，将无穷变量对添加到第3步中所得矩阵的第2列，相当于将输入电压信号注入到DDCC的一个Y终端。因此，可对具有高阻抗和多输入多输出特性的电路进行综合。

2 应用实例

利用最小数量的具有Q品质因素和极点频率正交调整参数的无源元件来综合双二阶电压模式通用滤波器。传递函数的分母选为：

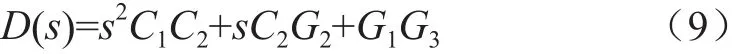
方程式（9）由矩阵（10）按照第1步的程序以矩阵（1）的形式表示：

在第2步中，可通过矩阵（10）得到等效NAM（11）和矩阵（12）。在矩阵（11）中，节点1选为输入节点，节点2和3选为输出节点，分别用Vout1和Vout2表示。在矩阵（12）中，将输出电压节点Vout1和Vout2分别移动到节点3和4。

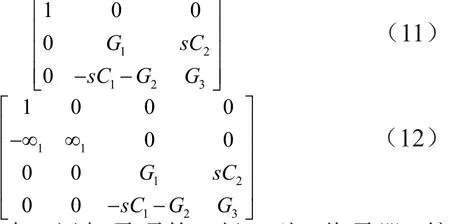
应用第3步，添加零项的3行3列，将零器-镜元件对（由∞2、∞3和∞4表示）引入到矩阵（12）的右侧和底部。因此，矩阵（12）可扩展为矩阵（13），共有8个扩展矩阵（12）的替代选择，分别如图4～图11所示，对应的矩阵分别为式（14）～式（21）所示。

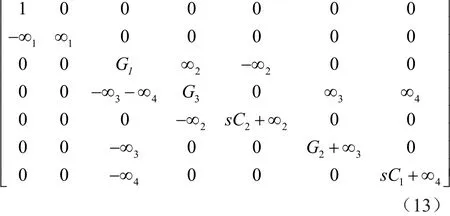
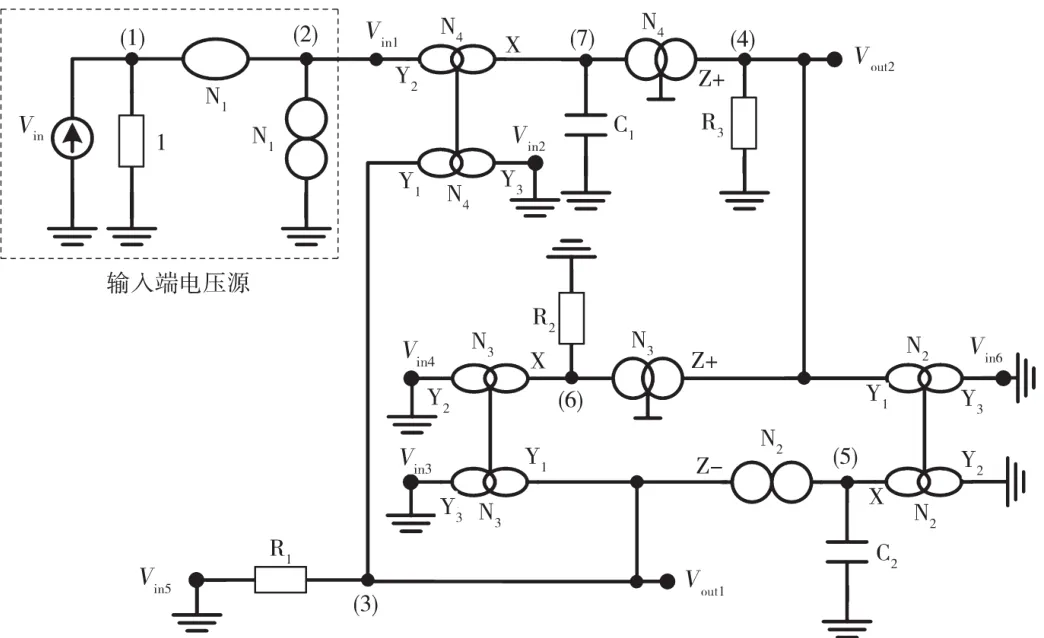
图4 基于DDCC滤波器的奇异结构表示（选择1）（矩阵14）

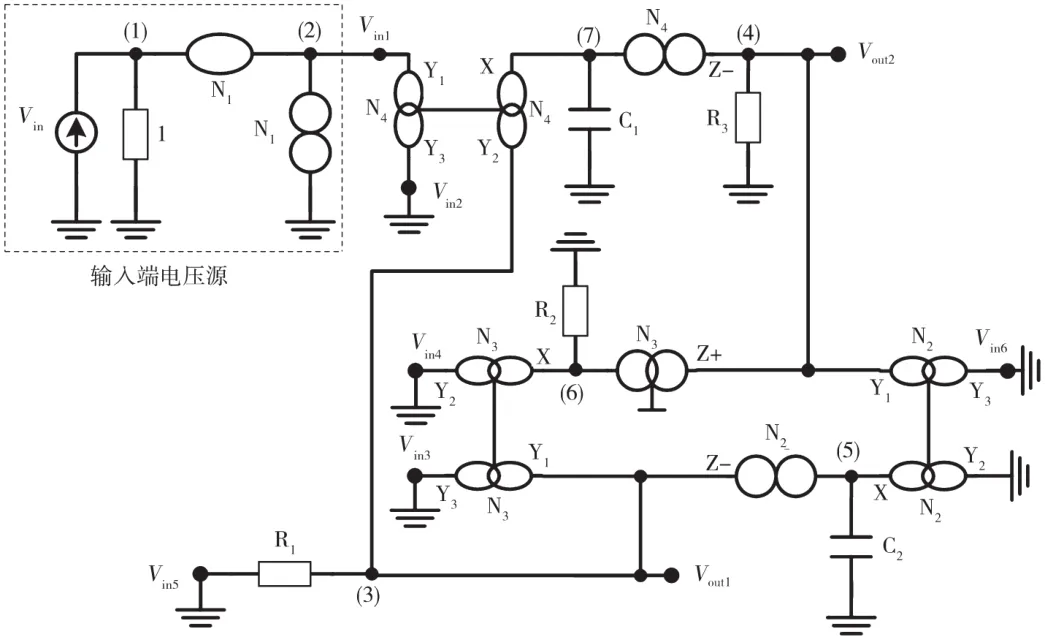
图5 基于DDCC滤波器的奇异结构表示（选择2）（矩阵15）

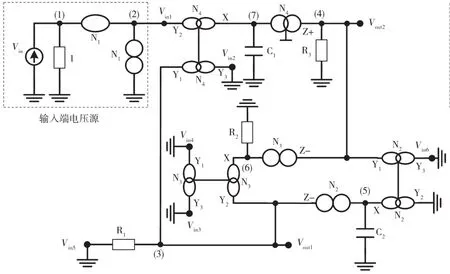
图6 基于DDCC滤波器的奇异结构表示（选择3）（矩阵16）

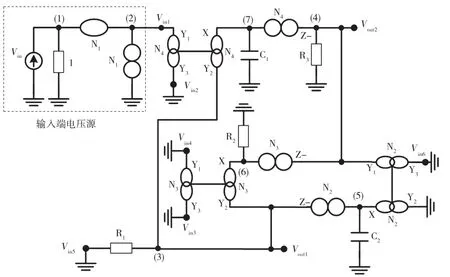
图7 基于DDCC滤波器的奇异结构表示（选择4）（矩阵17）

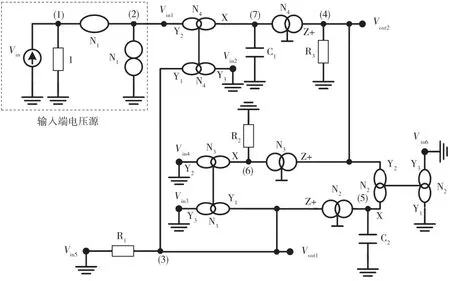
图8 基于DDCC滤波器的奇异结构表示（选择5）（矩阵18）

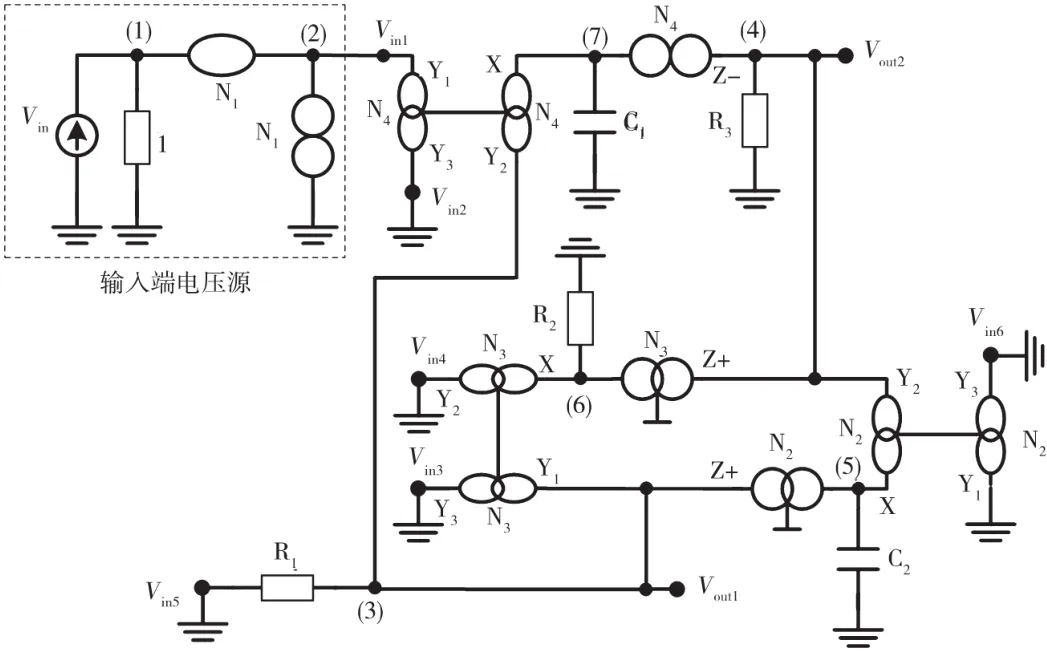
图9 基于DDCC滤波器的奇异结构表示（选择6）（矩阵19）

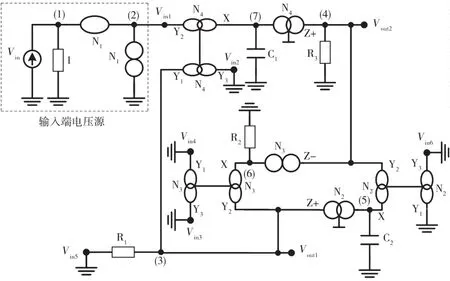
图10 基于DDCC滤波器的奇异结构表示（选择7）（矩阵20）

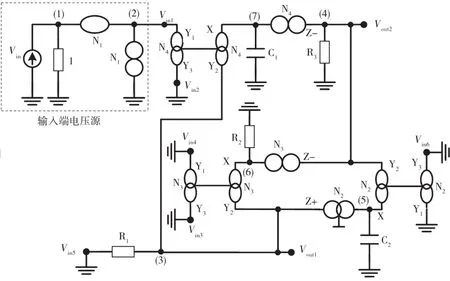
图11 基于DDCC滤波器的奇异结构表示（选择8）（矩阵21）

在矩阵（13）中，DDCC(N2)、DDCC(N3)和DDCC(N4)分别由项±∞2、±∞3和±∞4表示。基于矩阵（3）和矩阵（4）中的NAM符号以及分配给DDCC的终端X的主对角线上的公共节点，DDCC-(N2)的终端X可为节点5，终端Y1连接到节点4，终端Z(DDCC-)连接到节点3。对于DDCC+(N3)，终端X连接到节点6，终端Y1连接到节点3，终端Z(DDCC+)连接到节点4。对于DDCC+(N4)，终端X连接到节点7，终端Y1连接到节点3，终端Z(DDCC+)连接到节点4。DDCC-(N2)的 终 端 Y3，DDCC+(N3)的 终 端 Y3和 端 子 Y2，DDCC+(N4)的终端Y3和终端Y2可用于注入输入电压源。

应用第4步，通过将输入电压源注入到DDCC+(N4)的终端Y2(Vin1)，可将项sC1添加到矩阵（11）的位置(3,1)，可在Vout1是一个高通函数，在Vout2是一个带通函数。该操作相当于将项∞4插入到矩阵（13）的第2列，如矩阵（22）所示。得到的由矩阵（22）表示的滤波器如图4～图11所示，其中Vin2、Vin3、Vin4、Vin5和 Vin6接地。

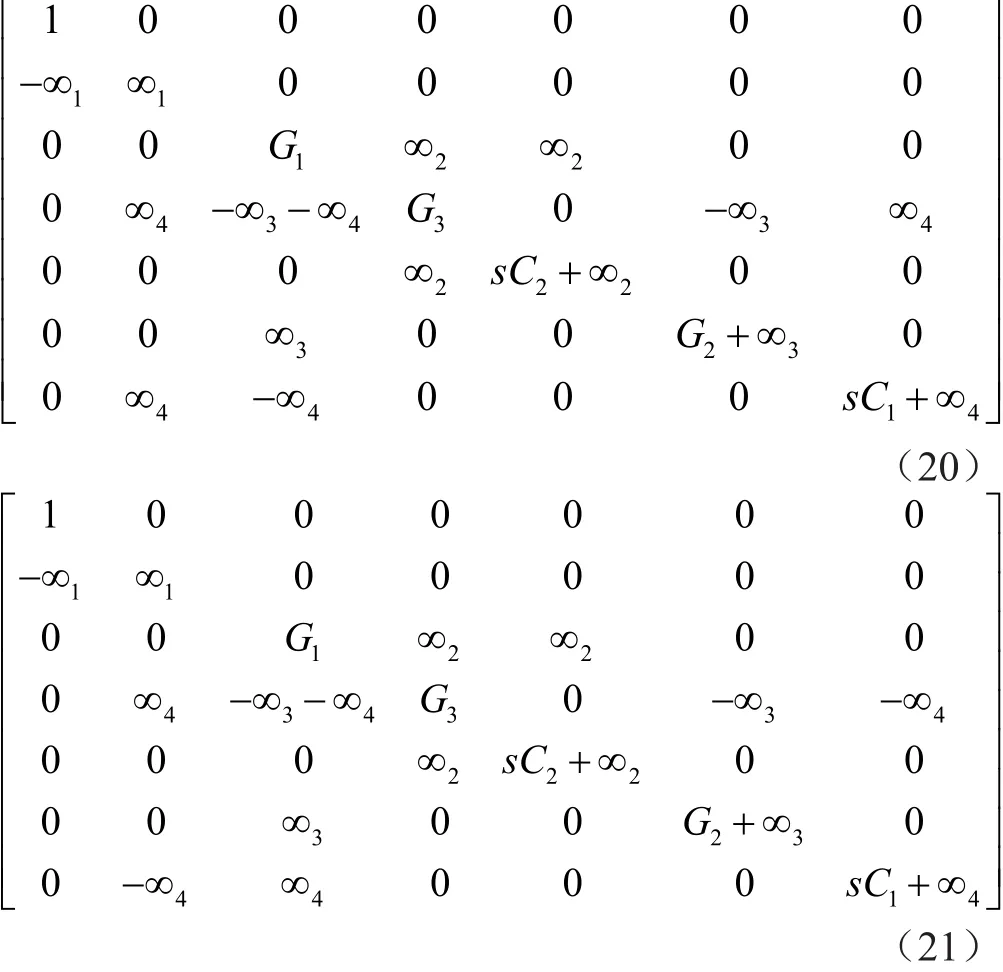
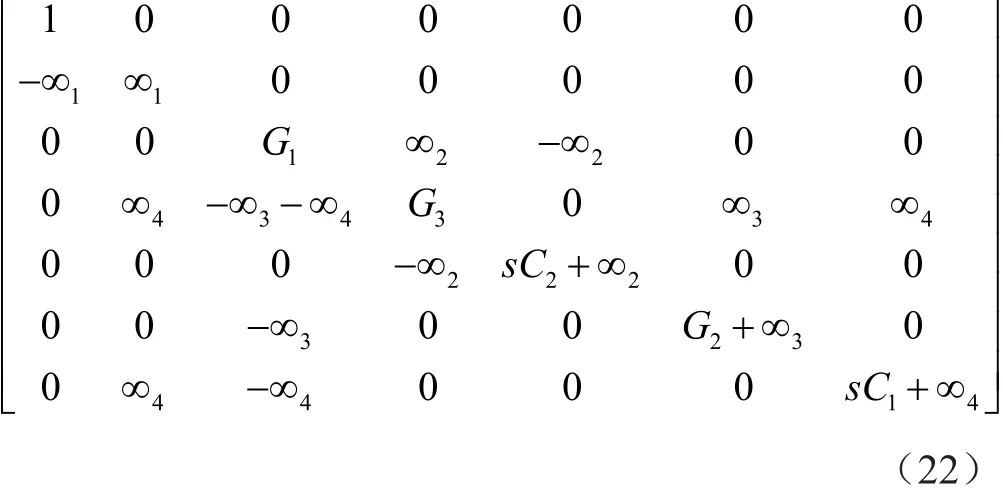
应用第4步，通过将输入电压源注入到DDCC+(N4)的终端Y3(Vin2)，可将项-sC1添加到矩阵（11）的位置(3,1)。导纳矩阵如矩阵（23）所示，在节点Vout1和Vout2得到的传递函数与矩阵（14）中得到的传递函数相同，但是符号相反。其中，接地节点Vin1、Vin3、Vin4、Vin5和Vin6，得到的电路是将输入电压源加到图4中的节点Vin2处，且节点Vin1、Vin3、Vin4、Vin5、Vin6接地。

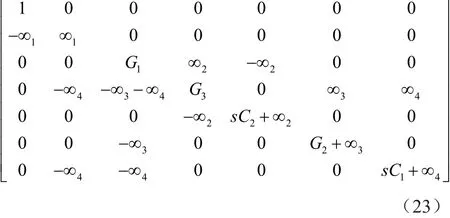
同样，通过将输入电压源注入到DDCC+(N3)的终端Y2(Vin4)，可将项G2添加到矩阵（11）的位置(3,1)，可在Vout1是一个带通函数，在Vout2是一个低通函数。该操作相当于将项∞3插入到矩阵（13）的第2列，如矩阵（24）所示。得到的由矩阵（24）表示的滤波器是将输入电压源加到图4中的节点Vin4处，其中 Vin1、Vin2、Vin3、Vin5和 Vin6接地。

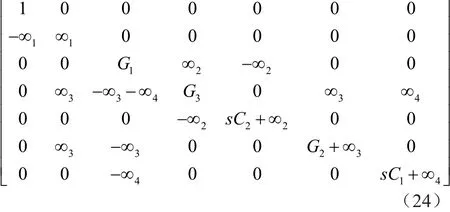
通过将输入电压源注入到DDCC+(N3)的终端Y3(Vin3)，可将项-G2添加到矩阵（11）的位置(3,1)。导纳矩阵如矩阵（25）所示，在节点Vout1和Vout2得到的传递函数与矩阵（24）中得到的传递函数相同，但是符号相反。其中，接地节点Vin1、Vin2、Vin4、Vin5和Vin6，得到的电路是将输入电压源加到图4中的节点Vin3处。

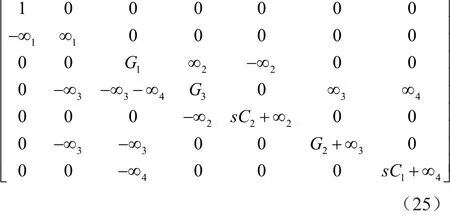
同样，通过将输入电压源注入到R1（Vin5），可将项-G1添加到矩阵（11）的位置(2,1)，可在Vout1是一个低通函数，在Vout2是一个低通函数。该操作相当于将项±G1插入到矩阵（13）的第2列，如矩阵（26）所示。得到的由矩阵（26）表示的滤波器是将输入电压源加到图4中显示节点Vin5处，其中Vin1、Vin2、Vin3、Vin4和 Vin6接地。

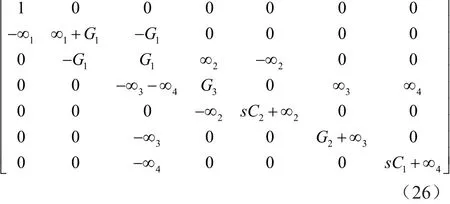
通过将输入电压源注入到DDCC-(N2)的终端Y3(Vin6)，可将项-sC2添加到矩阵（11）的位置(2,1)，可在Vout1是一个带通函数，在Vout2是一个高通函数。该操作相当于将项±∞2插入到矩阵（13）的第2列，如矩阵（27）所示。得到的由矩阵（27）表示的滤波器是将输入电压源加到图4中节点Vin6处，其中Vin1、Vin2、Vin3、Vin4和 Vin5接地。

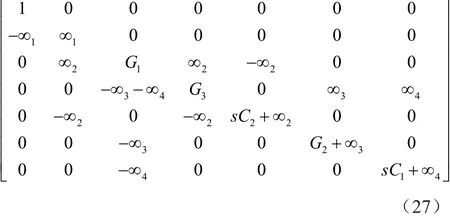
此外，通过将输入电压源注入到DDCC+(N4)的终端Y2(Vin1)和R1(Vin5)，可将项sC1和-G1添加到矩阵（11）的位置(3,1)和(2,1)，可在Vout1是一个陷波函数，在Vout2是一个低通函数。该操作相当于将项∞4和±G1插入到矩阵（13）的第2列，如矩阵（28）所示。得到的由矩阵（28）表示的滤波器是将输入电压源加到图4中节点Vin1和Vin5处，其中Vin2、Vin3、Vin4和Vin6接地。

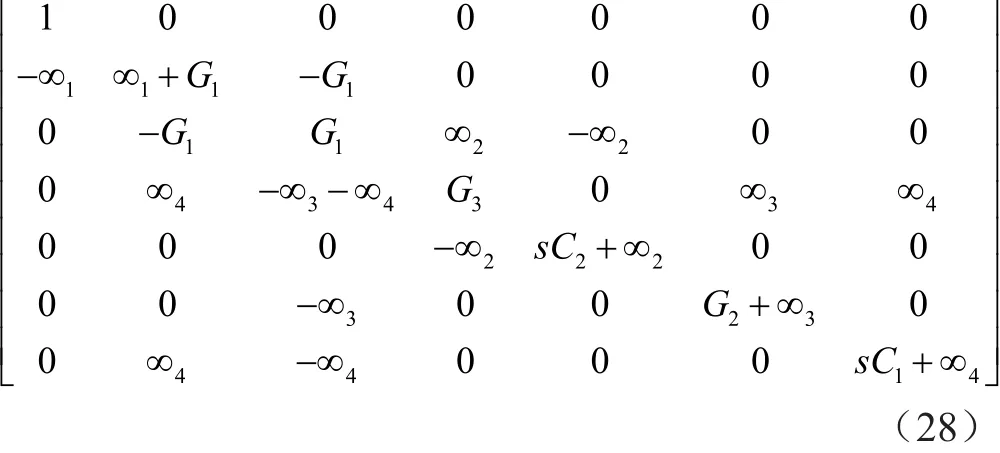
通过同样的方式，可将综合的程序应用于矩阵（14）～矩阵（21）（扩展基于DDCC滤波器的NAM的8种选择）中的选择矩阵（15）～矩阵（21）。导出滤波器的8个等效电路如图4～图11所示。

所提出的电路如图12～图19（基于DDCC滤波器的实际组态）所示，使用3种DDCC、2个接地电容、3个接地电阻。通过使用标准符号，DDCC的端口关系可以用IY1=IY2=IY3=0，VX=VY1-VY2+VY3和IZ=±Ix来表示[23]，其中加号和减号表示传输器是否配置为反相电路或非反相电路，称为DDCC-或DDCC+。通过应用电流副本，很容易得到DDCC的双电流输出。所提出的电路的方程式由每个节点方程式导出，图12～图19对应的是矩阵14～矩阵21和输入电压源未加到输入节点的情形。

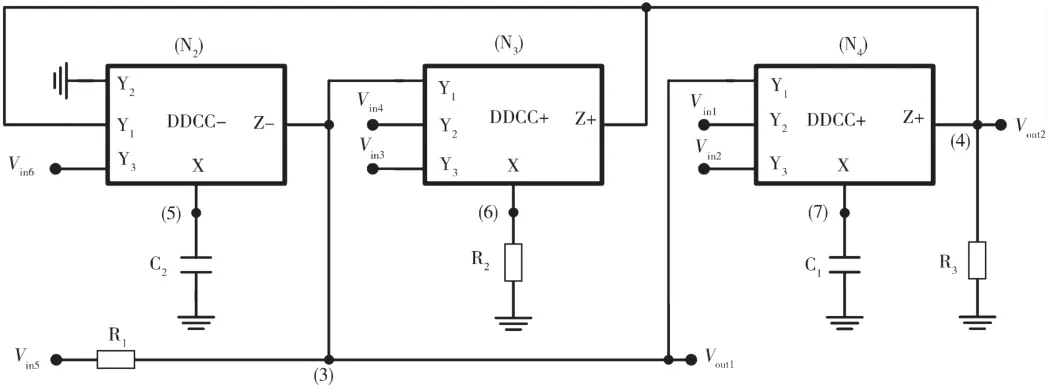
图12 基于DDCC滤波器的实际组态（挑选1）（矩阵14）

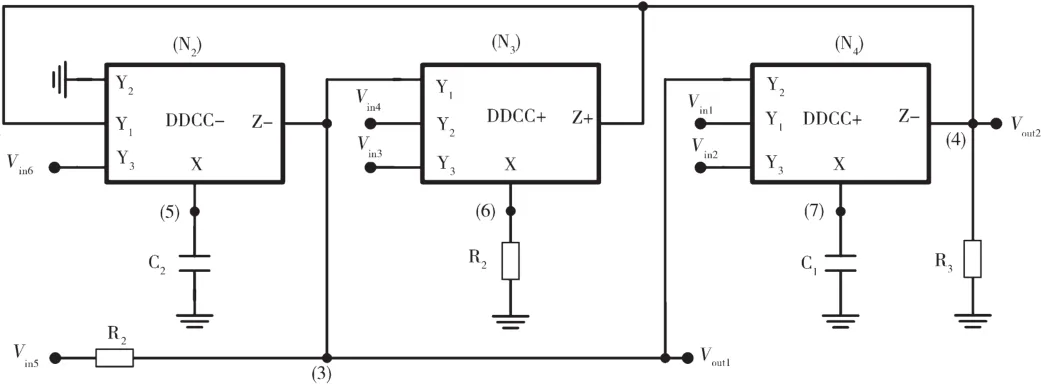
图13 基于DDCC滤波器的实际组态（挑选2）（矩阵15）

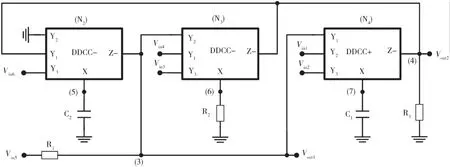
图14 基于DDCC滤波器的实际组态（挑选3）（矩阵16）

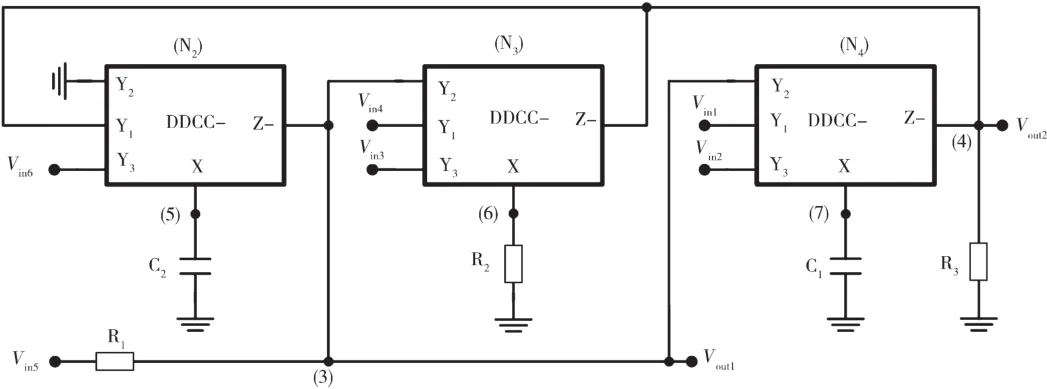
图15 基于DDCC滤波器的实际组态（挑选4）（矩阵17）

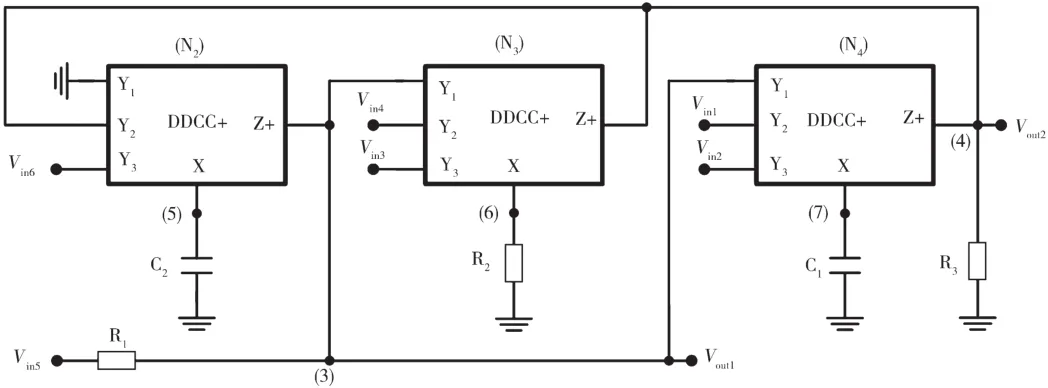
图16 基于DDCC滤波器的实际组态（挑选5）（矩阵18）

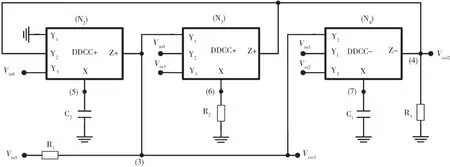
图17 基于DDCC滤波器的实际组态（挑选6）（矩阵19）

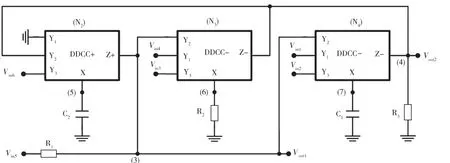
图19 基于DDCC滤波器的实际组态（挑选8）（矩阵21）

方程式（29）和方程式（30）给出了挑选1～挑选8的综合电路的输出传递函数。图12～图19显示了图4～图11中奇异结构等效的实际组态。

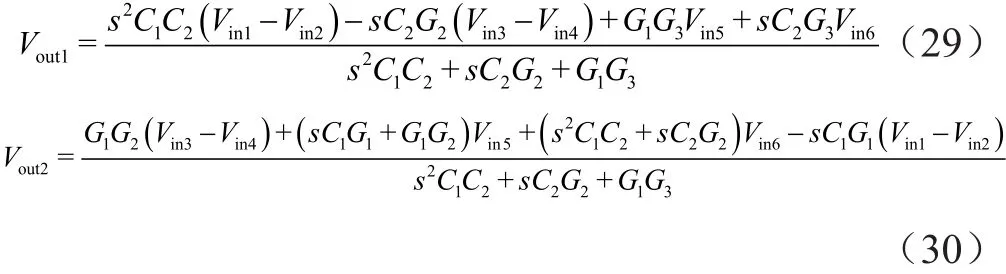
在所有情况下，每个网络的谐振角频率ω0和品质因素Q很容易得到，且可以正交调节。

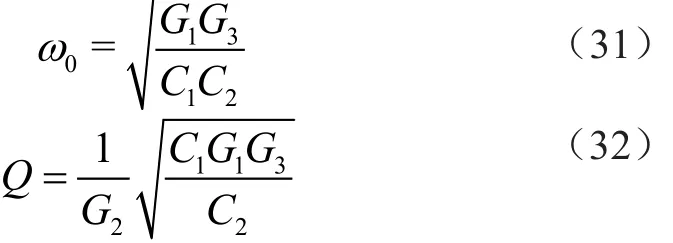
3 得到的基于DDCC的电压模式通用双二阶滤波器的仿真结果

为了验证提出的方法的可操作性，对图12中得到的滤波器[21]使用TSMC 0.35 µm（台湾积体电路制造股份有限公司）过程参数进行电路仿真软件模拟。模拟使用DDCC±的CMOS实现，如图20[24]所示。

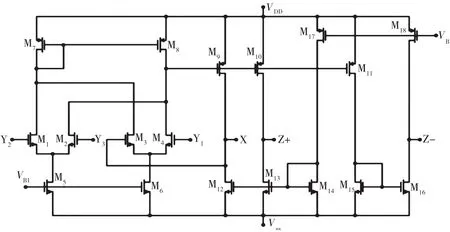
图20 DDCC±的CMOS实现

每个NMOS和PMOS晶体管的长宽比分别为（W/L=5μm/1μm）和（W/L=10μm/1μm）。DDCC±的电源电压是VDD=-VSS=1.65 V，偏压电压是VB1=0.76 V 和 VB2=-0.76 V。 在 Vin1、Vin2、Vin3、Vin4、Vin5和Vin6处用输入电压信号设计图12的模拟频率响应。使用的3个有源元件是DDCC±，无源元件值是R1=R2=R3=10kΩ和C1=C2=15 pF。模拟结果如图21所示。

4 结 论

基于DDCC无穷变量符号和NAM扩展技术，提出了一种对基于DDCC的电压模式通用滤波器进行综合的系统方法，得到的滤波器具有6个输入节点和2个输出节点，只使用接地电容和电阻，即可实现极点频率和品质因数之间的正交控性，且具有低灵敏度。电路仿真软件模拟结果显示了综合电路的可操作性，提出的方法的具有可行性。

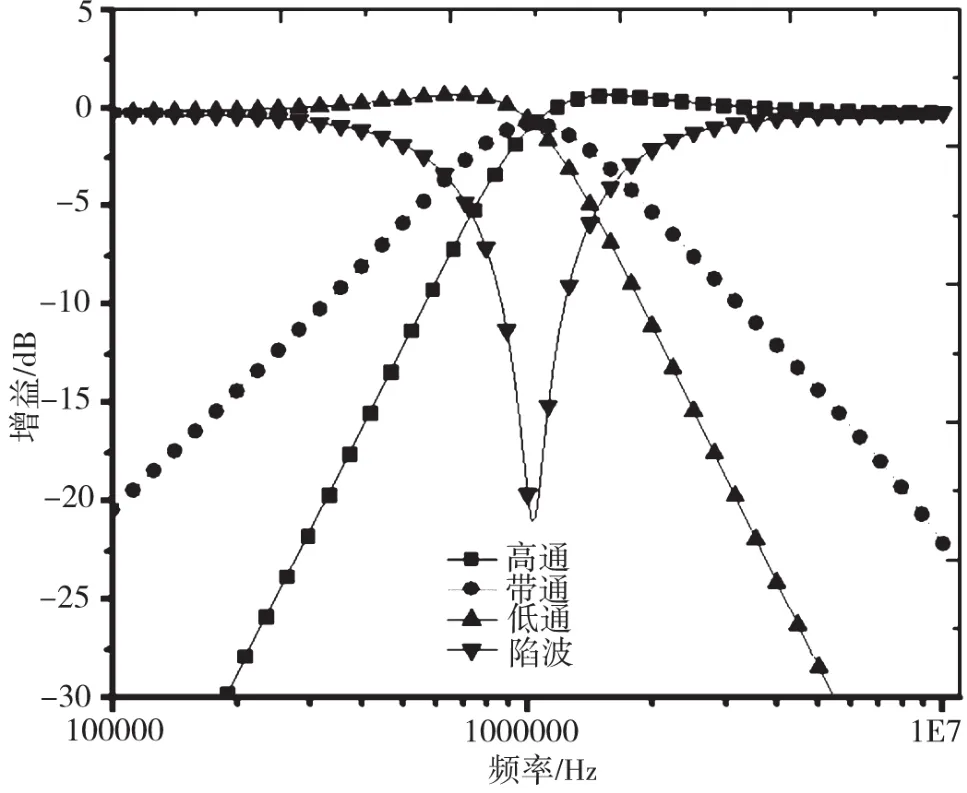
图21 通用电压模式滤波器的频率响应