基于局部敏感直方图的鲁棒目标跟踪

2018-11-17米向荣曹建芳

计算机工程与设计 2018年11期

米向荣，曹建芳

(忻州师范学院计算机科学与技术系，山西忻州 034000)

0 引言

最近提出了大量优秀的跟踪算法[1]，黄清泉等[2]将局部背景信息引入到目标直方图模型中，提高了复杂情况下的跟踪性能；顾鑫等[3]利用局部加权直方图构建目标模型，将目标上下文信息引入到目标直方图模型中，增强了目标外观模型的表观能力；修春波等[4]基于显著性直方图的目标跟踪方法，分别计算目标区域与背景区域的颜色显著性值，弱化背景干扰，提高跟踪鲁棒性；郭金朋等[5]等将SURF特征与Camshift算法进行融合，对目标模板进行实时在线匹配，解决了复杂背景下相似目标干扰问题；Horst

等[6]提出基于颜色直方图的干扰感知跟踪(distractor-aware-tracking，DAT)，通过引入干扰感知模型解决复杂场景下的相似目标混淆问题和跟踪漂移问题，取得了不错的效果。

然而，上述跟踪算法都没能解决剧烈光照变化、情况下的鲁棒目标跟踪问题，本文在DAT算法的基础上提出基于局部敏感直方图的鲁棒目标跟踪。通过局部敏感直方图计算光照不变特征，提高剧烈光照变化情况下的目标外观模型鲁棒性；引入干扰感知模型，将干扰感知模型和颜色概率模型进行加权融合，以此解决复杂背景情况下的目标跟踪漂移问题；通过尺度自适应策略，解决目标尺度估计问题；最后利用公开数据集[7]测试本文算法性能。

1 干扰感知跟踪

文献[6]提出干扰感知跟踪，其在颜色直方图跟踪算法上，引入干扰感知模型，有效降低了复杂情况下的跟踪漂移问题，提高了跟踪鲁棒性。干扰感知跟踪主要分为目标颜色概率模型和干扰感知模型，下面对干扰感知跟踪进行简单介绍：

为了对目标与背景进行区分，利用贝叶斯分类器对目标像素进行建模，则有

(1)

这里P(x∈O|O,BG,bx)表示像素x属于目标的概率，O,BG分别表示目标区域、背景区域，Ω表示区域O和BG的集合，P(x∈O)和P(x∈BG)表示像素x属于区域O和BG区域的概率，P(bx|x∈O)和P(bx|x∈BG)表示区域O和BG中属于区间bx。

(2)

(3)

这里|·|表示计算区域内像素个数。

则式(1)可以简化为

(4)

同时为了提高算法在复杂场景下的抗干扰能力，引入干扰感知模型(即目标-扰动概率模型)，其定义为

(5)

最终目标联合概率模型为

P(x∈O|bx)=βP(x∈O,BG,bx)+
(1-β)P(x∈O,S,bx)

(6)

这里β表示模型融合权重因子，这里设置为0.5。然后，计算目标概率似然响应图有

(7)

这里|W|表示搜索窗口内的像素个数，P(xi,j)表示像素xi,j属于目标的似然概率。似然响应图中最大响应所在位置就是目标所在位置。

2 本文算法

为了解决剧烈光照情况下的跟踪漂移问题，本文提出基于局部敏感直方图的鲁棒目标跟踪，图1为本文算法流程。

图1 本文算法流程

2.1 基于局部敏感直方图的目标跟踪

传统的图像直方图是统计特定灰度值出现的次数，而局部敏感直方图[8](local sensitive histogram，LSH)是对一个像素周围的像素进行统计，计算对应像素点的直方图，然后通过加权形式计算每个点的直方图信息。在计算局部敏感直方图时考虑像素的位置信息，越靠近目标像素中心的像素点权重系数越大

(8)

这里W表示直方图统计像素个数，α是距离惩罚系数，p与q表示像素位置，B表示灰度级数，Q(Iq,b)用于判别q位置处的像素值Iq是否等于像素b，如果Iq=b则Q=1,否则Q=0。

利用局部敏感直方图可以计算光照不变特征(illumination invariant feature，IFF)，其定义为

(9)

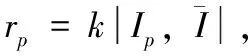
最后通过目标颜色概率模型和干扰感知模型，计算目标联合概率，最后目标似然概率响应图为

(10)

2.2 自适应目标尺度变化

(11)

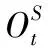
2.3 模型更新

采用线性插值的方法对目标外观模型更新

(12)

为了保证目标尺度估计的鲁棒性，采用线性插值的方法对目标尺度进行更新

(13)

3 实验结果与分析

本文算法的实验平台为VS2013，所有实验均在intel i7-7700k CPU，主频4.2 GHZ，内存32 G的PC上进行。本文算法的参数设置为：模型融合权重因子β设置为0.5，常数k为0.1，权重因子α设置为0.5，目标外观模型学习速率γ为0.1，目标尺度状态学习速率φ为0.2。

利用8组公开数据集测试本文算法在剧烈光照变化、尺度变化和背景嘈杂等情况下的性能，同时与6种算法进行比较：KCF[9]、LSHT[8]、DAT[6]、Struck[10]、TLD[11]和LOT[12]，记录不同算法的整体精确度图和成功率图以及在不同序列上的跟踪误差(又叫中心位置误差)。

中心位置误差(center location error，CLE)：指跟踪目标真实中心坐标与跟踪得到的目标位置之间的欧式距离。

精确度图(precision plot)：表示跟踪目标的CLE小于指定阈值的帧数占跟踪序列帧数的比例。当阈值取为20时，表示算法的精确度得分。

成功率图(success plot)：表示跟踪目标窗口与真实目标窗口之间重叠率大于指定阈值的帧数占总帧数的百分比。一般阈值设置为0.5时，获取算法的成功率得分，但是为了保证算法的鲁棒性，这里用成功率曲线下的面积表示算法的成功率。

测试视频序列属性，见表1。

3.1 算法实验结果

3.1.1 剧烈光照变化情况下特征分析

图2是剧烈光照变化情况下的图像处理结果。在图2(a)中显示弱光和正常情况的图像，图2(b)中是经过局部敏感直方图处理之后的图像，从处理结果中看出局部敏感直方图能最大限度地降低光照变化对图像的影响，说明本文算法利用局部敏感直方图解决光照变化的方法是有效的。

表1 测试视频序列属性

图2 剧烈光照变化情况下的光照不变特征

3.1.2 不同属性视频序列上跟踪结果分析

剧烈光照变化情况下跟踪情况分析：图3为剧烈光照变化情况下7种算法的实际跟踪情况。在剧烈光照变化情况下，目标外观模型发生剧烈变化，此时极易出现跟踪漂移或跟踪失败现象。例如，在图3(b)threllis序列中跟踪人脸从#166到#311帧，人脸受到剧烈光线照射，面部特征发生剧烈变化，此时跟踪器容易发生跟踪失败。从图3(b)第#311帧看出只有本文算法、Struck和KCF算法能较为准确的跟指定目标，而其它算法均出现较大的跟踪漂移，甚至跟踪失败，如LOT算法(因为其主要利用的是灰度特征，对光照变化较为敏感，在剧烈光照变化情况下极易跟踪失败，而本文算法通过利用局部敏感直方图构建光照不变特征，极大降低了光照变化的影响)。同时在man、human8和coke_c等序列中，跟踪目标所受到的主要挑战是剧烈光照变化。通过图3中7种算法实际跟踪情况分析，看出本文算法能很解决剧烈光照变化情况下的跟踪问题。

尺度变化情况下的跟踪情况分析：在图4(a)和图4(b)中目标外观模型(大小)发生尺度变化。在目标跟踪算法中，若目标发生外观模型的变化，容易造成跟踪器跟踪漂移问题，而本文利用自适应尺度分割方法，有效解决了目标尺度变化问题，提高了跟踪精确性。例如在图4(a)dog序列中，从第#1到第#91帧，狗发生尺度变化，因为KCF算法与Struck算法不具备尺度估计策略，所以无法解决尺度变化情况下跟踪漂移问题，降低了跟踪鲁棒性。而在图4(b)中，目标同样发生尺度变化，发现虽然DAT算法具有尺度变化策略，但是DAT算法还是发生跟踪失败，这是因为DAT算法在灰度图像上进行跟踪时，其利用的是单通道的灰度特征，因此效果很差。通过图4(a)和图4(b)看出本文算法能很好地解决目标尺度变化问题。

图3 剧烈光照变化情况下的跟踪情况

图4 目标剧烈尺度变化和背景嘈杂情况下的跟踪情况

背景嘈杂情况下的跟踪情况分析：在图4(c)和图4(d)中跟踪目标处于复杂的背景中，此时受背景干扰极易发生跟踪漂移和跟踪失败。本文算法因为利用干扰感知模型，因此能很好解决背景嘈杂情况下的目标干扰。例如，在图4(c)crossing第#26、#86和#105帧，受背景干扰的影响，LOT、TLD和LSHT算法发生跟踪失败，而本文算法和DAT因为具有干扰感知模型，因此能很好解决背景嘈杂情况下的跟踪漂移问题。

为了更好分析本文算法的优缺点，分别记录本文算法与其它6种算法在测试序列上的整体精确度图和成功率图(图5)。同时，记录此7种算法在不同视频序列上的跟踪误差(图6和图7)。

3.2 算法性能分析

从图5中看出本文算法的精确度得分和成功率得分分别为0.999和0.721，在7种算法中排名第一，说明本文算法能很好的解决目标光照变化、尺度变化和背景嘈杂情况下的精确目标跟踪任务。同时测试本文算法在测试序列上的平均速度为21.2FPS，满足实时性要求。

图6和图7记录7种算法在8个视频序列上的跟踪误差。从coke_c、human8、man和threllis序列上的跟踪误差看出，传统的基于直方图模型的跟踪算法(如DAT、LSHT和LOT)对光照变化较敏感，当跟踪目标受到光照变化的影响，其外观模型发生剧烈变化，此时极易发生跟踪漂移，因此跟踪误差加大。而本文算法通过利用局部敏感直方图和干扰感知模型很好解决了问题。在目标发生尺度变化和背景嘈杂的情况下，本文算法的跟踪误差均小于DAT和LSHT算法，说明本文算法的尺度估计策略和干扰感知模型时有效的。

4 结束语

针对剧烈光照变化、尺度变化和背景嘈杂问题，提出了一种基于局部敏感直方图的鲁棒目标跟踪算法，利用局部敏感直方图构建鲁棒的目标颜色概率模型，降低剧烈光照情况下的跟踪漂移问题，提高跟踪精度；然后引入直方图干扰感知模型，通过加权融合的方式获取目标直方图概率模型，估计目标位置变化；最后通过自适应尺度估计策略解决目标尺度估计问题。实验结果表明，本文算法能很好解决复杂情况下的精确目标跟踪任务，具有一定研究价值。