拉格朗日乘子法求二元函数的最值的惯性误区与正确解析

方 侃

（福州大学至诚学院，福建 福州 350001）

一、二元函数求最值的错解呈现

二元函数z=f（x，y）在定义域上求最值的问题，许多教材都没有给出完整的解决方法，［1］吴传生主编高等教育出版社出版的经济数学—微积分下册有谈到二元函数的最大值与最小值的内容，其中提到：“如果f（x，y）在有界闭区域D上连续，则f（x，y）在此有界闭区域上一定能取到最大值和最小值。而使得函数取到最大值或最小值的点既有可能在此有界闭区域的内部，也可能在此有界闭区域的边界上。如果我们假设，f（x，y）在D上连续，在D内可微且只有有限个驻点，这时候函数f（x，y）在D的内部取得的最大值（最小值）也就是函数的极大值（极小值）。那么，在上述假设下，求函数的最值的过程是：求出函数f（x，y）在D内的所有驻点，然后将对应的函数值与函数在D的边界上的最值进行比较，其中最大（小）的就是最大（小）值。但是这种方法，需要求得函数在D的边界上的最大值和最小值，此过程通常非常复杂。因而在实际问题中，如果函数在D内只有唯一驻点，则该驻点处的函数值就是函数f（x，y）在D上的最大值（最小值）。教材中举的例子也是有唯一驻点的实际例题，用拉格朗日乘子法求出唯一极值点后就是最值点。

二元函数的最值求解是一个难题，笔者在教学中，发现解二元函数最值的一个普遍性错误，以下我们就探讨［2］同济大学数学系主编高等教育出版社出版的《微积分》下册的教材关于有界闭集D上连续可微的二元函数求最值用拉格朗日乘子法计算时的错误解法。

同济大学数学系编的微积分下册P111页谈到：“下面讨论如何求二元函数z=f（x，y）在有界闭区域上的最值问题。假设函数f（x，y）在有界闭区域D上连续而且可微，则由连续函数的最大值最小值定理可知在D上必存在最大值和最小值。如果最大值或最小值在D的内部取得，那么这些最大值点或最小值点必然是驻点。据此可以先求出f（x，y）在D的内部所有驻点的函数值。然后利用求解条件极值的方法求出f（x，y）在D的边界上的最大值和最小值。最后，将上面所得到的这些值加以比较，其中最大的就是最大值，最小的就是最小值。”

例题4；求f（x，y）=2x2+y2在闭区域D={（x，y）|2（x-1）2+（y-1）2≤12}上的最大值和最小值。

解：先用拉格朗日乘子法求出f（x，y）在边界D={（x，y）|2（x-1）2+（y-1）2=12}上可能的极值点。作 L（x，y，l）=2x2+y2+l［2（x-1）2+（y-1）2-12］，求解方程组：

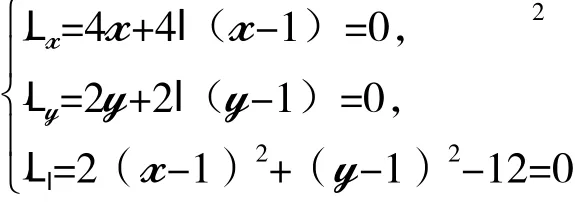
解得f（x，y）在椭圆边界D={（x，y）|2（x-1）2+（y-1）2=12}上的两个可能极值点M1（3，3），M2（-1，-1）。

再求f（x，y）在D内部{（x，y）|2（x-1）2+（y-1）2＜12}的可能极值点，由于fx=4x，fy=2y，因此由fx=fy=0解得唯一驻点M3（0，0）。

由于f（3，3）=27，f（-1，-1）=3，f（0，0）=0，因此f（x，y）在D上的最大值为27，在D上的边界点M1取得；最小值为0，在D的内点M3取得。

现在按照以上解题思路和过程，解答P113页3.（3）：f（x，y）=1+xy-x-y，D是由曲线y=x2和直线y=4所围成的有界闭区域。

解：先用拉格朗日乘子法求出f（x，y）在边界D={（x，y）|y=x2}上可能的极值点。作L（x，y，l）=1+xy-x-y+l（y-x2），求解方程组：

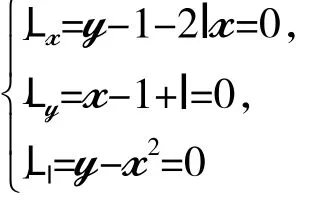
解得f（x，y）在边界上的两个可能极值点M1（1，

先用拉格朗日乘子法求出f（x，y）在边界D={（x，y）|y=4}上可能的极值点。作L（x，y，l）=1+xy-x-y+l（y-4），求解方程组：

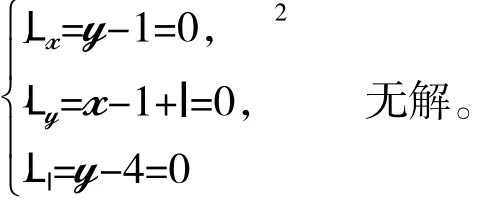
再求f（x，y）在D内部{（x，y）|x2＜y＜4}的可能极值点，由于fx=y-1，fy=x-1，因此由fx=fy=0解得唯一驻点M3（1，1）。

这样算出的答案与习题后的参考答案一致，然而这个答案是错误的。因为f（-2，4）=-9，f（2，4）=3，而这两个点显然包含在D={（x，y）|x2≤y≤4}这个有界闭区域上，因此f（-2，4）=-9，f（2，4）=3，就分别是 f（x，y）=1+xy-x-y在D={（x，y）|x2≤y≤4}这个有界闭区域上的最小值和最大值。

二、二元函数求最值的错因分析

我们从一元函数求最值来分析。一元函数y=f（x）在闭区间［a，b］上求最值的过程：先求极值点，再比较端点y=f（a），y=f（b）的值，最后得到最大最小值。因此，二元函数z=f（x，y）在有界闭区域Dxy求最值，我们同样是要先求二元函数z=f（x，y）在D的内部的极值点，再跟边界值比较，得到最大值最小值。只是二元函数的边界要比一元函数复杂许多，一元函数就是两个端点，二元函数是由若干条曲线构成。在求内部极值点的时候，上面例4的过程没有任何问题，问题出在用拉格朗日乘子法求边界值的时候，其实仍然解决的是内部的极值问题，而不是最值问题，要解决最值，还必须把边界约束条件代入二元函数z=f（x，y）化为一元函数y=f（x）后的x端点值考虑进去比较。

三、二元函数求最值的正确解法

例4解（一）：的第一部分用拉格朗日乘子法求完，必须再跟两个x的端点后的二元函数值比较结果终比较过，虽然答案不变，但那只是因为极值点恰好是最值点，事实上，［3］顾江永李红玲的文章中列出四种解法的解法三，用拉格朗日乘子法求边界点的时候也是忽略了要用端点值来比较的这个细节问题。此外，例四也可以用参数代换法化为一元函数来解题。

例4解（二）：先求f（x，y）在D内部{（x，y）|2（x-1）2+（y-1）2＜12}的可能极值点，由于fx=4，fy=2y，因此由fx=fy=0解得唯一驻点M3（0，0）得f（0，0）=0。

将两个驻点代入函数得f1（q）=27，f2（q）=3。

而［2］教材中课后习题3.（3）答案就错了，正确的解法如下：

法一（拉格朗日乘子法）：

解：内部问题：求f（x，y）在D内部{（x，y）|x2＜y＜4}的可能极值点，由于fx=y-1，fy=x-1因此由fx=fy=0解得唯一驻点M3（1，1）。

边界问题：按照上面第一次解答所述的过程用拉格朗日乘子法求出极值点后，再比较端点值f（-2，4）=-9，f（2，4）=3，由此比较得到f（x）的最小值为-9，最大值为3。

法二（化为一元函数）：

解：内部问题：求f（x，y）在D内部{（x，y）|x2＜y＜4}的可能极值点，由于fx=y-1，fy=x-1因此由fx=fy=0解得唯一驻点M3（1，1）.

边界问题；将y=x2（-2≤x≤2）代入f（x，y）得，f（x）=1+x3-x-x2，f ′（x）=3x2-1-2x=0，得驻加上端点x=±2。

将y=4（-2≤x≤2）代入f（x，y）得，f（x）=1+4x-x-4=3x-3，由此比较得到f（x）的最小值为-9，最大值为3。

四、二元函数求最值的总结启示

在闭区域上连续可微的二元函数的最值问题，用拉格朗日乘子法求以边界曲线为约束的条件极值，得到的仅仅是极值，和将边界曲线代入二元函数化为一元函数求导得到的极值点性质是一样的，都只能解决的是极值。要想得到最值，必须把边界曲线代入二元函数化为一元函数后，一元变量的端点值考虑进去，最后比较得到的才是最大值和最小值。文章纠正了［2］《微积分》下册第六章关于用拉格朗日乘子法求在有界闭区域上连续可微的函数的最值过程中的一个惯性思维解题的错误。二元函数求最值的题型通常是困难的，解决此类问题，必须要细心，注重培养思维的严谨性。平常教学中，我们应尽量降低难度，重点立足于解决最值的应用问题,即唯一驻点就是最值点的实际问题，以便学生能更好理解此类解法的本质。