例谈不等式在高考解题中的应用

☉山东省肥城市第一高级中学 楚岚天

利用导数证明不等式是每年高考中函数与导数压轴题比较常见的考查方式，往往通过将不等式转化为相关的函数最值来证明不等式，其主要解题思想是依据函数在固定区间的单调性，通过求导直接求得函数的最值（最大值或最小值），然后由f（x）≤f（x）max或f（x）≥f（x）min的转化来直接证得不等式.而由于证明不等式时所转化的函数形式各样，切入点较多，证明的方法也各不一样.

一、真题在线

例题（2018·全国卷Ⅰ文·21）已知函数f（x）=aexlnx-1.

（1）设x=2是f（x）的极值点，求a，并求f（x）的单调区间；

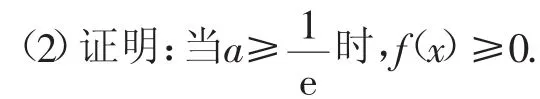
分析：（1）通过求导得到f′（x），由f′（2）=0即可确定参数a的值；再由f′（x）的正负取值来确定f（x）的单调区间.（2）结合条件所要证明的不等式，即转化为证明f（x）的最小值f（x）min≥0.

二、思维方法

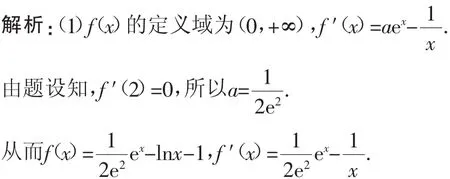
当0＜x＜2时，f′（x）＜0；当x＞2时，f′（x）＞0.

所以f（x）在（0，2）上单调递减，在（2，+∞）上单调递增.

（2）证法1：官方标准答案——构造函数法.

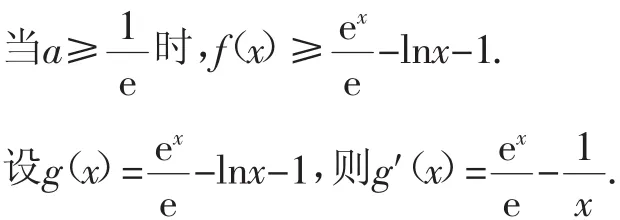
当0＜x＜1时，g′（x）＜0；当x＞1时，g′（x）＞0.

所以x=1是g（x）的最小值点.

故当x＞0时，g（x）≥g（1）=0.

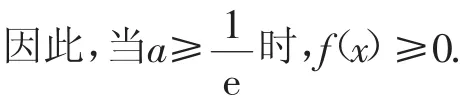
证法2：构造函数法.

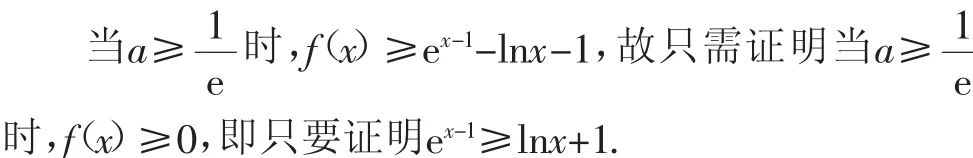
设g（x）=ex-1-x，则g′（x）=ex-1-1.

当0＜x＜1时，g′（x）＜0，g（x）单调递减；

当x＞1时，g′（x）＞0，g（x）单调递增.

所以x=1是g（x）的最小值点，故当x＞0时，g（x）≥g（1）=0.所以ex-1≥x，当且仅当x=1时等号成立.

以上不等式两边取对数可得x-1≥lnx，当且仅当x=1时，等号成立.

从而x≥lnx+1，当且仅当x=1时等号成立.

所以ex-1≥x≥lnx+1.

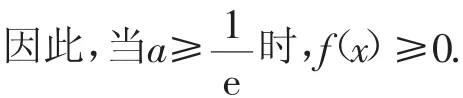
证法3：构造两个函数.

当0＜x＜1时，g′（x）＜0，g（x）单调递减；

当x＞1时，g′（x）＞0，g（x）单调递增.

所以x=1是g（x）的最小值点，最小值为g（1）=ae≥1.

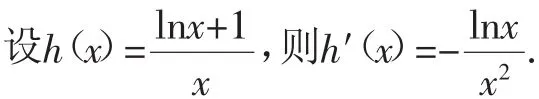
当0＜x＜1时，h′（x）＞0，h（x）单调递增；

当x＞1时，h′（x）＜0，h（x）单调递减.

所以x=1是h（x）的最大值点，最大值为h（1）=1.

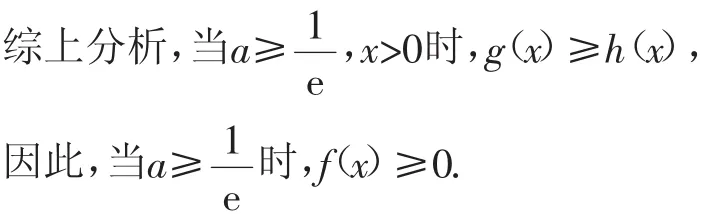
证法4：分离参数法.

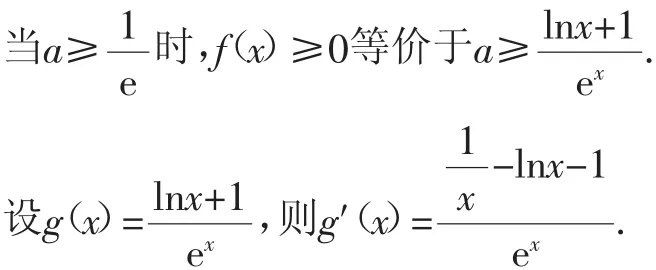
当x＞0时，h′（x）＜0，h（x）单调递减.

因为h（1）=0，所以当0＜x＜1时，h（x）＞0，从而g′（x）＞0，g（x）单调递增；当x＞1时，h（x）＜0，从而g′（x）＜0，g（x）单调递减.

证法5：分析法.

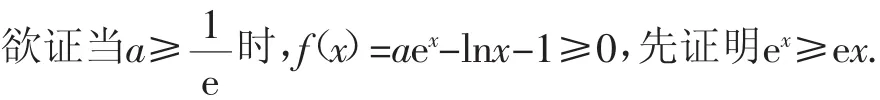
设g（x）=ex-ex，则g′（x）=ex-e.

当0＜x＜1时，g′（x）＜0，g（x）单调递减；

当x＞1时，g′（x）＞0，g（x）单调递增.

所以x=1是g（x）的最小值点，最小值为g（1）=0，所以ex≥ex成立.

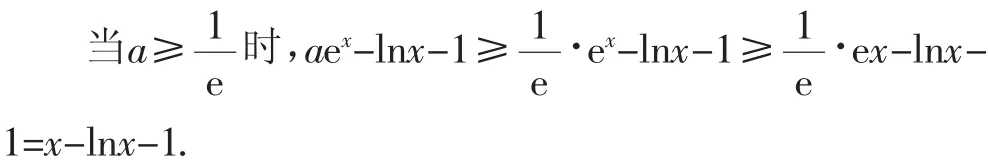
故欲证明aex-lnx-1≥0，只需证明x-lnx-1≥0.

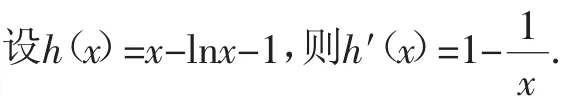
当0＜x＜1时，h′（x）＜0，h（x）单调递减；

当x＞1时，h′（x）＞0，h（x）单调递增.

所以x=1是h（x）的最小值点，最小值为h（1）=0.

所以x-lnx-1≥0成立.

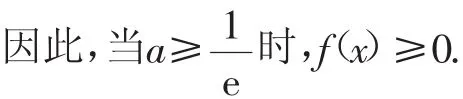
三、技巧总结

（1）利用导数证明不等式成立问题的常用方法概括起来主要有以下几种：

①直接将所要证明的不等式转化成某个函数的最值问题.

若证明f（x）＜g（x），x∈（a，b），可以构造函数F（x）=f（x）-g（x），如果F′（x）＜0，则F（x）在（a，b）上是减函数，同时若F（a）≤0，由减函数的定义可知，x∈（a，b）时，有F（x）＜0，即证明了f（x）＜g（x）.

②将待证不等式转化为两个函数的最值进行比较来证明.

在证明不等式中，若待证不等式无法转化为一个函数的最值问题，此时往往可借助两个函数的最值来证明，例如，要证明f（x）≥g（x）在D上成立，只需证明f（x）min≥g（x）max即可.

③若所证函数不等式通过移项后构成新函数的最值易求，可直接通过移项构造函数证明.

（2）构造函数法证明不等式的基本步骤如下：

①作辅助函数h（x），一般取不等号两端的函数之差或之商为辅助函数；

②对h（x）求导，并确定h′（x）在区间上的符号；

③判断h（x）的单调性；

④求出h（x）在所给区间上的极值；

⑤根据函数单调性或极值的符号证明所需证明的不等式.

若所证不等式两边关于某一变量的关系式的构成比较复杂，直接构造函数后不易求导数或所求导数式不易研究函数性质，可先换元后再求解.H