高考中椭圆试题的解法探源
2018-11-17山东省肥城市第一高级中学刘子昂
☉山东省肥城市第一高级中学 刘子昂
纵观近年高考数学试卷中的选择题和填空题,圆锥曲线中涉及椭圆的题目出现的频率非常高,亮点也颇多.要处理好此类问题,除了熟练掌握椭圆的定义、方程与几何性质外,还要结合题目中的已知条件,准确巧妙用好题中对应的特殊点,从而避免少走弯路,达到快速、有效、准确解题的目的.
一、求线段的长度
例1 已知O为坐标原点,设F1,F2分别是椭圆的左右焦点,P为椭圆C上任意一点,自点F1作∠F1PF2的外角的平分线的垂线,垂足为H,则|OH|=( ).
A.a B.b C.2a D.2b
分析:常规方法是确定点P的位置,连接PF1,PF2,延长F1H交PF2的反向延长线于点Q,结合角平分线的性质以及椭圆的定义得到|QF2|=2a,再结合中位线定理即可得到|OH|的值,利用椭圆的定义来处理,要求必须数形结合,并借助平面几何的相关知识来处理,技巧性要求高.而通过特殊点的选取,淡化椭圆的相关定义与几何性质,简化运算,可以更为有效快捷地处理与解决问题.
解:由于点P为椭圆C上任意一点,取其特殊点P位于椭圆C的左顶点处,此时P,F1,F2三点都在x轴上,那么∠F1PF2为零角,则自点F1作∠F1PF2的外角的平分线的垂线,垂足为H,此时垂线为x=-a,P,H重合,可得|OH|=a.故选A.
点评:对应变化不定的点的位置问题,同时涉及相关角的外角的角平分线以及垂线问题,处理起来要数形结合,而通过特殊点的选取,处理起来更为直观快捷,从而省去对椭圆定义的巧妙转化与应用,以及平面几何中相关知识的综合与应用,使得一般问题特殊化,操作起来更为特殊,且不失一般性,求解更加快捷易求.
二、离心率的确定
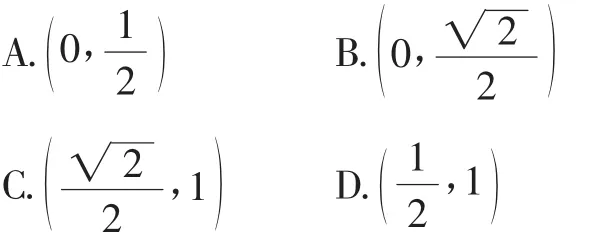
分析:常规方法是设出点P的坐标,根据平面向量的坐标运算并结合PF—→1·PF—→2<0建立不等式,再通过点P的坐标所满足的条件加以代换,结合椭圆的离心率公式以及隐含条件来确定离心率的取值范围问题,处理起来计算量比较大.而通过取特殊点P位于椭圆C的上顶点处,假定此时∠F1PF2为直角,求解此时椭圆的离心率,并结合钝角的性质以及离心率的隐含条件来确定椭圆C的离心离的取值范围,数形结合直观,求解转化巧妙.

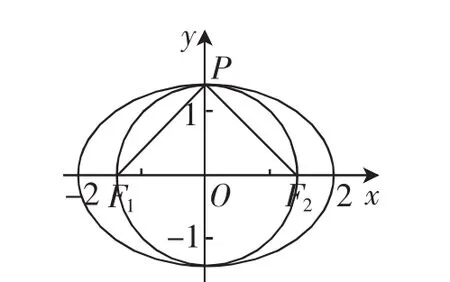
图1
点评:对于无法确定的点的存在性问题,巧妙借助以F1F2为直径的圆与椭圆的关系来确定∠F1PF2的情况,利用∠F1PF2为直角时椭圆离心率的取值,并加以数形结合直观来分析满足条件时椭圆的离心率的取值情况.这样处理问题可以更有效地简化计算,同时数形结合更为直观,省去繁杂的推理与运算过程,提高效益.
三、关系式的转化
分析:常规方法是设出∠IF1F2=α与∠IF2F1=β,得到kIF·
1kIF2=-tanαtanβ,延长F1P到点Q,且|PQ|=|PF2|,通过边角之间的关系转化.在△QF1F2中,结合正弦定理得到对应的关系式,并利用两角和与差的余弦公式来处理,涉及的知识点比较多,计算也比较繁杂.而通过特殊点的选取,使得点P位于双曲线C的上顶点处,方便确定△PF1F2的内切圆I的位置,设出圆的半径,可以简单快捷地在直角三角形中确定对应边之间的关系,结合勾股定理即可确定r的关系式,同时对应直线的斜率也比较方便处理与转化.
解:由于点P是椭圆C上的一个动点,取其特殊点P位于椭圆C的上顶点处,如图2.
设△PF1F2的内切圆I的半径为r,结合内切圆的性质并利用勾股定理可得(a-c)2+r2=(b-r)2,整理有

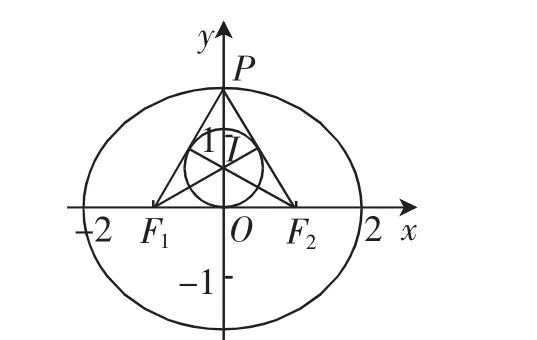
图2
点评:对应变化不定的点的位置问题,通过特殊点的选取,使得对应三角形的内切圆位置的确定、直线的斜率的求解等变得更为方便易求,处理起来更为直观快捷,从而省去对椭圆定义、平面几何、三角函数等综合知识的熟练掌握与应用,使一般问题特殊化,运算起来更为快捷方便,而且不失一般性.
四、几何图形的处理
分析:常规方法是设出点P的坐标,进而确定直线PA的方程,求解点M的纵坐标,从而计算|BM|的值.同理计算|AN|的值,再结合四边形ABNM的面积公式加以转化与化简,进而确定对应的面积.而通过特殊点的选取,利用点P的极端情况,巧妙转化四边形ABNM为极端三角形问题,进而结合三角形的面积公式来求解,通过极端思维处理,更为快捷简单.
解:设A1(-2,0),B1(0,-1).
当P→A1时,此时四边形ABNM→△AA1B,此时S△AA1B=
当P→B1时,此时四边形ABNM→△ABB1,此时S△ABB1=
而P为第三象限内一点且在椭圆C上,根据“两边夹”原理知,四边形ABNM的面积为2.
点评:对于变化不定的四边形问题,通过特殊点的选取,结合极端思维,使得平面图形简单化,借助“两边夹”原理,从而求解起来更为直观简单,处理方式更为巧妙,简化运算,提升效率.涉及平面几何图形的求解问题,经常采取此特殊法处理,寻找特殊的线段、三角形、四边形等特殊图形来分析与处理,从而使得问题解决起来更直观有效.
其实,圆锥曲线中的基本概念、基本方程、基本公式等都是高考中常考的重要知识点之一,对于考查的选择题和填空题,有时题目比较容易,有时题目比较难,都不要轻视,要巧妙通过动手、动脑,融会贯通,化一般为特殊来巧妙处理,真正达到“动后熟悉,熟后思考,思后悟理,悟后掌握”的解题效果,全面培养数学素养,提升数学能力.H
