多维剖析,夯实基础,提升数学核心素养*
——以函数零点的问题为例
2018-11-17安徽省太和县太和中学
☉安徽省太和县太和中学 岳 峻
一、核心素养的培育
《普通高中数学课程标准》(2017年版)强调:“数学教育的本质是提升学生的数学素养,引导学生会用数学眼光观察世界,会用数学思维思考世界,会用数学语言表达世界.”这就要求通过高中数学课程的学习,学生能获得进一步学习,以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验(简称“四基”);提高从数学角度发现和提出问题的能力、分析和解决问题的能力(简称“四能”).在学习数学和应用数学的过程中学生能发展数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析等数学学科核心素养[1].
数学教学中,数学学科核心素养的落实的迫切性日趋引起重视.
数学概念是抽象的,抽象的东西只能获得具体事例的支持,通过思维的深层抽象来实现思维的浅层,再现创造思维的完整性和特异性,并透彻地理解新的概念.倘若没有具体实例来阐释,就无法理解清楚新概念.同样地,课程标准制定专家们在提出新理念的同时给出相应的浅显易懂的教学实例,这样才有利于新理念的领会和落实[2].
在学校教育中,提升数学核心素养的主阵地就是课堂教学,而教学的载体是数学学科知识的学习、内化.为发展学生的核心素养而教,需要“仰望星空、脚踏实地”的行动.作为数学教育的一线教师,结合平时的教学内容如何引领学生剖析已知信息、学会审题、横延纵拓,如何提高学生分析和解决问题的能力,如何提升学生的数学核心素养,这是摆在我们一线数学教师面前的现实问题[3].
二、例析核心素养的培育
函数零点的问题往往以函数为“生”,方程为“旦”,导数为“净”,性质为“丑”,将函数、导数、方程、不等式的应用这台压轴大戏“表演”得绘声绘色,以发展学生数学学科核心素养为导向,创设合适的问题情境,诱导学生思考,引导学生把握数学内容、知识和技能的本质,与数学学科核心素养的达成有机结合.因此,涉及函数零点的问题越来越受到高考命题者的青睐.
为此,在函数零点的问题的教学过程中,笔者结合具体案例,引导学生剖析试题的条件和结论这两个信息源,力求从语法结构、逻辑关系、数字含义、结构特征、知识储备等各方面真正弄懂题意,提取有效信息,挖掘隐含信息,提炼关键信息,引导学生“悟”出解决问题的途径,让其“现出原形”.在教学实践的基础之上,本文对其实践过程中可操作性的层面加以提炼,剖析其内在的数学核心素养,循循善诱地“诱导”学生用数学眼光观察世界,用数学思维思考世界,用数学语言表达世界.权作笔者对数学核心素养的落实作一些尝试,以供同仁探讨[4].
典例 (2018届安徽省太和中学冲刺卷)已知函数f(x)=ax+lnx+1.
(1)当a=-1时,证明:lnx≤x-1;
(2)讨论函数f(x)零点的个数.
素养分析1:本题函数是建立在基本初等函数y=lnx的基础之上的超越函数,而函数y=lnx的一个重要特征就是过定点(1,0),自然想到f(1)=a+1.当a=-1时,f(x)=lnx-x+1,f(1)=0,要证明lnx≤x-1,即f(x)≤0,只需证f(x)max=f(1)即可.为此势必应用导数的正负研究函数f(x)的单调性,进而求解其最大值.借此帮助学生掌握必需的数学知识、技能、思想和方法,有逻辑地表达与交流.
解析:(1)当a=-1时,f(x)=lnx-x+1,定义域为(0,
令f′(x)>0,则0<x<1;令f′(x)<0,则x>1.
所以函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,所以f(x)≤f(1)=0.
所以lnx≤x-1.
素养分析2:函数f(x)零点的个数势必应用导数的正负研究函数的单调性,利用零点存在性定理进行探索,其本质就是考查直观想象、逻辑推理等核心素养,引导学生会用数学眼光观察世界,会用数学思维思考世界,促进学生思维能力、实践能力和创新意识的发展.
(2)方法1:函数f(x)的定义域为(0,+∞).

①当a≥0时,f′(x)≥0,函数f(x)在(0,+∞)上单调递增,因为f(1)=a+1>0,当x→0时,f(x)→-∞,所以函数f(x)有1个零点;

综上可知,当a<-1时,函数f(x)没有零点;当a=-1或a≥0时,函数f(x)有1个零点;当-1<a<0时,函数f(x)有2个零点.
素养分析3:函数f(x)零点的个数就是f(x)=0的解的个数,等价变形为lnx=-ax-1,进而转化为直线y=-ax-1与函数u(x)=lnx的图像的交点个数问题,运用数形结合思想来解决,其解决过程要注意“脑中有‘形’,心中有‘数’”,进而探寻事物变化规律,这也是直观想象、数学运算等核心素养的考查.
方法2:函数f(x)的定义域为(0,+∞),由f(x)=ax+lnx+1=0,得lnx=-ax-1.
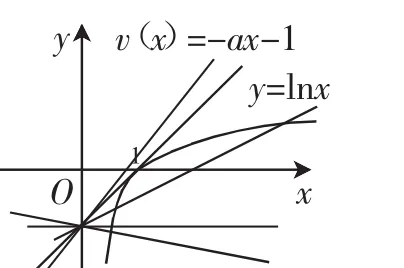
图1
令u(x)=lnx,v(x)=-ax-1,则函数v(x)是过定点(0,-1),斜率为k=-a的直线,而函数u(x)的图像如图1所示,当直线y=kx-1与函数u(x)=lnx相切时,两者只有一个交点,此时设切点为P(x0,y0),则的图像的交点个数,只要借助于导数把函数g(x)的图像正确地画出来,自然一目了然.这是考查数学抽象、直观想象等核心素养,促进学生思维能力、实践能力的发展.
方法3:函数f(x)的定义域为(0,+∞).x0=1,k=1,y0=0.
所以当k>1时,函数f(x)没有零点;当k=1或k≤0时,函数f(x)有1个零点;当0<k<1时,函数f(x)有2个零点.
所以当a<-1时,函数f(x)没有零点;当a=-1或a≥0时,函数f(x)有1个零点;当-1<a<0时,函数f(x)有2个零点.
素养分析4:函数f(x)零点的个数问题也可以应用变量分离法转化为水平直线与函数图像的交点个数问题来处理,形象直观,本题是转化为直线y=a与函数g(x)
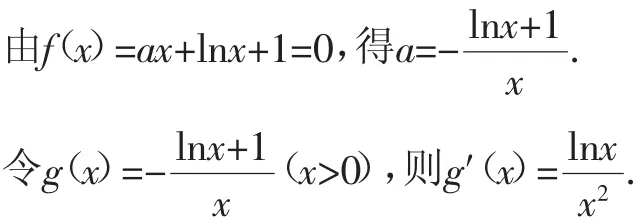
因为当0<x<1时,g′(x)<0,当x>1时,g′(x)>0,所以函数g(x)在(0,1)上单调递减,在(1,+∞)上单调递增,g(x)min=g(1)=-1.
所以当a<-1时,函数f(x)没有零点;当a=-1或a≥0时,函数f(x)有1个零点;当-1<a<0时,函数f(x)有2个零点.
三、函数零点的问题的基本活动经验
函数零点的问题的求解策略有如下的方法:
(1)特征分析,分类讨论.
应用导数的正负研究函数的单调性,运用分类讨论思想,有逻辑地表达与交流,进而利用零点存在性定理进行探索.
(2)部分分离,化为切线.
若函数可以等价变形为t(x)=k(x-x0)+b的形式,函数零点的问题即可转化为函数y=t(x)的图像与直线y=k(x-x0)+b的交点个数的问题,运用运动的思想探求问题,其中参数取值范围的临界值就是直线与函数图像相切时对应的参数值,而临界值的求解往往应用导数的几何意义来确定.
(3)完全分离,函数最值.
分离变量法的主要思想是将函数零点的问题转化为一个一端是参数a,另一端是变量表达式v(x),进而应用数形结合思想探求水平直线y=a与函数y=v(x)图像的交点个数问题来解决.
以上通法各有利弊,须以函数的特征来合理选择.在求解过程中,力求“脑中有‘形’,心中有‘数’”.依托端点效应,缩小范围,借助数形结合,寻找临界.
四、提升数学核心素养的思考
从函数零点的问题的教学案例的核心素养分析可以看出,思考问题、解决问题的过程中用到的基础知识、基本技能和基本思想方法只有在具体问题的求解时才能发挥作用,经历审视、分析、转化与化归的过程也就是积累基本活动经验的过程,而在问题的求解中起决定性作用的却是六大核心素养[5].
数学学科核心素养的三个方面,六个关键词,既相对独立,又相互交融,是一个有机的整体.首先,学生从外界输入信息,亦即用数学的眼光观察世界,发展数学抽象、直观想象素养;其次,学生处理信息,亦即用数学的思维分析世界,发展逻辑推理、数学运算素养;再次,学生输出信息,亦即用数学的语言表达世界,发展数学建模、数据分析素养.
数学课堂教学的基本任务是带领学生螺旋式地透彻理解一个个的数学知识,并引领学生结合试题的背景、应用的情境提出问题、思考问题,进而利用自身的知识储备解决问题,这是实实在在的事情.这样,在平时的数学教学设计中思考落实数学核心素养的意识,在数学课堂教学各个环节中探寻发展学生数学核心素养的途径,在教学反思中矫正提升学生数学核心素养的策略,且教学且思考,应成为我们数学教学思考的最基本的追寻点.
