学习进阶：思维课堂从形式走向本质*

☉江苏省宜兴市丁蜀高级中学 赵 平

☉江苏省宜兴市丁蜀高级中学 徐 静

一、问题背景

近十年，中小学课堂改革行动可谓如火如荼，“学为中心，以学定教，还课堂于学生”的理念唱响课堂教学的主旋律，众多新课堂模式应运而生.纵观这样的课堂，最突出的变化在于限定教师的讲授时间：不超过30或20分钟，更有甚者规定不超过15分钟，好像教师讲的越少或者不讲，课堂就显得越生本、越高效，教师的地位在逐步边缘化.无视学情，忽略内容，盲目求同，试图通过对课堂时间分配“一刀切”最大限度凸显学生的主体地位，这样的改革真的能促进学习成效吗？

笔者认为，课堂是生活的，生态的，生命的，是教师、学生、教学素材、教学媒体以及所处环境等多元要素交互作用的共同体，削减或严控教师讲授的时间，未必会真正激发学生的主观能动性，倘若教师真的退出历史舞台，那么课堂将变得更浅薄.反观当前课堂改革现状，有些方面存在异化的趋势：（1）改革者聚焦于学生的显性行为，有无小组合作，有无示范演练，有无探究活动等，却无视学生的主观愿望，无视学生的思维发展差异；（2）过度强调学生的主体学习，忽视教师的有意义引导，试图以“学生的自主发现”替代“教师的有效启发”.这样的课堂依然是低效的，亟待改善.

学习进阶理论揭示学生在一个较大时间跨度内学习某一主题所遵循的持续连贯，逐步精致的思维路径.学习进阶刻画学习者由低认知层次向高认知层次发展的动态过程.教师可依据学习进阶理论探索“为学生设计怎样的学习路径”，促进学生的深度学习.思维课堂就是在学习进阶理念的引领下，学生自主发现和建构知识，师生互动合作解决问题的课堂.思维课堂一般包括旧知激活、问题驱动、自主发现、自主建构和学以致用五个操作环节，下面结合笔者在学校对外公开课中开设的一节微专题课——“探究椭圆中一类斜率之积为定值的问题”，谈些体会，以飨读者.

二、案例分析

（一）进阶起点

本节内容安排在高三一轮复习完成椭圆标准方程和几何性质专题复习之后，旨在提炼解析几何的解题策略，培育学生的数学素养.

进阶起点1：初中学生已对圆的几何性质比较熟悉，学生知道圆的直径所对的圆周角为直角，也能从动点对两定点的张角为直角判断动点轨迹为圆.

进阶起点2：学生从几何直观的角度对圆和椭圆的几何特征的相似性有一定的感性认识，了解椭圆可看成圆发生形变后的图形.

（二）进阶终点

引导学生通过“圆上任意一点与直径两端点连线斜率之积为定值-1”探究“椭圆上任意一点与过椭圆中心的弦的两端点连线斜率之积为定值”，认清解析几何中定值的代数本质，体会恒等原理和类比推理、特殊到一般的思想方法.

（三）进阶障碍分析

障碍1：学生对曲线的方程和方程的曲线缺乏深刻的认识，概念理解不严密.根据“动点到两定点连线斜率之积为-1”求动点轨迹时，学生忽视两线斜率存在且非零的隐含条件，从而在所求轨迹方程中没有除去两个定点，呈现思维定式负效应的影响.

障碍2：学生对类比圆中斜率之积为定值得出椭圆中相应的结论，只是流于形式和结果，对于形变引起的斜率变化缺乏本质认识，也未能用联系的观点看问题.

障碍3：学生能用坐标法证明椭圆中有关定值的结论，但只是程序化的模仿，缺乏对解析几何本质思想的认识，对证明定值的策略没有形成系统，无法灵活地迁移至新的问题情境中.

（四）学习进阶视域下的微专题片断

1.旧知激活设悬念

师：请同学们思考这样一个问题：已知平面内A，B两点的坐标分别为（-2，0）和（2，0），P为任意一动点，若kPA·kPB=-1，则点P的轨迹是什么样的曲线？

生1：应该是以AB为直径的圆，方程为x2+y2=4.

师（追问1）：请你再审视一下“kPA·kPB=-1”这个条件，觉得结果表达得准确吗？

生1：噢，还要考虑斜率存在，好像还不能为零，这样的话，还要去掉A，B两个点，所以曲线方程应该为x2+y2=4（x≠±2）.

师：很好，思维越来越严谨了.

师（追问2）：你是怎样得到这个结果的呢？

生1：我是从几何性质角度直接看出来的.

师（竖起拇指）：够厉害，你的几何直观能力很强！那么，还有更具体的判断方法吗？

师（追问3）：你对于kPA·kPB=-1的几何意义怎么看？

生2：首先说明PA⊥PB，进一步说明点P在以AB为直径的圆上，所以kPA·kPB=-1.

师（追问4）：很好，你能概括出一个一般性的结论吗？

生2：圆上任意一点对直径的张角为直角，与直径两个端点连线的斜率之积为定值-1.

进阶策略：故布疑阵设悬念——本节课题为“探究椭圆中一类斜率之积为定值的问题”，却偏偏从圆的问题引入，学生开始会存“疑虑”，但也激发了探明真相的好奇心.先行组织聚学情——“依据张角直角判断轨迹是圆”符合学生的原有的认知经验，给学生以亲切感.问题表征明细节——问题的关键节点“垂直”的翻译，通过层层追问，引发学生从角、斜率甚至向量多角度思考，对斜率存在与否的辨析，训练思维的严密性，从特殊到一般引导学生归纳结论，其中突出用斜率表示定值，为探究椭圆埋下暗线.

2.自主发现并建构

师：类比刚刚研究圆中的结论，大家觉得椭圆中是否也有相似的结论呢？首先，圆周角是固定的直角，那么椭圆上任意一点对长轴的张角也固定吗？

生4：不固定，会变化，感觉在短轴顶点处张角最大.

师（追问5）：角在变，PA，PB的斜率显然也在变，那么kPA·kPB的值变吗？

生4：不变，生3已经作出了证明.

师（追问6）：你能从椭圆方程中找到定值的线索吗？生4：应该和椭圆中的a，b有关.

师：想必大家心中已有猜测，那么对于一般的椭圆是否也有这样的性质？如何描述？如何证明？请大家自己尝试完成.

进阶策略：变式引申显联系——改变题设，揭示圆与椭圆的相似性，唤起学生对它们内在联系的关注与探究；问题驱动拓思维——用类比的方式铺设问题链，引导学生的关注点聚焦于斜率之积为定值这一在圆与椭圆中共有的性质，体现前后一致，思维连贯；适度留白彰生本——从特殊的逐步提炼到一般的严格推证，给学生留下尝试、反思、调整、分享的空间，课堂尽显生本味.

3.学以致用育素养

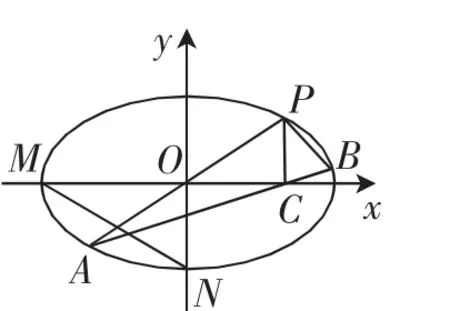
图1

证明：因为直线PA经过原点，所以可设P（x1，y1），则A（-x1，-y1），C（x1，0）.又因为B是椭圆上异于P，A的一点，所以可设B（x2，y2）.由“椭圆上任意一点与过椭圆中心的弦的两端点连线斜率之积为定值-”这一结论可

进阶策略：“垂直”表征合理化——此题为证明题，所证目标平面的“线线垂直”，由于表征形式多样，譬如：向量数量积为0、斜率乘积为-1，勾股定理，余弦定理等，如何合理表征，至关重要，需引导学生联系已知条件信息，结合几何图形特征，准确选择验证斜率乘积为-1；借用引理巧转化——唤醒学生的几何直观，关注特征点P，A的对称性以及B的任意性，化归椭圆圆周角性质定理的适用模型，巧妙；运算简化育素养——利用三点共线，结合中间结论，稍作代换，目标达成，运算量大大降低，充分发展学生的数学运算素养.

三、教学后记

学习进阶理论引领下的思维课堂通过契合学生最近发展区的问题情境激疑生趣，通过问题链及有效追问的环节为学生的学习内驱力指明发展的方向，通过类比推理来自主发现和建构体验核心概念的自然生成并灵活应用于新的题境，通过教师的角色转换和功能优化真正实现课堂从“教知识的讲堂”变为“化素养润思想的学堂”.当然，纵观课堂环节，一些细节处理仍有瑕疵，譬如，教师让学生归纳和推导椭圆圆周角性质定理前，对于椭圆上两动点关于中心对称这一位置没有指明，缺少进阶“支架”.又如，在课堂总结时，是否可以对斜率之积为常数的其他类型对轨迹的影响作一设问，如“斜率之积为正数时的曲线是什么”？这样，学生的研究性学习兴趣被调动，课堂的开放性和衍生性得以彰显.瑕不掩瑜，在落实五环节的过程中，只要尊重学情差异和学生内需，因材施教，动态生成，一定可以有效落实适合学生可持续发展的数学核心素养.