“学讲方式”下说题教学的思考*

☉江苏省泰兴市第三高级中学 陈 伟

“学讲方式”这一课堂教学方式的主要学习方式是自主学习，主要教学组织形式则是合作学习，这种引导学生“学进去、讲出来”并因此促进学习目标达成的教学方式对于改善课堂教学生态是极为有效的手段.学生在“学进去、讲出来”的过程中往往会变得更为主动和活泼，教学活动也会因此变得更具目的性、针对性和实效性，教师的教与学生的学也会因为过程的生动而更具实效性.

数学的产生与发展都是围绕问题而进行的，发现问题与解决问题的过程是数学学习最为主要的组成.能够突出数学问题和解题过程的说题能够将数学问题的衍生和辐射作用充分地展示出来.笔者结合“学讲方式”这一先进的课堂教学方式对说题这一环节谈谈自己的看法.

一、说题的意义

第一，“学进去”所包含的意义是多个层面的，对新知识的理解与掌握、新旧知识之间建立联系、有主动学习的积极情感、能够在主动学习中选择有效信息等内容均包含在“学进去”的范畴之中.因此，教师在实际教学中应帮助学生在掌握新知识的同时促进其新旧知识间联系的建立，引导学生学会贮存有效的知识信息并逐步形成乐意学习的态度与积极情感，使学生能够在知识点、能力点、兴趣点的结合处学会选择和处理信息.德国数学家莱布尼茨曾经对解题作过一定的解释，他认为既能展示思维过程、又能探索解的内部境界的解题才是成功的，而这正是完全可以在说题活动中完成的.因此，教师应善于引导学生在数学活动中主动计划、检验、调节与管理并因此使学生获得实现目标的能力.学生在说题过程中往往能够将自己的解题思想和过程充分地展现出来并在此基础上进行一定的调控与反思，这对于实际解题来说意义重大.

第二，“讲出来”所包含的意义自然也不是单一的，正确表达知识、归纳与概括知识、能为其他学生解疑等内容均是“讲出来”所包含的具体含义.因此，教师在实际教学中应引导学生在“学进去”的基础上将所学知识进行正确而清晰地表达，引导学生能够对所学内容进行归纳与概括并因此获得“教别人”的能力，这种内化知识并能将知识进行理解与表达的过程往往是建立在学有所悟的基础上的，这也是学生学习效果的一种反映与展现.因此，教师应为学生创造广阔的思考空间与思维外化的舞台并激发学生认知冲突的形成，使学生能够在解决冲突的过程中获得“高峰体验”并因此建构起良好的知识结构.说题活动对于学生知识结构的动态形成、学生的思维发展来说都是极其有效的途径.因此，教师应引导学生在问题的思考中进行自主学习、合作学习并表达出自己的观点，使学生能够在表达观点、交流切磋、论证归纳的过程中最终形成共识，使学生能够将所学知识顺利纳入原有的知识体系并令知识结构获得有意义的扩充.

说题活动包含了说题意、说思路、说思维过程、说解法、说反思等诸多环节和内容，说题包含的环节虽然不少，但说题者认真严谨的审题与充分思考是每个环节都必须具备的，教师在设计说题活动时可以从教材中、高考模拟试卷中、高考试题中选择有意义的素材.

二、说题前的准备

教师在落实说题活动之前首先应充分钻研教材并作全面而深入的分析，设计好预习内容并要求学生根据学习目标完成预习.学生可以以小组为单位进行资料的收集与整理、学习内容的预习等环节并因此准备好说题，个人或团队都是说题允许的模式.

三、说题的注意事项

作为说题教学组织者的教师对说题活动的干涉应做到适度，过多干预或过于放任都是极不合适的，教师在学生的说题过程中应做到适时、适度的点评与表扬.学生则应该在吃透学习目标的基础上充分理解题意并说出要点.学生说解题思路与方法的过程正是锻炼其表达能力、思维能力的过程，锻炼说题者自信心的同时也能令其他学生获得解题思维上的激发与拓展，共享解题乐趣的同时也能将学生的求知欲充分诱发出来.教师应鼓励学生大胆表达自身的个性化想法，只有这样，教师才能及时发现其错误并引导学生对自身的错误展开探索与修正.学生在说题过程中的思维碰撞往往能令其产生更多的灵感并促进学生交往的和谐融洽.学生在身心均感受到成功喜悦同时还能不断令自身的数学能力不断发展.

四、说题案例分析

（一）出题意图

这是一道融三角函数、函数与方程、不等式等诸多知识点于一体的综合题，不同知识点的融合交汇对于学生思维的灵活性与综合性均是一种挑战.

（二）说题中的思维中断

思路2：由函数解析式可得sin2x-2ysinx+4=0.

由Δ=（2y）2-4×1×4≥0，得y2≥4.

因为y＞0，所以y≥2.

同样y=2时，sinx=2也会成为可能，解题无法完成而导致思维中断.

（三）说解题过程

回顾上述的思维中断并进行探索可得以下解法：

解法1：由x∈（0，π），sinx∈（0，1］，

解法4：因为f（t）=t2-2yt+4=0（其中t=sinx，0＜x＜π）不仅有解，而且应在（0，1］上有解.

问题因此转化成了求抛物线v=u2（0＜u≤1）一段上一点和定点（0，-4）连线的斜率的最小值，

（四）说解题后反思

反思1：解题中应考虑不等式取等号的条件并在善于联想的基础上进行合理转化.

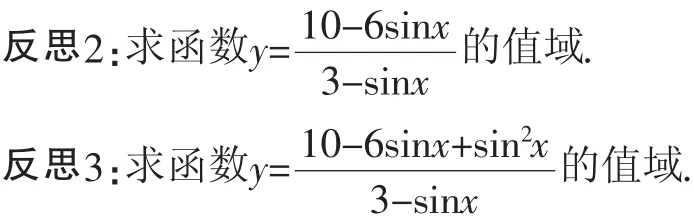
反思4：已知方程2sin2x-cosx-a=0有实数根，则实数a的取值范围如何？

（五）说拓展

从上述案例不难看出，说题活动所涉及的内容或许会有所改变，范围也或许有可能发生变化，但说题活动却能够将说题者的各方面能力均充分展露在大家面前.

总之，学生的学习过程与思维过程在说题教学的开展过程中都能得到充分的展现，学生的思维品质与严谨的学习态度也会在说题实践中得到有效的锻炼与发展，不仅如此，学生在形式多样的说题活动中往往会表现出浓厚的兴趣与较强的主动性并因此真正促成学生的“学进去，讲出来”，学生在充分表达自己观点或论证的过程中也真正实现了被动听讲到主动说讲的转变，学生的数学解题能力、数学交流能力、数学思维能力都会在这一过程中得到有力的提升并因此达成数学课堂优质高效的教学目标.W