基于灰色系统理论的快速时序数据挖掘算法

赵 颖

(青海广播电视大学 继续教育学院，西宁 810000)

近年来，伴随着计算机网络的不断普及，使得计算效率、存储容量、多机联合分析以及协助决策成为可能[1].因为没有便利的数据处理工具，人类对待处理数据已经无法处理[2],这就使得待处理数据在规模较大的数据库中变成“datatomb”，几乎不会被使用，决策一般没有方法使用这个容量较大的数据库，但是需要依靠制定者的直觉来做出决策[3-4].所以，使用先进的技术手段将数据转化成一种智慧，这是目前数据挖掘所要面对的新任务[5].MD算法是一种新兴的群体智能数据挖掘算法，该算法自身对目标函数的特性不存在具体的要求，它比较容易实现，同时具备较好的数据优化性能，已经是目前群体智能数据优化算法研究的重点，而此算法中使用随机数替换已找到的快速时序数据挖掘算法，这样会改变原来的数据造成误差，并且容易陷入局部最优[6].

快速时序数据挖掘算法实质是一种多个目标进行优化的局部数据挖掘算法，而对于一个比较复杂的矩阵来说，若使用快速时序数据挖掘算法对其进行数据处理，是不合适的.本文运用的方法主要是对整个数据进行全局优化的基础上，再寻找含有最佳子矩阵作为种子，然后对其运用快速时序数据挖掘算法.通过与快速时序算法和MDO算法进行比较可知：基于灰色系统理论的快速时序数据挖掘算法具有更好的全局寻优能力，且数据挖掘效果更佳.

1 数据挖掘算法

数据挖掘的问题是对隐含在数据中的价值信息进行有效识别，所谓的识别就是指具有相同特性数据的集合.因为相同数据特性的不同表达，所以对于数据可以使用不同的挖掘算法，例如可以距离来对数据相似性进行描述，此方法称之为距离的数据挖掘算法.通常来说，对于数据相似性的描述主要是数据挖掘者进行定义的.

一个比较好的数据挖掘算法可以对数据进行有效的挖掘，进而使得不同性质的数据的相似性降低，但是在相似性较高的数据内部，本文提出了一种应用于数据挖掘的算法.目前的研究重点主要是依据基本的数据挖掘模型，使用相应的数据挖掘算法来进行有效数据挖掘，而数据挖掘算法是一种具体的、确定的数据均值算法.它的主要思想是如果相似特性的数据确定后，那么数据的集合平均数也随之确定.进行数据挖掘之前需要确定数据挖掘的中心，而数据挖掘算法中心的选择是随机的，这种随机选择的方法使得数据挖掘算法的效率大大降低，即数据挖掘算法的迭代次数增多，使得CPU数据处理时间延长.因此，本文提出了一种改进的初始数据选择方法.

对于一个m行n列的矩阵A，AIJ为A的一个子矩阵，其中I为行(数据)的子集，J为列(条件)的子集，若AIJ的均方残差值满足一定的条件，则称AIJ为一个快速时序数据挖掘算法.其中，均方残差的计算公式为:

(1)

其中，aij为AIJ的有效元素，aiJ、aIj和aIJ分别为行平均值、列平均值和矩阵平均值.

2 基于灰色系统理论的快速时序数据挖掘算法

2.1 快速时序数据挖掘算法

基于灰色系统理论的快速时序数据挖掘算法中已知数据表达矩阵A=(X，Y)，在使用欧几里德距离作为相似性度量的基础上，对数据集合进行划分，使所得到的数据挖掘划分能使总体类间差异(TWCV)最小.

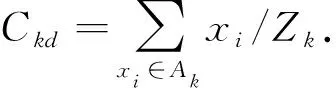
(2)

则TWCV可以表示为:

(3)

那么此适应度函数主要是各个挖掘数据同类中的函数WCV之和，如果WCV数值变小，则表示类内的每个对象相互之间比较亲密，也说明数据挖掘的效果很好.

基于灰色系统理论的快速时序数据挖掘算法，可以在全局数据挖掘和局部数据挖掘之间进行切换，增强了在多峰优化问题中寻找全局最优解的概率.粒子基于灰色系统理论的快速时序数据挖掘算法度量的公式如下:

(4)

(5)

其中，S表示挖掘数据，|L|表示求解空间最长对角线的长度，N表示问题的维数.

在基于灰色系统理论的快速时序数据挖掘算法中，单个粒子的收敛性是受收敛-发散因子β控制的.粒子进入收敛状态，种群的基于灰色系统理论的快速时序数据挖掘算法减小；粒子进入发散状态，种群的基于灰色系统理论的快速时序数据挖掘算法增多.挖掘数据在初始化后会进入收敛状态，这时β会从1.0线性减小到0.5，如式(6)所示.

(6)

将表达式(1)用作进化方程的MDO方法中，每个粒子收敛的充要条件需要满足β<1.782.所以存在β0=1.782，当β<β0时，粒子收敛；当β≥β0时，粒子进入发散状态.

2.2 灰色系统理论下的快速时序数据挖掘算法

基于灰色系统理论的快速时序数据挖掘主要实现两个任务，其一是快速时序数据挖掘算法下的剩余参数应该尽量取最小值；其二是快速时序数据挖掘算法需要的数据处理存储空间需要最大.但在灰色系统理论下的数据挖掘算法运行速度的参考只是存储空间能够变大，如果出现一组初始化比较大，那么可以认为此次运行执行是有效的，迭代需要不断进行，这显然是不合适的.

使用评估函数F(k，A)来评价灰色系统理论下的快速时序数据挖掘算法在每次迭代过程中的数据，F(k，A)的计算公式表达如下:

(7)

F(k，A)代表初始矩阵A的第k个快速时序数据挖掘阵的效果，rk表示平均平方差，vk表示容量，λ1和λ2依次表示均方残差和容量的权值.F(k，A)的数值变小，就表示这个快速时序数据挖掘算法矩阵的质量越好；相反，F(k，A)的值越大就表示这个快速时序数据挖掘算法矩阵的质量越差.

3 实验及分析

3.1 实验数据与环境

为了能够评估快速时序数据挖掘算法的效果，使用均方残差(MSR)、矩阵规模(V)以及行变动值(Var)来表达挖掘数据的一致性.目标是找到的快速时序数据挖掘算法均方残差要尽可能小，规模和行变动值要尽可能大.行变动值(Var)的计算方法如式(8)所示.

(8)

本文进行的实验选用的数据是急性白血病数据表达(Leukaemia)数据集和酵母菌数据表达数据集(yeast).选用的急性白血病数据一共有38个样本共7 129个数据.在这些数据中已经含27个患有急性淋巴性白血病(ALL)，11个患有急性骨髓性白血病(AML).因此，该数据挖掘算法主要分为两类.酵母菌数据集包含2 884个数据，17个样本.标准类的划分主要是按照数据达到峰值的时候运行的，这些数据全部是单独运行到峰值，细胞周期全部分为5个时相，因此把这些数据划分为5个标准类.实验在装有Win10系统的PC机上运行，CPU为Intel酷睿i5，4 G内存，实验环境为MATLABR2014a.

3.2 实验结果分析

将SSKMCA、MDO、本文算法，以及未改进的快速时序数据挖掘算法进行比较.挖掘数据规模为40，迭代次数300次；将急性白血病数据集聚为两类，酵母菌数据集聚为五类；通过实验确定公式(7)中参数λ1取1，λ2取1.8；d_low设置为0.000 5.

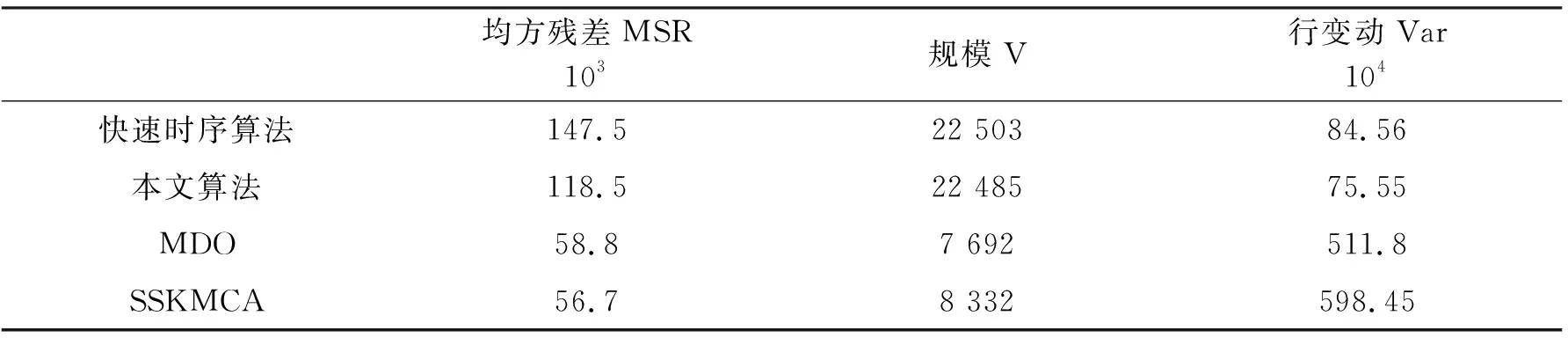
表1 四种算法在Leukaemia上的实验结果

表2 四种算法在yeast上的实验结果

表1、表2分别是快速时序数据挖掘算法、本文算法、MDO算法和SSKMCA快速时序数据挖掘算法在两个数据集上10次实验的平均值.

从表中前两行可以看出，本文算法的均方残差值比快速时序数据挖掘算法分别减小了19%和6%，改进后的本文算法虽然在规模上略有减小，但相差不大.所以用了本文算法表现结果更佳；从表中后两行可以看出SSKMCA和MDO算法的均方残差值相较于快速时序数据挖掘算法有明显减小，主要是因为此算法对待挖掘数据进行划分，在复杂的数据中划分为不同的表达浮动比较相近的数据模块，去除没有关系的外部干扰数据，当然这也导致了在第二阶段得到的数据挖掘矩阵的容量有所减少，但是和本文算法相比，得到的数据挖掘矩阵相似性更集中，总体上质量有很大幅度提高；本文算法和MDO算法相比，虽然规模相差不大，但是本文算法均方残差明显减小.说明本文算法相较于MDO算法在性能上有所提高，数据挖掘效果更佳.

4 结语

数据挖掘繁杂且没有规律，针对此问题，提出了一种基于灰色系统理论的快速时序数据挖掘算法.该算法根据灰色系统理论的快速时序数据挖掘算法判断数据状态，以提高算法的全局数据挖掘能力；再结合基于灰色系统理论的快速时序数据挖掘算法，修改其迭代目标函数，弥补了基于灰色系统理论的快速时序数据挖掘算法在处理多目标优化问题时的不足.经过实验证明，本文提出的算法具有较好的全局寻优能力，且数据挖掘效果更佳.