对一道高考三角试题的探究

宁夏彭阳县第三中学(756599) 王伯龙

题目(2018年江苏省高考数学第13题)在△ABC中,角A、B、C所对的边分别为a、b、c,∠ABC=120°,∠ABC的平分线交AC于D,且BD=1,则4a+c的最小值为___.

这是一道考查解三角形与最值的综合题,试题涉及到三角形中定角及定角的平分线,边长之间关系的最值问题.试题设置新颖、寓意深刻、情境熟悉、情态鲜活、解法多样,采用“以能力立意”的命题思想,注重新旧知识的交汇,着力考查知识和技能的应用能力和迁移潜质,是一道值得研究的好题.

1.试题的解法研究

著名数学家、教育家G·波利亚说：“掌握数学就意味着善于解题.”单墫先生也说过：“学数学的目的,不是别的,就是为了学会解题.”因此,用什么方法能顺利解答问题是最务实的,是数学素养和综合能力的体现.上等方法简洁明快,手到“病”除,而中、下等方法耗时费力,甚至陷入误区.武向义先生说：“教数学要交给学生‘大巧’,要教学生‘运用之妙,存乎一心’,以不变应万变.”可见,不同的方法展现不同的数学思维水平.这正是体现高考试题的选拔功能.

解法1(面积法)因为S△ABC=S△ABD+S△BCD,所以,即.于是9,当且仅当,即c=2a时取等号,故4a+c的最小值为9.

解法2(向量法)因为BD是∠ABC的平分线,所以可设,两边分别与自身作数量积并化简整理得,以下同法1,故当c=2a时,4a+c的最小值为9.

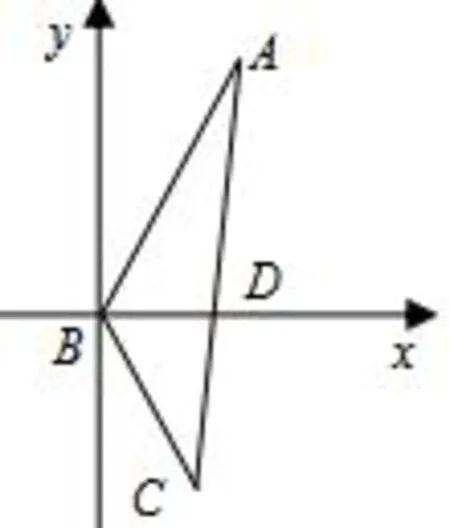
图1

解法3(坐标法)如图1,以B为原点,BD所在的直线为x轴建立平面直角坐标系,易得D(1,0)、,由于A、D、C三点共线,因而有,即,化简得ac=a+c,以下同法1,故当c=2a时,4a+c的最小值为9.

解法4(张角定理法)由张角定理得

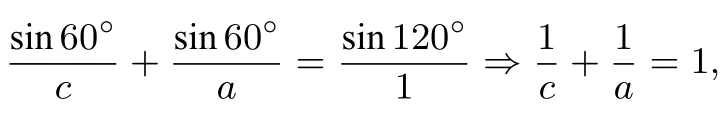
以下同法1,故当c=2a时,4a+c的最小值为9.

注张角定理：△ABC中,D为AC边上一点,连接BD,则.

评析本题求4a+c的最小值的关键是通过题目的已知条件,利用不同的思维方法找到a、c之间的关系,然后利用基本不等式求解.

由解法4,我们可以体会到这道高考试题是以张角定理为背景来命制的,而考题只是特殊情形下的一道试题,我们可将试题一般化进行推广.

2.试题的推广

结论1在△ABC中,角A、B、C所对的边分别为a、b、c,∠ABC=θ,∠ABC的平分线交AC于D,且BD=t,则λa+µc(λ＞0,µ＞0)的最小值为.

证明 由张角定理得,

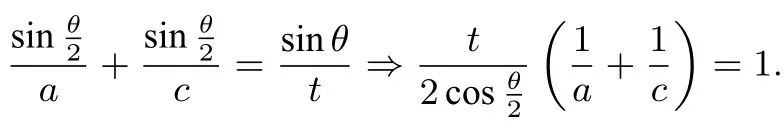
所以

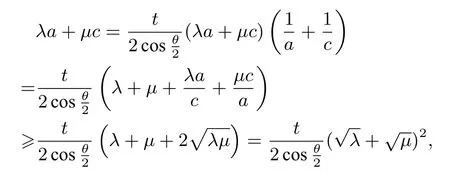
显然,当λ=4,µ=1,t=1,θ=120°时,便是考题的结论.

3.试题的变式推广

正如数学教育家波利亚所说：“没有一道题是可以解决得十全十美的,总剩下些工作要做,经过充分的探讨与研究,总会有点滴的发现,总能改进这个解答,而且在任何情况下,我们都能提高自己对这个解答的理解水平.”他打比方说：“在你找到第一个蘑菇(或作出第一个发现)后,要环顾四周,因为它们总是成堆生长的.”通过试题的变式可以挖掘试题的内涵,体现试题的教学价值.数学的魅力在于“变”,有“变”才有“用”,有“变”才有“活”.

在考题的条件下,∠ABC的对边AC也在变化,那么,AC是否也有最小值呢?经过尝试探究我们便有如下的结论.

结论2在△ABC中,角A、B、C所对的边分别为a、b、c,∠ABC=θ,∠ABC的平分线交AC于D,且BD=t,则.

证明由张角定理得

取等号当且仅当a=c.又由余弦定理得AC2=a2+c2-2accosθ,结合不等式得

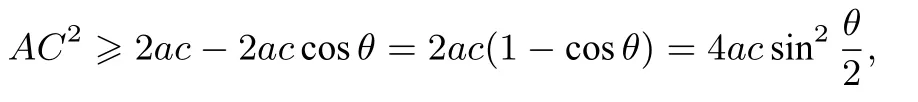
取等号当且仅当a=c.由式①得,

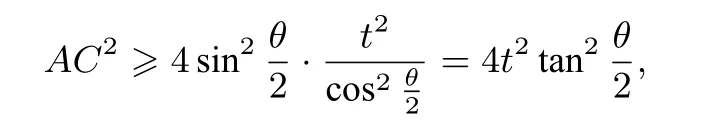
如果将∠ABC的平分线换成中线、高线,是否也有类似的结论呢?经过尝试探究我们便有如下的结论.

结论3在△ABC中,角A、B、C所对的边分别为a、b、c,∠ABC=θ,D为AC边上的中点,且BD=m,则当;当θ=90°时,|AC|=2m;当 90°＜θ＜180°时,.

证明当θ=90°时,由直角三角形的性质易得时,由中线向量得两边分别与自身作数量积并整理得

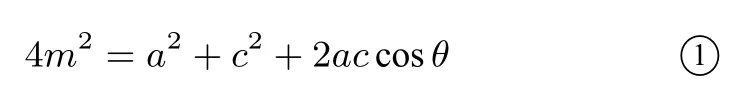
又由余弦定理得②-①得

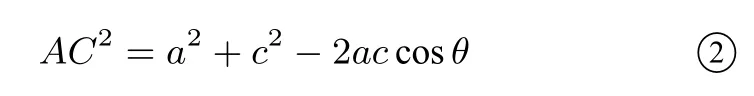
当然,我们也可将定线(中线、角平分线、高线)换成定周长、定面积等进行研究,限于篇幅,本文不再赘述,有兴趣的读者自行研究.

4.结束语

高考试题是命题专家集体智慧的结晶,是知识与能力的拓展,方法与思维的提升,随着新课程改革向纵深方向发展,研究的逐步深入,高中数学高考试题不断推陈出新,给高中数学教学带来了一波又一波的冲击.面对新的挑战,作为学生领路人的教师应主动涉水,潜心研究,这样才能在高中数学教学中高屋建瓴,有的放矢,才能确保对学生的指导方法得当,条理清楚,思路流畅.