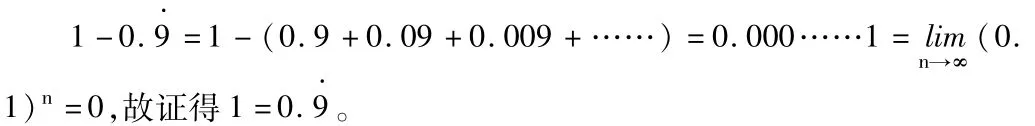用多种方法证明循环小数0.等于1
2018-11-15戴凡浩
中学课程辅导·教学研究 2018年29期
◎戴凡浩
自学了等比数列之后,循环小数皆可以使用无限多项的等比数列之和进行表示。例如:
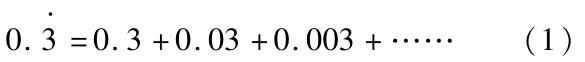
等式(1)中,等比数列{0.3,0.03,0.003,……}的公比 q为0.1,首相a1为0.3,故此等比数列的无穷多项和S求和公式为:
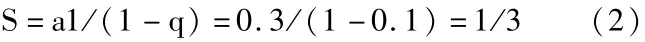
通过上面的方法,可以将所有的循环小数变成分数。
一.循环小数0.的分数形式
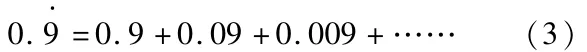
等式(3)中,等比数列{0.9,0.09,0.009,……}的公比 q为0.1,首相a1为0.9,故此等比数列的无穷多项和S求和公式为:
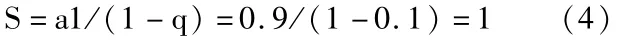
二.证明方法2:
将分数1/3分解为循环小数为:
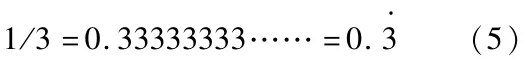
等式(5)两边都乘以3,等式左边1/3*3,为1;等式右边,为;即为:,证明完毕。
三.证明方法3:
将分数1/9分解为循环小数为:
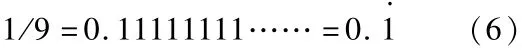
等式(6)两边都乘以9,等式左边1/9*9,为1;等式右边,为;即为:,证明完毕。
四.证明方法4:

等式(7)两边都乘以10,则:
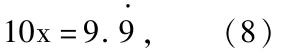
等式(8)减(7),得:
五.证明方法5:
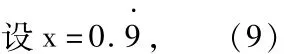
等式(9)两边都乘以0.1,则:

等式(9)减(10),得:
从而证得0.9·=1。
六.证明方法6:
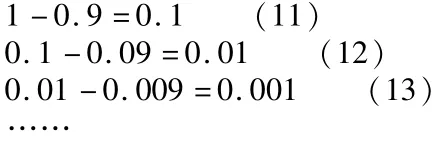
将无限多个上面的等式累加,结果为:
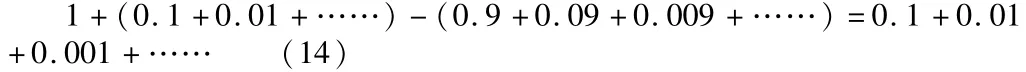
证明完毕。
七.证明方法7:
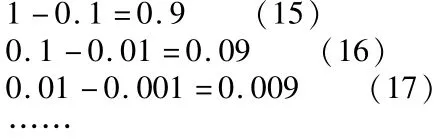
将无限多个上面的等式累加,结果为:
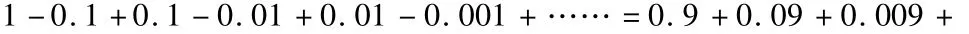

等式左边只会留下1,其余0.1、0.01、0.001等小数会与随后的相反数 -0.1、-.01、-0.001所抵消,故等式左边简化为1;而等式右边可以简化为,代入等式(18),即为:
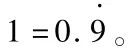
证明完毕。
八.证明方法8:
设
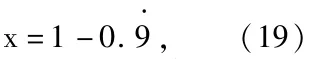
等式(19)两边都除以9,则
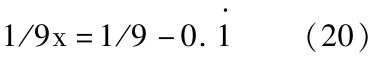
九.证明方法9: