超声换能器表面振动和声场测量及其与经典超声换能器的仿真比较

孙彦招，张涛



超声换能器表面振动和声场测量及其与经典超声换能器的仿真比较

孙彦招，张涛

(天津大学电气自动化与信息工程学院，天津 300072)

超声换能器广泛应用于声学测量，其工作性能主要取决于它的振动与声特征。然而，多数研究中的换能器被认为是经典的活塞或高斯型，经典与常用的真实换能器之间的差异容易被忽视。基于此，首先用激光测振和传声器测声方法测量了某厂家换能器产品的表面振动与声场特征。然后设计有限元方案，分别仿真经典与真实换能器的声场。最后从辐射面振速分布、声场声压和相关系数等方面，综合比较经典与真实超声换能器之间振动与声场的异同。结果表明，换能器间的辐射面振速分布差别明显，所研究的真实换能器的声场特征接近于活塞，而与高斯型差别较大。

超声换能器；振动测量；声测量；有限元方法；声场

0 引言

超声换能器广泛应用于测量领域。换能器表面的振动形态及辐射出的声场分布直接影响其工作的准确度和可靠性，因此研究这两方面具有重要意义。学者从实验和仿真两方面进行了研究。

对于实验，Sapozhnikov等[1]用激光测振仪测量了方形压电片表面的振动特征，并用声全息法构造了近场区的声场特征。Jimenez等[2]用Labview软件编写了压电换能器振动测量的数据处理和实验结果可视化程序，展示了换能器表面不规则的振动形态。Kluk等[3]搭建了用于超声换能器参数估计和状态诊断的测量系统。金士杰等[4]用光弹法测量了超声换能器的瞬态和稳态的辐射声场特征。

对于仿真，2009年，Clayton研究了虚拟的复合式压电换能器的电、声和力耦合场，得到了发射电压峰值处换能器的辐射声压等值线图[5]。2011年，Rahani等[6]对有限尺寸的平面圆形换能器发射的超声波声场进行了分析。2012年，Martins等[7]对活塞型超声换能器的单层和多层厚度模态进行了优化，讨论了厚度、共振频率和结构对换能器输出声压值的影响。2014年，刘雪林等[8]讨论了活塞型超声换能器发射频率和换能器尺寸对声场分布的影响。

通过文献分析发现，近些年学者在超声换能器实验和仿真研究方面做了很多工作，取得了许多成果。但在仿真时，研究者将重点放在内部力电声耦合[5,7,9-10]或经典换能器(以下指活塞型或高斯型换能器[11])上[5-8]。对于设计、制造、材料、使用环境和使用时间等因素[1-3,11-12]导致的真实换能器表面振动形态和辐射声场特征，还需继续研究。而在实验测量真实换能器时，与仿真的结合、定量比较等方面也需进一步研究。

基于此，为了比较某厂家的超声测距换能器产品(以下简称真实换能器)与经典换能器的异同，进行了如下的工作。首先设计含激光测振和传声器测声的实验方案，实测换能器的表面振动和声辐射特征。然后借助COMSOL软件设计仿真方案，分别仿真经典与真实换能器的声场。最后分别验证经典和真实换能器的声场仿真准确度。同时从换能器表面振速分布、声轴线声压和相关系数等3方面，综合比较真实与经典超声换能器振动与场的异同。

1 换能器的振动与辐射声场的测量

1.1 实验方案

使用某厂家生产的超声测距换能器时，为判断其是否属于经典的活塞型或高斯型换能器[11]，设计了表面振动和辐射声测量的实验方案。

换能器辐射表面振动测量系统见图1，它主要由1#和2#两个圆柱形PZT5压电陶瓷复合换能器(同型号、同批次产品)、换能器激励电路和Polytec PSV-400-3D型非接触式激光振动测量仪等组成。换能器激励信号为任意常用的峰峰值为336 V和434 V、频率为36.18 kHz的正弦波。测振仪用来检测换能器辐射表面的振速，频率测量范围0～1 MHz。对换能器表面L1至L8线上的81个点进行逐点扫描，见图2。

声测量装置见图3，它除了用振动测量系统中的超声换能器、换能器激励电路外，还用了三维移动定位系统、传声器及前置放大器、示波器。三维移动定位系统的最小分辨率为0.05 mm。传声器为预极化驻极体测试电容式，频率范围为0.02～70 kHz。示波器带宽为100 MHz、采样率为1.0 GHz。为了避免高频率声源辐射时，声场测量布点多、任务量大的特点，测量只在过换能器辐射表面中心的轴上进行。在此中心轴上，0～300 mm距离内以每5 mm的间隔来测量声压值。对于振动和声场测量，每个点均测量5次。

图1 换能器表面振速测量系统

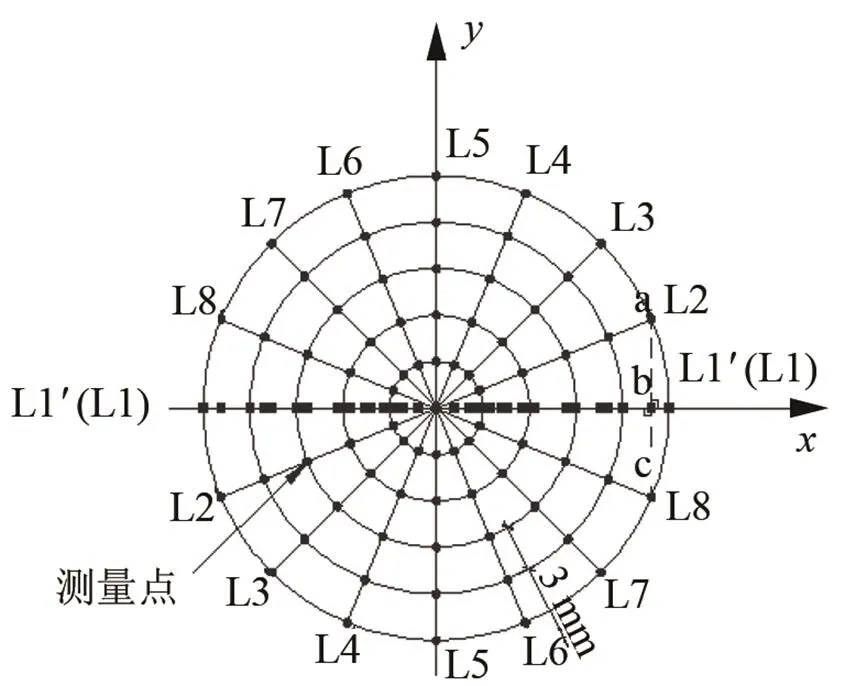
图2 换能器表面的振速测量点及其投影示意

图3 换能器的辐射声场测量系统

1.2 实验结果分析方法

首先分析振速数据。振速信号的波形见图4，横、纵坐标分别是时间和速度。

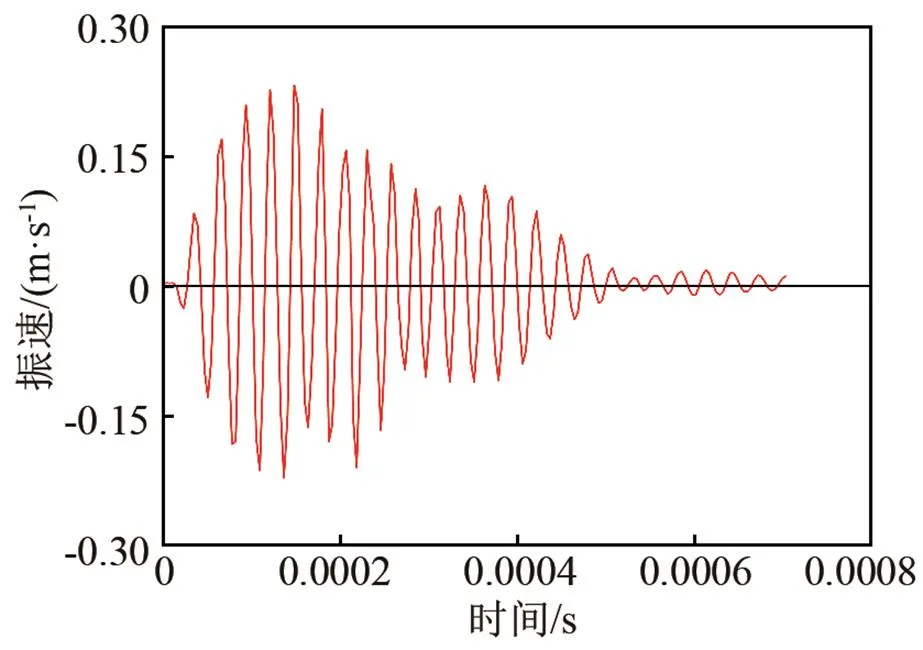
图4 换能器表面测量点的振动信号波形

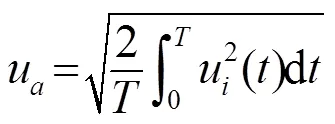
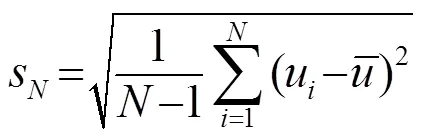
2 换能器辐射声场的仿真

2.1 经典换能器的仿真方法

在经典换能器仿真时，使用与真实换能器相同的几何尺寸、共振频率和表面振速幅值等参数，以便与真实换能器进行比较。用有限元法求解换能器声场，方案如下。

2.2 真实换能器的仿真方法

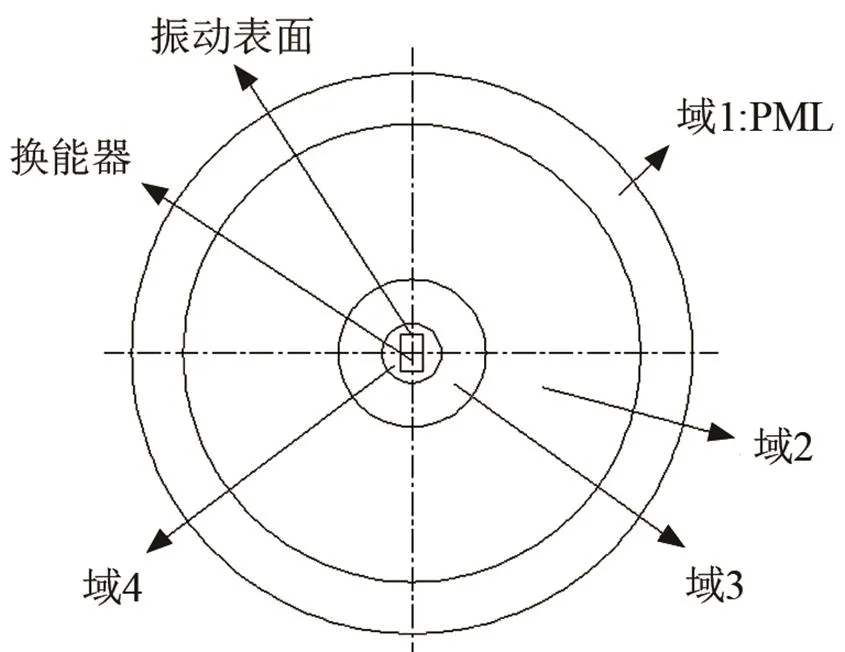
图5 换能器的几何体和求解域

3 真实与经典换能器的结果比较

3.1 换能器声场仿真的验证

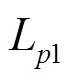
计算结果如表1所示。由表1可知，两类经典声源SPL的解析解与有限元解的最大和最小误差分别为0.09%和-0.10%。

然后，将仿真值与实验值进行比较，验证真实换能器的仿真正确度。图6显示了声源轴线上不同位置处仿真和实验结果的比较。对于3组仿真-实验情形，在0～0.025 m范围的换能器附近，相对误差范围为-2.75%～-0.15%。在0.05～0.29 m的范围，因声能分布随距离的增大而发散，仿真和实验值都随距离的增加而迅速减小。最大相对误差1.16%出现在“1#换能器434 V”的情形。当距离大于0.29 m时，仿真值突然下降，这是因为仿真时此区域处于声波吸收作用强的完美匹配层(Perfect Matched Layer, PML)中。

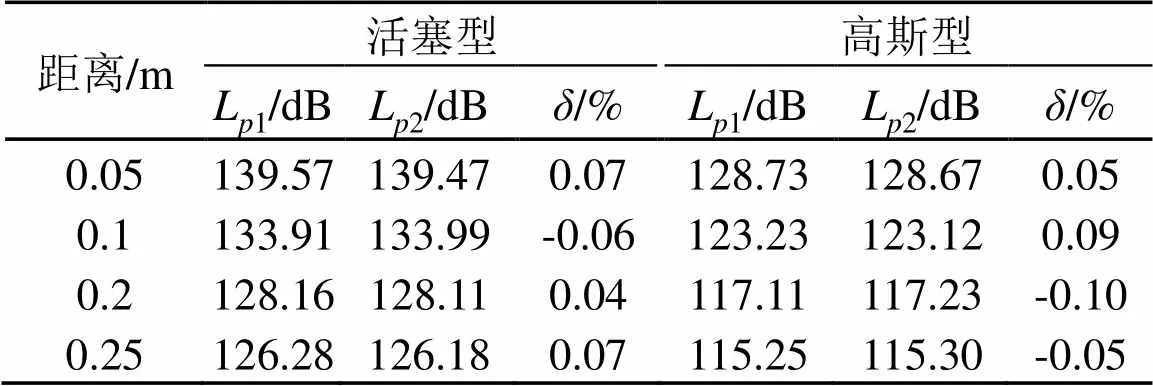
表1 经典换能器轴线上声压级的仿真值与计算值比较

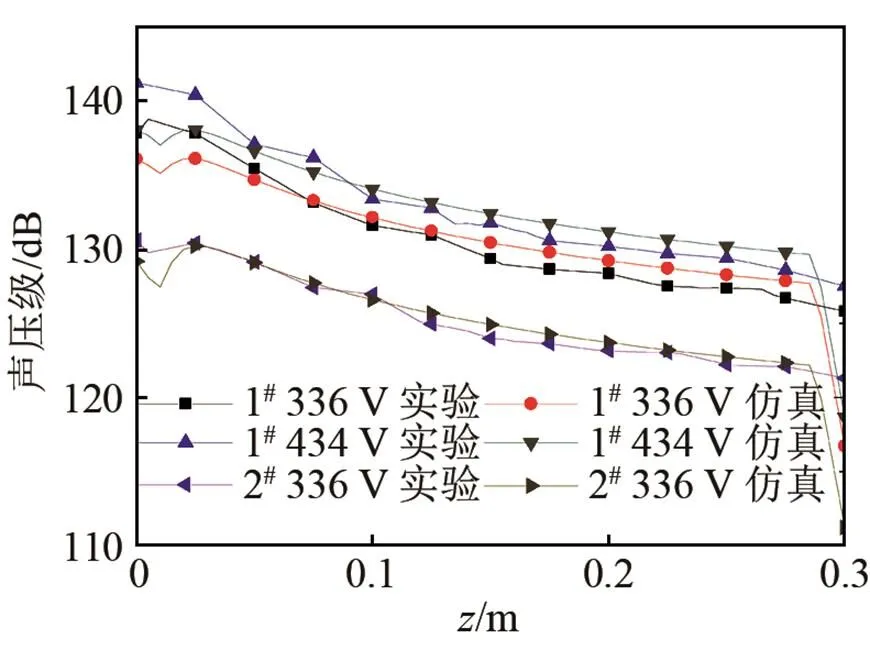
图6 真实换能器中心轴线上声压级的仿真值与实测值比较

通过换能器的仿真和对比可知，有限元解、解析解以及实验值具有良好的一致性，说明了仿真方案是可行的。

3.2 换能器表面振动形态的比较

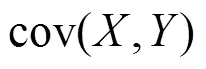
图7 经典与真实换能器辐射面的振速分布

Fig.7 Vibration velocity distributions on the radiation surfaces of classic and real transducers

表2 换能器表面振速分布的相关系数

3.3 换能器振动辐射声场的比较

图9显示了经典和真实两类换能器辐射声场的声压级分布。由图9(a)、9(b)可知，活塞声源的声场在近场具有空间的不均匀性，而在远场具有旁瓣辐射；高斯声源的声场中无旁瓣，声场分布呈高斯规律。

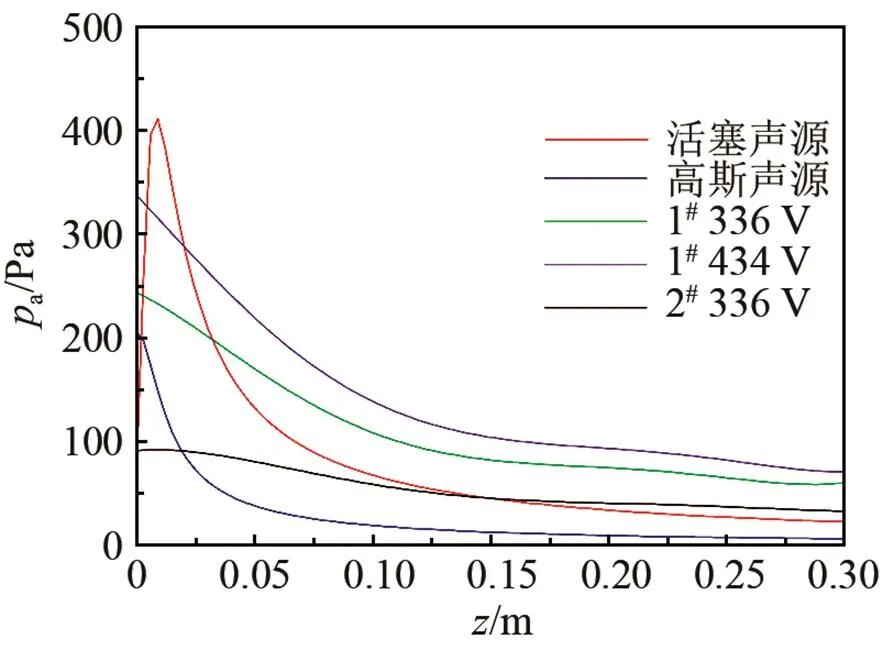
图8 经典与真实换能器声场轴线上的声压幅值比较

图9 仿真得出的经典与真实换能器声场分布

图9(c)～9(e)显示了1#和2#换能器的模拟声特征。由图9可知，声场中有1个主瓣和4个旁瓣，主瓣集中了声场的大部分能量。对于1#换能器，在2种电压下，主瓣宽度和形状相似，但与2#换能器有小的差别。对于1#换能器，激励电压越大，声场声压越大。而对于不同的换能器1#和2#，在相同的激励电压下，1#换能器的声场大于2#换能器声场的最大值和最小值。

图9(c)～9(e)与图9(a)～9(b)相比较，可以发现，声场中主瓣和旁瓣的形状和数量，随换能器类型、激励电压的变化而存在差异。以上的定性结论也可从各声场的相关系数(见表3)中得到定量证实。

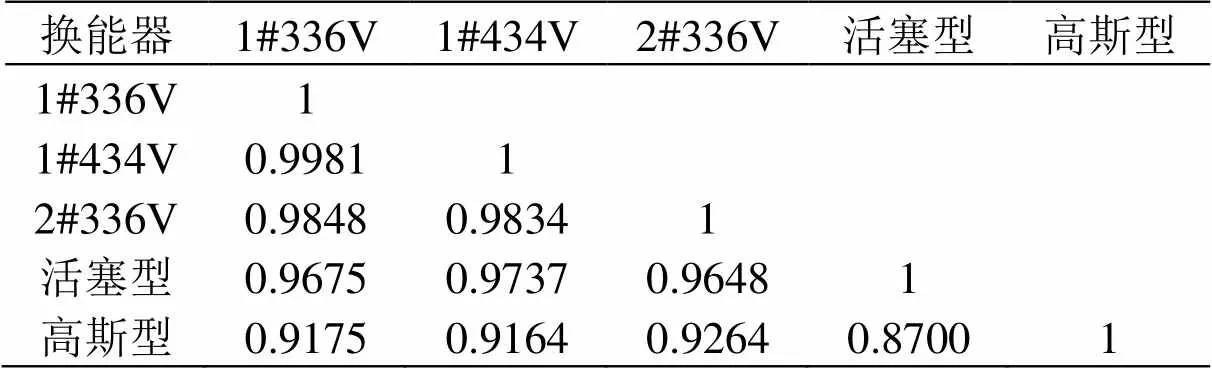
表3 换能器声场分布的相关系数

4 结论

用经过验证的仿真和实验方案，分析了某厂家换能器产品的振动和声辐射特征，并与经典换能器进行比较，结论如下。

(1) 表面振速分布。通过激光测振和换能器测声实验发现，真实换能器的表面振速分布呈不均匀和非对称性，可以用高次多项式来拟合振速分布，不同于经典换能器的常数或高斯函数。通过相关系数分析发现，各换能器之间表面振速分布的相似度，随换能器类型、激励电压的变化而存在显著的差异。对于同一个真实换能器，在不同的激励电压下，振速分布的相关度较高。

(2) 声场分布。对于换能器中心轴线的声压变化，通过实验测量和仿真发现，在换能器的近场和远场，相同距离处、不同类型换能器的声压差异较大，近场区声压值变化趋势和数值的差异更大。对于声场分布，根据相关系数分析发现，换能器之间声场分布的相关度，也随换能器类型、激励电压的变化而存在差异。相同换能器在不同的激励电压下，声场分布的相关度高。

总之，由于设计、制造、材料、使用环境和使用时间等因素，会使真实换能器与经典换能器之间的振动与辐射声特征存在差异。此外，所述的仿真、测量和分析方法，可以为研究者进一步精确分析工程和科研应用中换能器的振动及声辐射特征提供参考。

[1] SAPOZHNIKOV O A, MOROZOV A V, CATHIGNOL D. Piezoelectric transducer surface vibration characterization using acoustic holography and laser vibrometry[C]//Montreal: IEEE Ultrason Ferroelect & Frequency Control Soc, 2004, 161-164.

[2] JIMENEZ F J, FRUTOS J D. Virtual instrument for measurement, processing data, and visualization of vibration patterns of piezo- electric devices[J]. Computer Standards& Interfaces, 2005, 27(6): 653-663.

[3] KLUK P, MILEWSKI A, KARDYS W, et al. Measurement system for parameter estimation and diagnostic of ultrasonic transduc- ers[J]. Acta Physica Polonica A, 2013, 124(3): 468-470.

[4] 金士杰, 安志武, 廉国选, 等. 光弹法测量超声换能器声场[J]. 应用声学, 2014, 33(2): 107-111.

JIN Shijie, AN Zhiwu, LIAN Guoxuan, et al.Photoelastic quantification of ultrasonic beams radiated by transducers[J]. App- lied Acoustics, 2014, 33(2): 107-111.

[5] CLAYTON L. Fishing with Multiphysics[EB/OL]. www. ansys. com. 2009.

[6] RAHANI E K, KUNDU T. Modeling of transient ultrasonic wave propagation using the distributed point source method[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2011, 58(10): 2213-2221.

[7] MARTINS M, CORREIA V, CABRAL J M, et al. Optimization of piezoelectric ultrasound emitter transducers for underwater communications[J]. Sensors and Actuators A: Physical, 2012, 184(9): 141-148.

[8] 刘雪林, 史湘伟, 黄兴洲, 等. 超声波测距声场的仿真研究[J]. 现代电子技术, 2014, 37(5): 101-104.

LIU Xuelin, SHI Xiangwei, HUANG Xingzhou, et al. Simulation research on the sound field of ultrasonic distance measurement[J]. Modern Electronics Technique, 2014, 37(5): 101-104.

[9] LIONETTO F, MONTAGNA F, MAFFEZZOLI A. Ultrasonic transducers for cure monitoring: design, modelling and validation[J]. Measement Science and Technology, 2011, 22(1): 124002.

[10] 张永刚. 声表面波换能器激励的有限元仿真[J]. 声学技术, 2009, 28(5): 678-681.

ZHANG Yonggang. FEM simulation of SAW transducer excitat- ion[J]. Technical Acoustics, 2009, 28(5): 678-681.

[11] 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 3版. 南京: 南京大学出版社, 2012.

DU Gonghuan, ZHU Zhemin, GONG Xiufen. Acoustics founda- tion[M]. 3rd edition. Nanjing: Nanjing University Press, 2012.

[12] ZHENG Dandan, FU Xingyi, YANG Zhibin. Research and rea- lisation of reciprocal electronic circuits for gas ultrasonic flow meter[J]. IET Science Measurement & Technology, 2017, 11(5): 666-672.

Surface vibration and acoustic field measurements of real ultrasonic transducer and its comparison with classic one

SUN Yan-zhao, ZHANG Tao

(School of Electrical and Information Engineering, Tianjin University, Tianjin 300072, China)

The ultrasonic transducers are widely used in acoustic measurements, and their working performance mainly depends on their vibration and acoustic characteristics. In most researches, the transducer is considered as the classic Piston or Gaussian one, but the difference between the real transducer and the classic one is usually ignored. In this paper, the surface vibration and acoustic field of a real made transducer are measured firstly by using laser vibration meter and microphone, and then a finite element scheme is designed to simulate the acoustic fields of the classic and the real transducers. Finally, the differences and similarities between classic and real transducers are analyzed in the three aspects: velocity distribution on radiation surface, pressure along acoustic axis and correlation coefficients. The results show that the velocity distributions on radiation surface are different between these transducers, the acoustic field characteristics of the real transducer are close to the Piston one, but greatly different from the Gaussian one.

ultrasonic transducer; vibration measurement; acoustic measurement; finite element method; acoustic field

TH212 TH213.3

A

1000-3630(2018)-04-0501-06

10.16300/j.cnki.1000-3630.2018.05.016

2017-10-15;

2017-12-18

国家自然科学基金面上项目(61671317)

孙彦招(1984－), 男, 河南平顶山人, 博士研究生, 研究方向为超声换能器和超声流量计。

张涛, E-mail:zt50@tju.edu.cn