一种基于正交非负矩阵分解的多通道线性预测语音去混响方法
2018-11-15何冲王冬霞王旭东蒋茂松
何冲,王冬霞,王旭东,蒋茂松
一种基于正交非负矩阵分解的多通道线性预测语音去混响方法
何冲,王冬霞,王旭东,蒋茂松
(辽宁工业大学电子与信息工程学院,辽宁锦州 121001)
在相对封闭的声学环境中,由于受到混响的影响,麦克风阵列采集到的信号清晰度降低、甚至混淆不清。为了解决这一问题,文章在多通道线性预测(Multi-Channel Linear Prediction, MCLP)语音去混响的基础上,提出了一种改进的多通道线性预测(Multi-Channel Linear Prediction, MCLP)方法即正交非负矩阵线性预测(Orthogonal Non-negative Matrix Factorization Multi-Channel Linear Prediction, ONMFMCLP)方法。该方法利用纯净语音的短时谱域的稀疏性,构建了基于正交的非负矩阵分解(Non-negative Matrix Factorization, NMF)的Kullback-Leibler(KL)问题,通过对矩阵求迹、利用梯度下降法给出迭代规则,进而改进了MCLP中目标信号矩阵的协方差估计。实验结果表明,相对于其他方法,ONMFMCLP方法具有更好的去混响效果。
麦克风阵列;去混响;多通道线性预测;非负矩阵分解
0 引 言
在一些相对封闭的声学环境中使用免提电话、电话会议、助听器、语音控制系统等通信系统时,麦克风采集到的信号往往会受到混响的影响导致语音的清晰度、可懂度等降低,进而影响通信系统的整体功能。因此研究如何去除语音混响即语音去混响也显得愈发重要。
经过多年的发展,人们提出了诸多去混响方法。主要包括基于多通道均衡的去混响方法[1]、基于谱估计和空间滤波器相结合的去混响方法[2]以及基于概率模型的去混响方法[3]。I Kodrasi等[1]提出的多通道均衡去混响方法在理论上可以实现较好的去混响效果,但该方法在实际中会受到房间冲激响应估计准确性的影响;Adam等[2]根据多通道维纳滤波(Multi-channel Wiener Filter, MWF)理论将MWF分解为一个最小方差无失真响应(Minimum Variance Distortionless Response, MVDR)波束形成器和一个单通道维纳滤波器进行去混响处理。该类方法同样也可以实现较好的去混响效果,但需要估计目标信号方向角等参数;而A Jukic等[3]提出的多通道线性预测(Multi-Channel Linear Prediction, MCLP)去混响方法既可以实现较好的去混响效果,又不需要估计任何参数。但该方法会出现目标信号协方差等于零的情况,当情况严重时会出现输出信号失真。
非负矩阵分解(Non-negative Matrix Factorization, NMF)自提出以来便得到学者们的深入研究和广泛的应用[4-5]。根据NMF的分解特性可知,NMF的分解矩阵具有非负的性质,而这种非负性使得这种描述数据的方法具有一定的稀疏性。研究表明,纯净语音的短时傅里叶系数具有一定的稀疏性且大于混响语音信号的短时系数稀疏特性[6-7]。鉴于此,考虑将NMF应用到MCLP去混响中,这样即可以避免目标信号协方差出现等于零的情况,又可以进一步提高语音的去混响性能。
本文介绍了混响的声学模型及MCLP方法,提出了一种正交非负矩阵线性预测(Orthogonal Non-negative Matrix Factorization Multi-Channel Linear Prediction, ONMFMCLP) 方法,最后进行了实验和结果分析。
1 混响信号模型及MCLP方法
在一个单声源的封闭声学环境中,有一个由个全向麦克风组成的均匀线性阵列,则第个麦克风接收到的语音信号的表达式为[3]


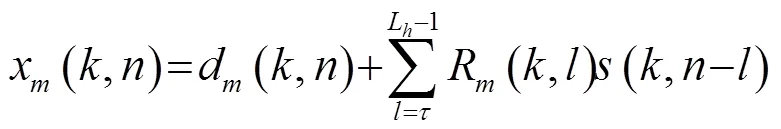
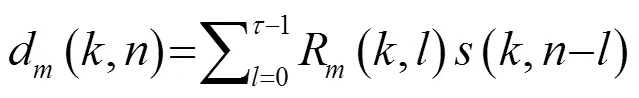
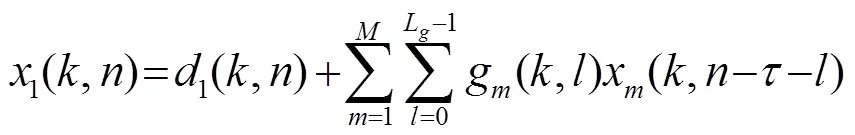
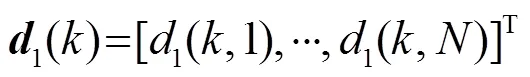
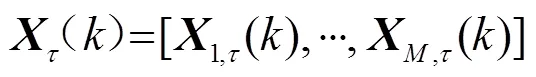
则式(5)的向量表达式为
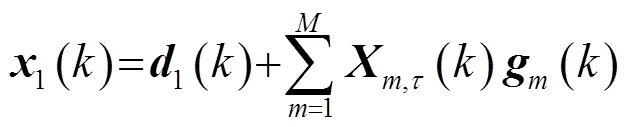




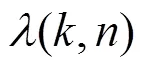
2 基于NMF的协方差估计
在原则上,纯净语音的任何特性都可以加以利用。研究表明,纯净语音的短时傅里叶变换系数具有一定的稀疏性[9],因此可以利用提高输出信号的稀疏性来产生一个近似于纯净语音的信号,根据这一特性可以将其应用到去混响中。
根据式(9)的非负性,首先构造一个矩阵[10]:
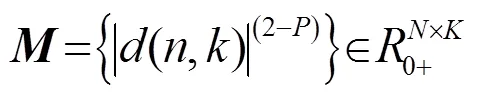
同理,再定义一个非负矩阵也就是协方差矩阵:
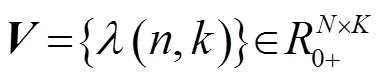
式(11)和式(12)中的和分别表示帧总数和频带总数。根据式(10)中协方差与目标信号的关系,首先用NMF对式(11)进行处理。则其低维表示形式为

式(13)中的表示基矩阵,表示系数矩阵,表示特征维数。则协方差的估计矩阵为

实际使用过程中,为了能够对数据进行有效的数据特征提取并进行有效的表述,需要提高NMF分解的稀疏性。
在已知文献中,NMF直接被应用到语音去混响中,而没有考虑对NMF进行处理,如提高NMF分解的稀疏性。本文将对NMF进行深入的研究以达到进一步提高语音去混响的目的。
以Kullback-Leibler(KL)为代价函数的NMF的系数矩阵不具有正交性即变量之间存在冗余信息。为了去除变量中的冗余信息,可以对其进行正交化处理[11]。这与稀疏性的思想是契合的,也就是说这样能够提高NMF整体的稀疏性。因此,基于式(11)以正交的KL为代价函数的NMF的优化问题可以归纳为
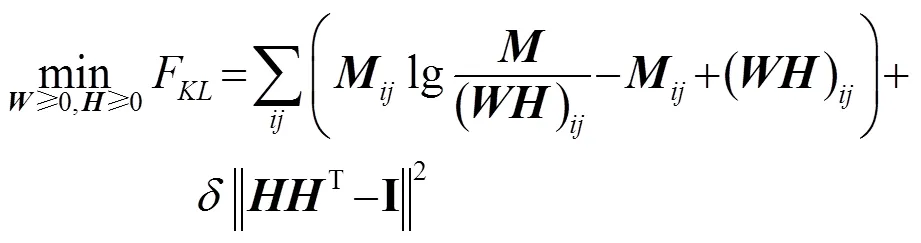


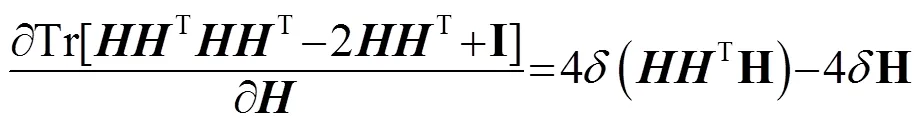

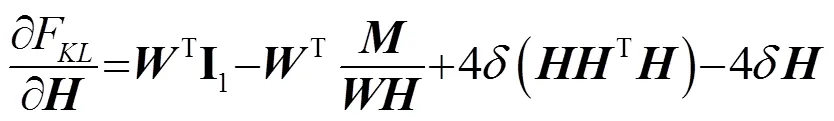
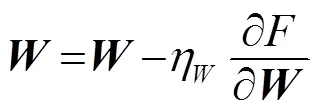


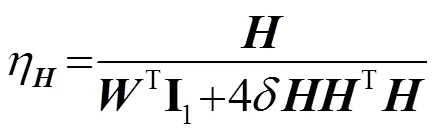
将式(23)、(24)代入到式(21)、(22)中,则



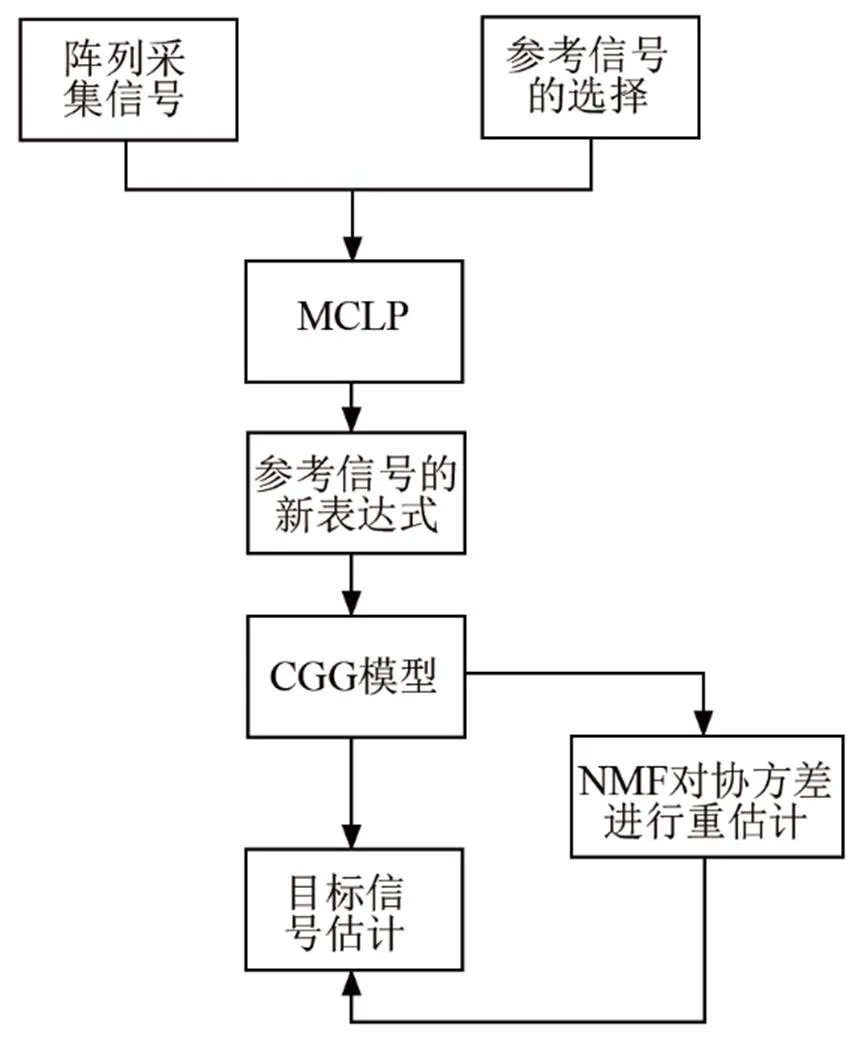
图1 MCLP去混响算法框图
3 仿真实验与结果分析
3.1 仿真环境

为分析本文方法ONMFMCLP的有效性,实验选取了经典三种方法即MCLP[3]、MCLP+TVG+ NMF[10]和IRLS[3]进行了性能比较和分析。
3.2 仿真结果分析
由图2~4可以看出,在各自的混响时间条件下,纯净语音谱的谱分布条理清晰,稀疏性最好。
在轻度混响条件下,混响语音谱的稀疏性仍然比较好;相对于阵列采集信号所对应的混响语音谱,MCLP+TVG+NMF、MCLP、IRLS、NMFMCLP、ONMFMCLP五种方法的去混响效果不明显。
在中度、重度混响条件下,混响语音谱的谱分布布满整个时频域,稀疏性比较差。相对于麦克风阵列采集信号所对应的混响语音谱,MCLP+TVG+NMF、MCLP、IRLS、NMFMCLP、ONMFMCLP五种方法的去混响语音谱的谱分布不再布满整个时频域内,稀疏性得到了明显的提高。
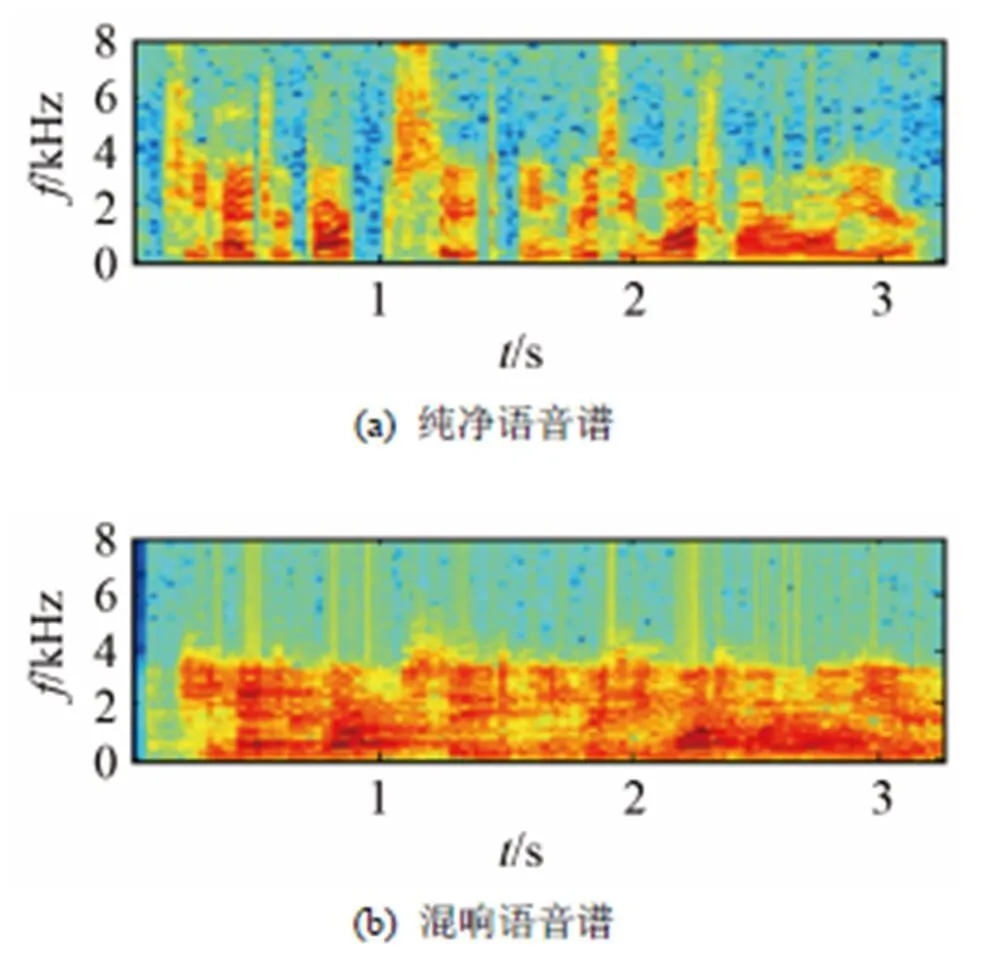

表1是采用主观评测MOS(Mean Opinion Score)法对去混响语音的评价结果。

表 1 主观评价结果
由表1可知,在轻度混响条件下,混响语音及各去混响方法的去混响效果并不是很明显。在中度和重度混响条件下,各去混响方法均起到了一定去混响的效果。
图5、6分别为各混响条件下采用相应客观评价指标即FWSegSNR和PESQ得到的实验结果曲线图。

图5 去混响FWSegSNR曲线图

图6 去混响PESQ曲线图
从图5、6中可以看出,在各种混响条件下,相对于混响语音,无论是去混响参数FWSegSNR或PESQ,MCLP+TVG+NMF、MCLP、IRLS、NMFMCLP、ONMFMCLP五种去混响方法的评估参数都得到了显著的提高。
在轻度混响条件下,MCLP、IRLS、NMFMCLP、ONMFMCLP四种方法的FWSegSNR的提高明显优于MCLP+TVG+NMF方法。而MCLP+TVG+NMF方法的PESQ提高优于其它几种方法。
在中度、重度混响条件下,NMFMCLP,ONMFMCLP两种方法的性能参数明显高于MCLP+TVG+NMF、MCLP、IRLS三种方法且MCLP+TVG+NMF方法去混响性能最差;综合以上FWSegSNR和PESQ两个性能参数,ONMFMCLP去混响方法几乎等价于NMFMCLP。
各种语音去混响方法的程序运行时间柱状图如图7所示。
由图7可知,MCLP、IRLS两种方法的程序运行时间一致且最短;NMFMCLP方法的运行时间次之;MCLP+TVG+NMF、ONMFMCLP方法的运行时间最长。故改进方法即NMFMCLP/ONMFMCLP方法虽然进一步提高了语音的去混响性能,但是其计算复杂度有明显增加。

图7 各去混响方法的运行时间柱状图
4 结论
本文充分考虑了语音的时频域稀疏性及其NMF的特性,对阵列接收目标信号的协方差进行了改进,即通过构建正交KL为代价函数的NMF优化问题,利用梯度下降法对其进行推导,得到了协方差矩阵的估计值,以达到进一步提高语音的去混响性能。实验结果表明,相对于其他去混响方法,在不需要估计混响时间等参数的前提下,NMFMCLP/ONMFMCLP去混响方法在一定程度上改善了语音去混响性能。但是该方法也有一定的不足之处,例如计算复杂度有明显增加;另外,NMF的初始化具有随机性。
[1] KODRASI I, JUKIC A, DOCLO S. Robust sparsity promoting acoustic multi-channel equalization for speech dereverberation[C]//IEEE International Conference on Acoustics, 2016: 166-170.
[2] KUKLASINSKI A, DOCLO S. Maximum likelihood PSD estimation for speech enhancement in reverberation and noise[J]. IEEE/ACM Transactions on Audio Speech & Language Processing, 2016, 24 (9): 1595-1608.
[3] JUKIC A, WATERSCHOOT T V, GERKMANN T, et al. Multi channel linear prediction-based speech dereverberation with sparse priors[J]. IEEE/ACM Transactions on Audio Speech & Language Processing, 2015, 23 (9):1509-1520.
[4] MOHAMMADIHA N, SMARAGDIS P, LEIJON A. Supervised and unsupervised speech enhancement using nonnegative matrix factorization[J]. IEEE Transactions on Audio Speech and Language Processing, 2013, 21(10): 2140-2151.
[5] AKARSH K A, SELVI R S. Speech enhancement using non-negative matrix factorization and enhanced NMF[C]//International Conference on Circuit, 2015: 1-7.
[6] MOHAMMADIHA N, DOCLO S. Speech dereverberation using non-negative convolutive transfer function and spectro-temporal modeling[J]. IEEE Transactions on Audio Speech & Language Processing, 2016, 24(2): 276-289.
[7] MOHAMMADIHA N, SMARAGDIS P, DOCLO S. Joint acoustic and spectral modeling for speech dereverberation using non-negative representations[C]//IEEE International Conference on Acoustics, 2015, 8(4): 4410-4414.
[8] BRADLEY J S, SATO H, PICARD M. On the importance of early reflections for speech in rooms[J]. J. Acoust. Soc. Am., 2003, 113(6): 3233-3244.
[9] TASHEV I, ACERO A. Statistical modeling of the speech signal[C]//International Workshop on Acoustic Echo & Noise Control Tel Aviv Israel, 2010.
[10] JUKIC A, MOHAMMADIHA N, WATERSCHOOT T V. Multi-channel linear prediction-based on speech dereverberation with low-rank power spectrogram approximation[C]//IEEE International Conference on Acoustics, Speech and Signal Processing, IEEE, 2015, 23(9): 96-100.
[11] 崔建. β散度的非负矩阵分解在基因聚类中的应用研究[D]. 重庆: 重庆大学, 2015.
CUI Jian. The application of non negative matrix factorization of beta divergence in gene clustering[D]. Chongqing: Chongqing University, 2015.
[12] FÉVOTTE C, BERTIN N, DURRIEU J L. Nonnegative matrix factorization with the Itakura-Saito divergence: with application to music analysis[J]. Neural Computation, 2009, 21(3): 793.
[13] GAROFOLO J S, LAMEL L, FISHER W, et al. TIMIT Acoustic-Phonetic Continuous Speech Corpus[J]. Journal of the Acoustical Society of Amercia, 1993, 88(88): 210-221.
[14] HADAD E, HEESE F, VARY P, et al. Multichannel audio database in various acoustic environments[C]//International Workshop on Acoustic Echo and Noise Control, Antibes, France, 2014: 313-317.
[15] HU Y, LOIZOU P C. Evaluation of objective quality measures for speech enhancement[J]. Transactions on Audio Speech and Language Processing, 2008, 16(1): 229-238.
Speech dereverbration based on MCLP using orthogonal NMF
HE Chong, WANG Dong-xia, WANG Xu-dong, JIANG Mao-song
(School of Electronic and Information Engineering, Liaoning University of Technology, Jinzhou 121001, Liaoning, China)
In a relatively closed acoustic environment, the speech signals can be severely affected by reverberation, which degrades the intelligibility of speech and even results in confusion. In order to solve this problem, this paper presents a new dereverbration algorithm called ONMFMCLP based on the well-known multi-channel linear prediction (MCLP). This algorithm utilizes the sparse nature of clean speech in the short time spectrum domain to construct the KL optimization problem based on the orthogonal NMF. The iterative rules are given through solving the matrix trace and utilizing the gradient descent method, thereby improving the signal covariance matrix in the MCLP algorithm. Experimental results show that the ONMFMCLP algorithm can achieve a better dereverberation performance compared with other algorithms.
microphone array; dereverbration; Multi-Channel Linear Prediction (MCLP); Non-negative Matrix Factorization (NMF)
TN912.35
A
1000-3630(2018)-05-0468-07
10.16300/j.cnki.1000-3630.2018.05.011
2017-06-29;
2017-08-13
辽宁省自然科学基金(201302022)资助项目。
何冲(1990-), 男, 河南南阳人, 硕士研究生, 研究方向为现代信号处理与多媒体技术。
王冬霞, E-mail: dxwang_lg@126.com
