基于大涡模拟和Lighthill声类比的孔腔流动发声特性研究

胡明慧，占必武



基于大涡模拟和Lighthill声类比的孔腔流动发声特性研究

胡明慧，占必武

(华东理工大学承压系统与安全教育部重点实验室，上海 200237)

孔腔流动发声是气动声学研究领域重要的课题，基于大涡模拟和Lighthill声类比方法，探讨了气体在孔腔流动的流激噪声的发声特性。模拟结果表明，孔腔边界层出口剪切涡、边棱处涡街和腔体内反馈涡的运动诱导了孔腔发声，具有明显的偶极子特性，在高频段腔体内激发了声学驻波模态。通过模拟与实验对比分析了不同流量下噪声量级以及频谱分布规律，研究结果表明：24 kHz以下的声频谱会表现出波峰小范围迁移；24 kHz以上频率对应的声压级随流量增大而增大；腔体长度和特征频率近似满足Strouher公式，即声频特征频率随腔体长度的增大而减小。上述研究结果为下一步设计在线监测安全阀泄漏的报警超声波发声器提供了理论依据。

孔腔；大涡模拟；Lighthill声类比；涡声；声频特性

0 引言

孔腔是一种复杂的空腔结构，在很小流速驱动下就能发出超声波气动噪声。当气流流过空腔时，由于腔内外存在较大的速度梯度，使得空腔外剪切层与腔内流动发生相互作用产生周期性剧烈脉动，从而诱发强烈的气动噪声[1-2]。在气动噪声混合方法计算方面，国内外众多学者采用大涡模拟(Large Eddy Simulation, LES)和Lighthill声类比方法对腔体的低马赫数流致噪声进行了预测[3-5]。肖友刚等[6]采用大涡模拟和Lighthill声类比的方法成功预测了高速列车车头曲面的气动噪声。杨党国等[7]利用FW-H (Ffowcs Williams-Hawkings)积分方程探讨了空腔自激振荡发声机理。

目前，国内外学者对气动噪声的研究主要集中在中低频，对频率在20 kHz以上的高频气动噪声的研究文献几乎没有。在实际工业应用中，如何利用低马赫数下孔腔流动能激发强超声波噪声的特性，为监测核电蒸汽安全阀泄漏设计在线报警超声波发声器，通过检测超声波来判断安全阀是否发生内泄漏，对保证我国核电设备的安全运行具有重大意义。本文以LES和Lighthill声类比理论为基础，以孔腔流动发声为研究对象，通过模拟和实验对比，分析了低马赫数下孔腔流激噪声的发声特性，探讨了孔腔的腔体入口流量对噪声频谱特性的影响规律，为下一步设计在线监测安全阀泄漏的报警超声波发声器提供参考和借鉴。

1 基本理论

1.1 大涡模拟方法

考虑到现有计算机资源较难满足直接模拟法(Direct Numerical Simulation, DNS)的求解要求，雷诺平均N-S方程法(Reynolds Average Navier-Stokes, RANS) 只提供湍流脉动的时均信息，不适合噪声预测，故本文采用LES方法对瞬态流场进行数值计算。LES 方法把湍流中的含能区大涡和耗散区小涡分开处理，大尺度涡结构用 N-S 方程直接求解，而小尺度涡通过亚格子模型与大尺度涡建立关联[8]。对非定常的N-S方程进行滤波，得到大涡模拟的控制方程，滤波过程有效地过滤掉了那些尺度小于滤波宽度(或网格尺度)的小涡[9]。

滤波后的大涡模拟方程为

1.2 Lighthill声类比方法

声类比理论最初由Lighthill[10-11]提出，后经Curle，Ffowcs-Williams和Hawkings推广。本文基于Lighthill声类比，既考虑偶极子噪声，也考虑四极子噪声。将大涡模拟瞬态流场计算的压力脉动结果转化为声学计算的声源项，运用有限元/无限元计算方法，对可压缩流体声学特性进行计算[12]。

由于方程的非线性和流动与声场的耦合性使方程不易求解，将声场分为近场和远场，近场为声源区，远场为辐射区，假定辐射区的流动对声场没有影响，其形式为:

2 孔腔流激噪声仿真

2.1 计算模型及网格

孔腔实物如图1所示，利用CATIA软件建立1∶1三维模型。为了将模拟结果和实验进行对比，模拟参数选取：孔腔声频测试距离为130 mm、流量为2.5 L·min-1(折合流速为5.5 m·s-1)。经过多次试算，外部流体域选取22 mm´16 mm´14 mm的矩形域，保证在计算域内部得到充分发展的湍流流场。

图1 孔腔结构

为了准确获取孔腔流场的信息，把孔腔流体域切分进口左端(Pipe_Left), 中间端(Pipe_Mid), 右端(Pipe_Right), 出口端(Pipe_Out), 外部空气域(Opening)这五个部分，在ICEM软件中对其进行网格划分，如图2(a)所示。为了满足LES对近壁面的要求，对每部分网格做近壁面加密处理。孔腔整体网格如图2(b)所示，网格数量为340万，网格质量在0.35以上。

图2 孔腔网格划分

2.2 流场特性模拟

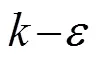
表1 边界条件设置

稳态计算完成后，开始进行LES计算。选择WALE亚格子模型，压力基耦合隐式求解器，时间离散选用二阶隐式，动量离散方法设置成中心差分格式，时间步长设置为5×10-6s。待残差和监测的压力出现周期性波动时，说明流场已经达到动态稳定状态。此时继续进行2 000步LES计算，同时输出每一步的压力、密度和速度数据，为声场计算提供“声源”结果。

图3为流场达到稳定后任取某时刻的速度和等值面图。从图3中可以看出，气流通过孔腔后，由于空腔内外较大的速度梯度，会在区域1处形成不稳定的剪切层(内含涡结构)，剪切涡在孔腔出口受到剪切力的作用而产生涡的脱落，脱落的涡一部分在孔腔后部空腔内聚集，一部分顺着孔腔边棱向外传播。在空腔内部聚集的涡撞击到空腔底部反弹，返回与区域1处的涡发生干涉，进而形成反馈回路。

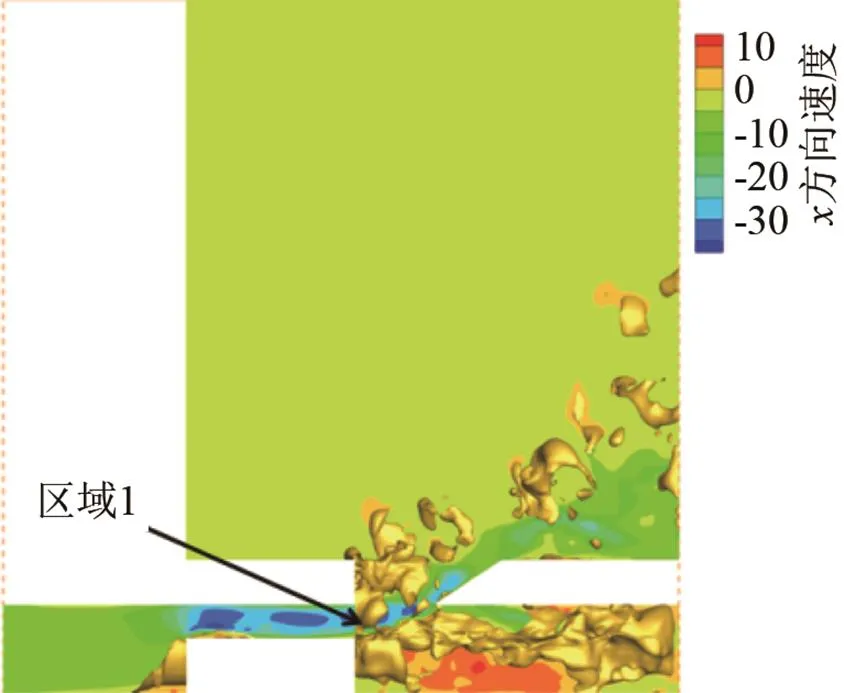
图3 截面速度和等值面图

孔腔稳态时均流场速度矢量图如图4所示，由于孔腔挡块的截流作用使得边界层内速度急剧增加且气流在边界层出口处形成射流，射流出来的气流撞击在边棱并从边棱两侧流动。进入腔体的气流刚开始向腔体下游流动并在孔腔体内形成大旋涡，与下游底部发生碰撞后改变流动方向，朝着上游流动，最终在射流出口处发生耦合。

2.3 声场特性模拟

孔腔声场模型分为声源域、声传播域、无限元域三部分，使用四面体网格划分方法，每个波长8个网格，最小网格尺寸为0.8 mm，孔腔声场模型和网格如图5所示。将整个孔腔大涡模拟流场数据插值声源域网格从而得到模拟声源，利用Lighthill声类比方法计算孔腔声源在有限空间内的声传播辐射情况，为了保证计算精度并减小计算量，本文选取椭球体包裹声源域。椭球体的表面为无限元域，用来模拟无反射边界条件。同时为了和实验结果作对比，在孔腔出口正上方130 mm处设置声压测量点。声场最大计算频率为40 kHz，最小计算频率为100 Hz。

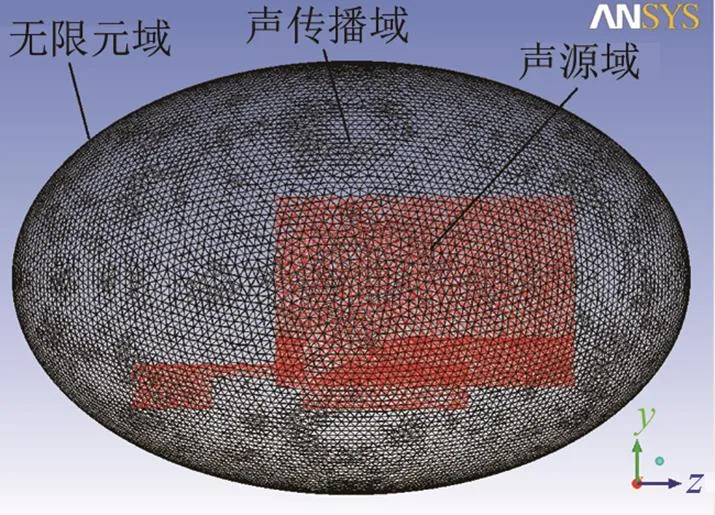
图5 孔腔声场模型和网格

孔腔整体声压级分布如图6所示。由图6可知，频率增大时，声场的最大声压级逐渐减小，这和孔腔声源强度随频率变化的规律一致。当频率为5 000 Hz时，最大声压级为113 dB，当频率为35 000 Hz时，最大声压级只有75.8 dB。当频率相对较低为5 000 Hz和15 000 Hz时，孔腔声场声压级较大的地方主要集中在孔腔边界层、腔体和孔腔出口上方区域，边界层和腔体内声压级基本趋于一致。由于噪声主要是从孔腔出口向外传播，频率为5 000 Hz时，明显可见出口气流冲击静止空气而带来的声压迅速耗散。当频率到达超声段，为25 000 Hz和35 000 Hz时，最大的特点是在孔腔腔体内激发了管道声学驻波模态，且边界层内声压级也变得不再均匀。孔腔具有边棱结构，包含边棱音成分，而边棱音是偶极子发声占主导[13-15]。孔腔声场均有类似“梨形”的声压脉动。

图6 孔腔整体声压级分布

3 孔腔流激噪声声频测试实验

3.1 实验系统

本实验在某全消声室内完成。测试对象为国外进口的铜制孔腔，其腔体长度可调。气源由带减压阀的2个10 MPa压缩空气瓶提供，用量程为10 L·min-1的质量流量计计量孔腔入口的流量。声频采集设备包括：B&K 4135传声器(频率响应4～100 kHz、动态范围39～164 dB)、 B&K 2633前置放大器、NI 4497采集设备(可将采样频率设置为200 kHz)等。由奈奎斯特采样定理可知，此测试设备采集到的最大声频为100 kHz。实验布置如图7所示。

将孔腔可调部分螺纹旋至1/2处，其出口离传声器距离为130 mm。本实验测得孔腔入口流量从0.5L·min-1到5.5L·min-1共11组数据。

图7 实验装置图

3.2 实验结果

流量是影响孔腔声频特性的最重要的参数，为了分析一阶特征频率波峰随流量变化的迁移规律，实验测量了多种流量下声频率特性曲线，如图8所示。由图8可知，孔腔在24 kHz以下频段会表现出波峰小范围迁移，流量从1 L·min-1到2 L·min-1，一阶特征频率基本呈线性增长，直到3 174 Hz；但是当流量增加到2.5 L·min-1，一阶特征频率跳到7 813 Hz，发生了很大的阶跃，流量到3 L·min-1时，一阶特征频率继续小范围增加到8 057 Hz；当流量增加到3.5 L·min-1时，一阶特征频率骤降到5 371 Hz，流量从3.5 L·min-1到5.5 L·min-1，一阶特征频率又呈线性增加，且和流量从1 L·min-1到2 L·min-1的增加斜率几乎一样。对于24 kHz以上的超声频段，孔腔声频谱的趋势具有高度的一致性，各离散频率对应的声压级随着流量的增大而增大，特征波峰固定不动，表现出超声锁频特性。

为了验证模拟与实验方法的准确性，本文对2.5 L·min-1流量下的实验和模拟声频特性曲线进行对比分析，如图9所示。试验和模拟的整体声压级都呈衰减趋势，都在一阶特征频率处有最大声压级(一阶特征频率的实验值为7 813 Hz，模拟计算值为7 500 Hz)。在0～20 kHz频段，试验和模拟的声频谱特性一致，高次谐波都能体现出来。在20～40 kHz的超声频段，两者的频谱变化趋势基本相同，但是数值模拟计算的离散高频对应的声压级整体稍偏小，这是高频计算误差所致。因为计算频率越高，要求网格和声学模型的数值误差越小，需要更合理、更小的网格和高精度的湍流模型和声学模型。

图9 孔腔声频率特性实验结果和模拟结果对比

上述分析表明，实验结果和模拟结果的总体趋势十分吻合，验证了LES与Lighthill声类比相结合的方法分析孔腔声频特征的准确性。

4 结论

本文通过实验和模拟的方法探究了孔腔结构的流动的发声特性，主要得出了以下结论：

(1) 利用LES/Lighthill声类比混合方法对孔腔流场和声场进行计算，推断出孔腔边界层出口的剪切涡、边棱处形成的涡街和腔体内反馈涡的运动诱导了声的产生。

(2) 通过实验验证了在低流速、低马赫数气体流动下孔腔能够产生高频超声特性。其中，24 kHz以下声频会表现出波峰小范围迁移；对于 24 kHz以上的超声频段，孔腔声频谱的趋势具有高度的一致性，表现出超声锁频特性。

(3) 为了验证模拟与实验方法的准确性，本文对2.5 L·min-1流量下的实验结果和模拟声频特性曲线进行了对比分析，结果表明，实验结果和模拟结果总体趋势十分吻合。

[1] POWELL A. Theory of vortex sound[J]. J Acoust. Soc. Am., 1964, 36(1): 177-195.

[2] NAKIBOGLU G, HIRSCHBERG A. Aeroacoustic power generated by multiple compact axisymmetric cavities Effect of hydrodynamic interference on the sound production[J]. Physics of fluids, 2012, 24(6): 529-549.

[3] HOWE M S. Mechanism of sound generation by low Mach number flow over a wall cavity[J]. Journal of Sound and Vibration, 2004, 273(1-2): 103-123.

[4] ZHANG Y O, ZHANG T, OUYANG H, et al. Flow-induced noise analysis for 3D trash rack based on LES/Lighthill hybrid method[J]. Applied Acoustics, 2014, 79(1): 141-152.

[5] KALTENBACHER M, ESCOBAR M, BECKER S. Numerical simulation of flow-induced noise using LES/SAS and Lighthill's acoustic analogy[J]. International Journal for Numerical Methods in Fluids, 2010, 63(9): 1103-1122.

[6] 肖友钢, 康志成. 高速列车车头曲面气动噪声的数值预测[J]. 中南大学学报(自然科学版), 2008, 39(6): 1267-1272.

XIAO Yougang, KANG Zhicheng. Numerical prediction of aerodynamic noise radiated from high speed train head surface[J]. J. Cent. South Univ. (Science and Technology), 2008, 39(6): 1267-1272.

[7] 杨党国, 李建强, 梁锦敏. 基于CFD和气动声学理论的空腔自激振荡发声机理[J]. 空气动力学学报, 2010, 28(6): 724-730.

YANG Dangguo, LI Jianqiang, LIANG Jinmin. Sound generation induced by self-sustained oscillations inside cavities based on CFD and aeroacoustic theory[J]. ACTC Aerodynamica Sinica, 2010, 28(6): 724-730.

[8] WAGNER C, HUTTL T, SAGAUT P. Large-eddy simulation for acoustics[M]. Cambridge University Press, 2007.

[9] GRIGORIADIS D G E, BARTZIS J G, GOULAS A. LES of the flow past a rectangular cylinder using the immersed boundary concept[J]. International Journal for Numerical Methods in Fluids, 2003, 41(6): 615-632.

[10] LIGHTHILL M J. On sound generated aerodynamically: Part I: general theory[J]. Proceedings of the Royal society of London, 1952, 211(1107): 564-587.

[11] LIGHTHILL M J. On sound generated aerodynamically: Part II: turbulence as a source of sound[J]. Proceedings of the Royal Society of London, 1954, 222(1148): 1-32.

[12] 张咏鸥, 张涛, 刘继明, 等. 基于Lighthill声类比的流激噪声三维计算及验证[J]. 舰船科学技术, 2014, 36(9): 55-59.

ZHANG Yong’ou, ZHANG Tao, LIU Jiming, et al. Three dimensional simulation and validation of the flow-induced noise based on Lighthill’s acoustic analogy theory[J]. Ship Science and Technology, 2014, 36(9): 55-59.

[13] POWELL A. On the edgetone[J]. J Acoust. Soc. Am., 1961, 33(4): 395-409.

[14] SAMUEL A E. The mechanism of sound production in organ pipes and cavity resonators[J]. J Acoust. Soc. Jpn. (E), 1992, 13(1): 11-23.

[15] SHIGERU Y, HIROMI T, YUMIKO S. Experimental examination of vortex-sound generation in an organ pipe: a proposal of jet vortex-layer formation model[J]. Journal of Sound and Vibration, 2012, 331(11): 2558-2577.

Research on the characteristics of sound generated by flow inside cavity based on LES and Lighthill acoustic analogy method

HU Ming-hui, ZHAN Bi-wu

(Key Laboratory of Pressure Systems and Safety, East China University of Science and Technology, 200237, Shanghai, China)

Cavity flow is an important issue in the field of aeroacoustics. By using LES (large eddy simulation) and Lighthill acoustic analogy method, the characteristicsof sound generated by flow inside cavity have been discussed. Simulation results show that the sound generated by shear vortex, edge vortex and feedback vortex has obvious dipole characteristics. Acoustic standing wave is excited at high frequency. By simulation and experiment, the magnitude of noise and the distribution of spectrum under different flow rates are analyzed. The results show that the acoustic frequency locking characteristic could happen under different paraments of cavity length, diameter and baffle length, and that the frequency spectrum has a small range migration of the peak below 24 kHz and the sound pressure level increases with the flow rate above 24 kHz. The relation between cavity length and characteristic frequency is approximately satisfied with Strouher’s formula, and the characteristic frequency decreases with increasing the length of cavity. The research provides a theoretical basis for the design of the ultrasonic safety valve leakage alarm system for on-line monitoring.

cavity; large eddy simulation(LES); Lighthill acoustic analogy; vortex sound; acoustic frequency characteristics

TB533+.3

A

1000-3630(2018)-05-0412-06

10.16300/j.cnki.1000-3630.2018.05.002

2018-03-23;

2018-05-10

国家自然科学基金(51775188)资助项目。

胡明慧(1974－), 女, 江西南昌人, 副教授, 研究方向为泄漏在线声学检测。

胡明慧,E-mail: agile_hu@ecust.edu.cn