高中物理极值问题的物理求解方法

竺 斌

(浙江省湖州中学，浙江 湖州 313000)

物理极值问题是求解某个物理量在某个过程中出现的极大值或者极小值的问题.这对某个物理量的研究具有非常重要的作用,特别对某些实际问题具有极其重要的价值.一般的处理方法是用数学方法来求解,但有时写出的函数关系非常复杂,很难求出它的极值,或者求解过程非常繁琐,或者求解过程的数学运算量非常大.所以有些问题,我们可以考虑是否通过对物理过程的分析,从物理角度思考达到极值所满足的物理条件,根据这一条件进行求解,可能会带来意想不到的惊喜.另外,有些物理量的函数关系不能直接写出,这类问题的解答可能会有些技巧,比如利用类比的方法,将这一问题与我们熟悉的问题进行类比,问题也就迎刃而解了.下面介绍的利用光学中的费马原理来求解一些运动学的问题就是典型的例子.

1 分析物理过程,找出达到极值所满足的物理条件

(1) 计算运动过程中的最高点和最低点,这些位置,运动物体的速度一定是水平的,竖直分速度为0,否则就不可能为最高点或最低点.抓住这特点进行求解问题就迎刃而解了.

图1

例1.(2018年4月浙江省选考科目考试物理试题的选择题第13题)如图1所示,一根绳的两端分别固定在两座猴山的A、B处,A、B两点水平距离为16 m,竖直距离为2 m,A、B间绳长为20 m.质量为10 kg的猴子抓住套在绳子上的滑环从A处滑到B处.以A点所在水平面为参考平面,猴子在滑行过程中重力势能最小值约为(绳处于拉直状态)

(A) -1.2×103J. (B) -7.5×102J.

(C) -6.0×102J (D) -2.0×102J.

图2

本题考查了重力势能的最小值.重力势能最小,也就是猴子沿绳子下滑到最低点,这是一题求高度最低的极值问题.一般的数学解法,猴子的运动轨迹是以A、B为焦点的椭圆,建立以AB所在直线为x轴,AB中点为坐标原点,写出椭圆方程,如图2所示.最低点位置是椭圆的切线水平,即斜率为-0.125的点(有两个Q、Q′),其中一个Q就是高度最低的点.这样的计算肯定比较繁琐,而且要用到求导.

图3

如果用物理方法可以方便的确定最低点的位置.猴子运动到最低点时,速度方向一定是水平的.如图3所示,猴子运动到最低点时滑轮的位置记为Q点,过Q点做水平线MN,过Q点做竖直线QP,即MN⊥QP.猴子运动轨迹是椭圆,速度沿切线方向(水平MN方向),根据椭圆的光学性质,法线QP一定平分∠BQA,即∠BQP=∠PQA.接下来根据平面几何的知识很容易得到QA的高度为7 m.

(2) 物体做变加速运动的过程,若加速度先减小后反向增加,速度先增加后减小.那么速度最大的时刻也即加速度为0的时刻或者合力为0的时刻.

例2.一质量为m的小环A套在光滑的水平固定杆中,并用长为l的细绳与质量也为m的小球B连接,先将绳拉至水平方向,然后静止释放.当绳与水平杆之间的夹角θ为多大时,小球B的速度最大,并求出此最大速度.

图4

解析:小球B对地速度为vB,相对环A的速度为vBA,小环A的速度为vA.如图4所示.它们之间的关系:vBx=vBAsinθ-vA，

vBy=vBAcosθ.

当小球摆至绳子与水平方向的夹角为θ时,根据机械能守恒可得

系统水平方向动量守恒可得:

mvA=mvBx

由以上几式可解得

设绳子的拉力为F,小环的加速度为a,则有Fcosθ=ma.

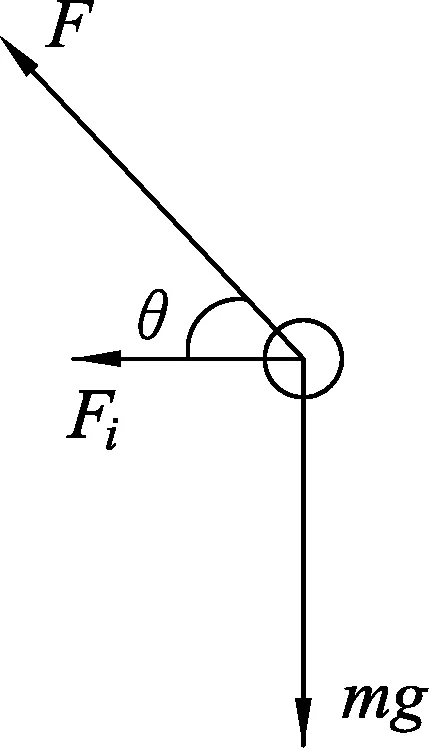
图5

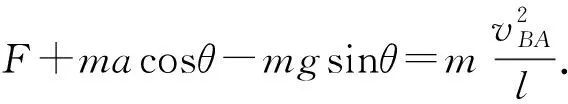
要使小球速度最大,那么小球沿对地速度vB方向的合力为0,有

mgcosα=Fsin(θ-α)

可得3cos4θ+8cos2θ-3=0.

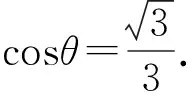
2 类比方法求极值

类比是物理学的重要方法之一,对物理学的发展起了积极的促进作用.有些运动学的极值问题可以类比于光学中的折射定律(或者费马原理),应用折射定律解决非常的简捷.比如“胡不归”问题和均匀重力场中最快下降路线.下面分别来探讨这两个问题.

2.1 “胡不归”问题

图6

古老的“胡不归”传说,说的是:从前有一个身在A地当学徒的小伙子,当他得悉在家乡B地的年老父亲病危的消息后,便立即向掌柜告了假,借了些钱,启程赶路,由于思念心切,他挑选了全是沙砾地带的直线路径AB(如图6所示),他认为走近路必定最省时,因此,他放弃了沿驿道AC先走一程的想法.当他气喘吁吁地来到父亲跟前时,老人刚刚咽了气,小伙子不觉失声痛哭.邻舍闻声前来劝慰,有人告诉小伙子,老人在弥留之际,还不断喃喃地叨念“胡不归?胡不归?……”

例3.现给“胡不归”问题附以数据,B地到驿道的直线距离为12 km,AB两地的直线距离为20 km.沿沙砾地带步行的速度为1 m/s,在驿道骑马的速度为10 m/s.那么小伙子怎样的走法从A地到B地的时间最短.

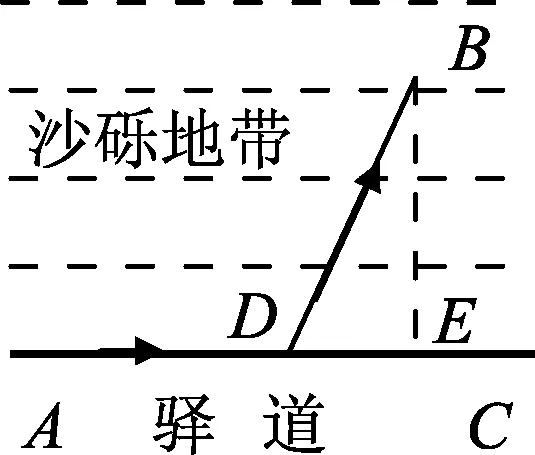
图7

解析:如果将此问题建立数学模型,转化为数学的求极值问题可以求解,但是求解过程复杂,要用到导数求极值的方法.现在将此问题与光的折射联系起来,用折射定律求解,要方便得多.我们设想从A点发出的一束光(代替小伙子)先与两媒质(驿道跟沙砾地带)界面AC(即驿道)成一很小的角度入射到D点,此时光速为v1,然后折射入第二种媒质(沙砾地带)到达B点,此过程中光速为v2,如图7所示.假定此光束沿ADB路线传播是符合折射定律的路径,根据费马原理:光线在两点间的实际路径是使所需的传播时间为极值的路径.光的折射定律就是费马原理的一个推论,光从一种介质进入另一种介质走的路径是所需时间最短的路径.所以小伙子走ADB路线所用时间最短.

根据折射定律及折射率与速度的关系可得,

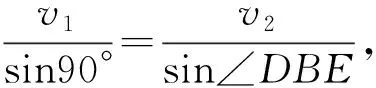
所以小伙子先沿驿道骑马行走约14.79 km至D点,然后进入沙砾地带沿DB方向步行至B地,所用时间最短.

2.2 重力场中最快下降路线.

例4.在某一竖直面上有O、P两点,这两点的水平距离为a,竖直距离为b.试找出一条从O点到P点的光滑曲线轨道,使得质点从O点静止出发无摩擦的沿此轨道滑到P点所需的时间最短.

解析: 光的折射定律为n1sinθ1=n2sinθ2，

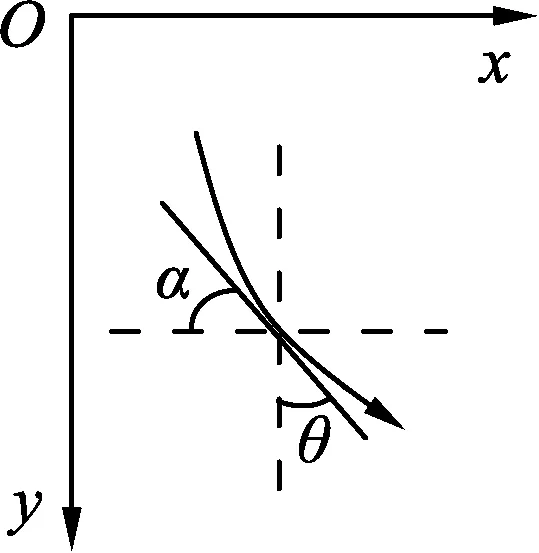
图8

图9

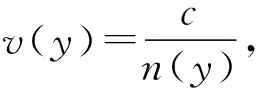
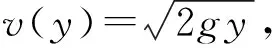
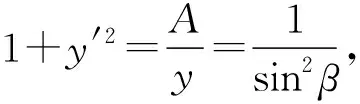
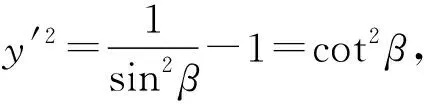
由以上两式可得dx=2Asin2β·dβ.

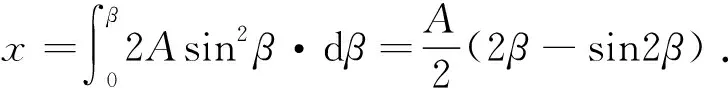
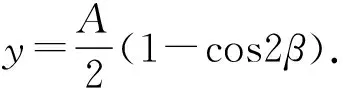
所以得到质点在重力场中的最快下降路线的参数表达式为

其中参数A可由P点的坐标a和b通过下面两式确定,

由此可见,最快下降路线是一条摆线.

综上所述,用物理方法求解极值问题,必须有敏锐的物理洞察力.根据题意,找出取到极值满足的物理条件,或者根据已有的一些物理规律,巧妙的运用类比方法,找到求解极值问题的关键,这是用物理方法求解极值问题的核心,不能盲目地将物理问题纯数学化.研究物理极值的物理解法,不仅可以增强学生对物理概念、物理过程以及物理规律的认识和理解,而且也可以省去复杂繁琐的数学计算.