考虑热场的重型燃气轮机组合转子盘间接触应力分析

卓明,杨利花,夏凯,虞烈

(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学机械结构强度与振动国家重点实验室,710049,西安;3.西安交通大学陕西省先进飞行器服役环境与控制重点实验室,710049,西安)

重型燃气轮机组合转子服役于高温严酷环境,冷态装配时接触良好的各盘间接触界面,在温度场作用下,由于拉杆、轮盘间的径向、轴向热膨胀不一致,其接触应力分布会发生变化,从而增加接触分离的风险,影响组合转子的结构完整性及动力学特性,因此有必要研究组合转子各工况温度场对各盘间接触应力分布的影响,为冷态装配时拉杆预紧力的裕度设计提供参考。

国内外关于组合转子盘间接触应力分布的研究主要集中在冷态载荷作用情况。Richardson用三维有限元法研究了端面齿接触,并用光弹性测试结果进行了对比[1],结果表明限元法是研究端面齿接触的一种可靠计算方法,且其精度依赖于接触区域精细的网格划分及接触面间的黏-滑行为处理。李辉光研究了预紧力、离心力、扭矩及横向载荷等不同冷态载荷对各盘间最大接触应力的影响[2]。王为民给出了重型燃气轮机组合转子盘间接触界面的设计准则[3]。李浦等提出了用冲压模型来计算端面齿连接转子预紧和传扭时的齿面径向平均接触应力[4]。卢明剑研究了端面齿在预紧-升速-传扭过程中的应力应变规律,同时分析了端面齿的最大接触应力及强度对其几何结构参数的敏感性[5]。赵仕志等模拟了燃气轮机压气机第3级轮盘与拉杆螺母间接触面在预紧过程中的接触应力分布[6]。

涉及组合转子温度场的研究主要集中在等效应力分布及低周疲劳寿命计算方面,而温度场对组合转子盘间接触应力分布的影响研究则涉及较少。Endres假设轮盘之间无相互作用,讨论了重型燃气轮机转子的不同内部结构设计在热应力作用下的结构强度及低周疲劳表现[7]。欧文豪等用连续燃气轮机转子模型研究了冷启动及热启运过程中的温度场及应力场变化,并评估了两种启动工况下的寿命损耗率[8]。李朝阳等采用循环对称模型,对燃气轮机透平第1级涡轮盘启动过程中的温度及应力场进行了计算[9]。石清鑫等将透平转子轮盘间的接触视为绑定接触,研究了透平转子的稳态温度场及应力场分布[10]。Das对两种不同结构的F级拉杆转子进行三维稳态及瞬态热-结构耦合分析,预测了转子拉杆及轮盘的高应力区域[11]。Janssen等给出了中心拉杆在包括启机,稳态和停机的一个正常工作循环中的应力变化,中心拉杆的等效应力在启动过程中变化最大[12]。Yuan等研究了稳态温度场对透平转子端齿接触应力分布的影响[13]。

本文建立了重型燃气轮机组合转子的1/12循环对称有限元模型,针对预紧、升速等冷态工况及包含稳态、启停和盘车等热工况的一个典型工作循环,分别进行了结构分析和热-结构耦合分析,得到了预紧力、离心力、稳态和瞬态热载荷作用下各盘间接触应力的分布规律。

1 计算方法

1.1 有限元模型

本文重型燃气轮机组合转子的几何结构及有限元模型如图1所示。组合转子由两段过渡段分别连接压气机段和透平段组成。压气机段和透平段分别由17级轮盘、4级轮盘通过周向均匀分布的12根拉杆预紧连接而成,压气机段包含15个盘间接触界面,用编号1～15表示,透平段包含5个盘间接触界面,用编号16～20表示。

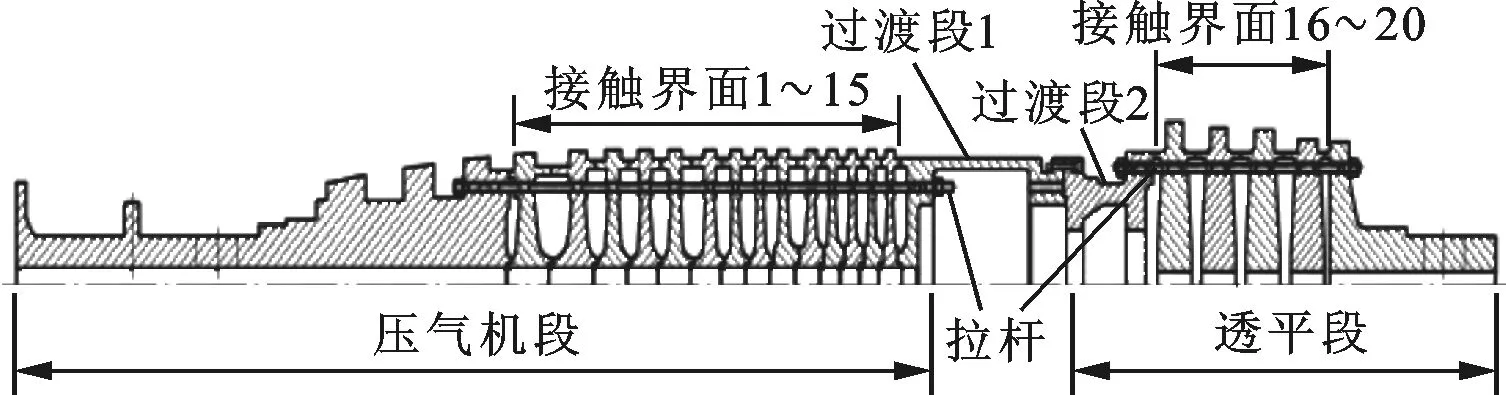
(a)燃气轮机转子几何结构

(b)燃气轮机转子有限元模型图1 本文燃气轮机转子模型

由于组合转子组构具有周期性,建立包含一根拉杆的1/12循环对称模型,组合转子选用材料Inconel718。该模型考虑了各轮盘间的环面、螺母头与轮盘、拉杆与拉杆孔、压气机轮盘间的止口配合4类接触,其中前2类采用允许分离的非线性粗糙接触模型,后2类采用允许相对滑动且无分离的线性接触模型,接触算法均采用罚函数法。此外,各接触界面设置为理想热接触,即两接触表面温度与热流密度相等。通过试算,综合考虑结果准确度、计算效率及接触面网格的精细处理,最终确定网格单元总数为29 616,节点总数为70 194。

1.2 力载荷与边界条件

图2给出了燃气轮机组合转子的多种运行工况,包含冷态载荷作用阶段及应用于燃气-蒸汽联合循环发电机组的一个常见典型工作循环。图2中x1～x5表示不同时刻,数字1、2分别对应不同冷态预紧力作用和冷态升速阶段,数字3～7对应典型工作循环中的稳态-停机-盘车-冷启动-稳态阶段。组合转子结构分析、热-结构耦合分析中所施加的力与边界条件描述如下。

(1)冷态预紧力。参考文献[1],压气机转子依靠接触面摩擦传扭,按80倍的压气机转子重力施加,等效为压气机拉杆伸长量的3.42%;透平转子采用端面齿啮合传扭,按100倍的透平转子重量施加,等效为透平拉杆伸长量的2.33%。第1阶段,压气机和透平段拉杆的预紧力变化范围分别为2%～3.41%和1%～2.33%。

(2)离心力。按图2所示转速施加离心力,额定工作转速为6 000 r/min。第2阶段,线性升速至额定转速。

(3)热载荷,即组合转子的温度场分布,以体载荷方式施加。在结构分析前,需先对组合转子的第3～7阶段进行热分析,获取温度场分布。瞬态热分析中的温度场时间步需与结构分析中的载荷步一一对应。

(4)力边界条件。组合转子压气机段的推力盘施加轴向约束,各级轮盘中心孔面施加旋转约束,以限制旋转自由度。

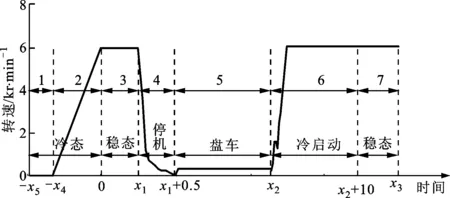
图2 组合转子的多种运行工况

1.3 热边界条件

组合转子的三维热分析需要提供热边界条件。由于组合转子的温度变化是通过压气机和透平主流道中的流体换热实现,因此热分析采用对流换热边界条件,即给定边界流体温度与对流换热系数。

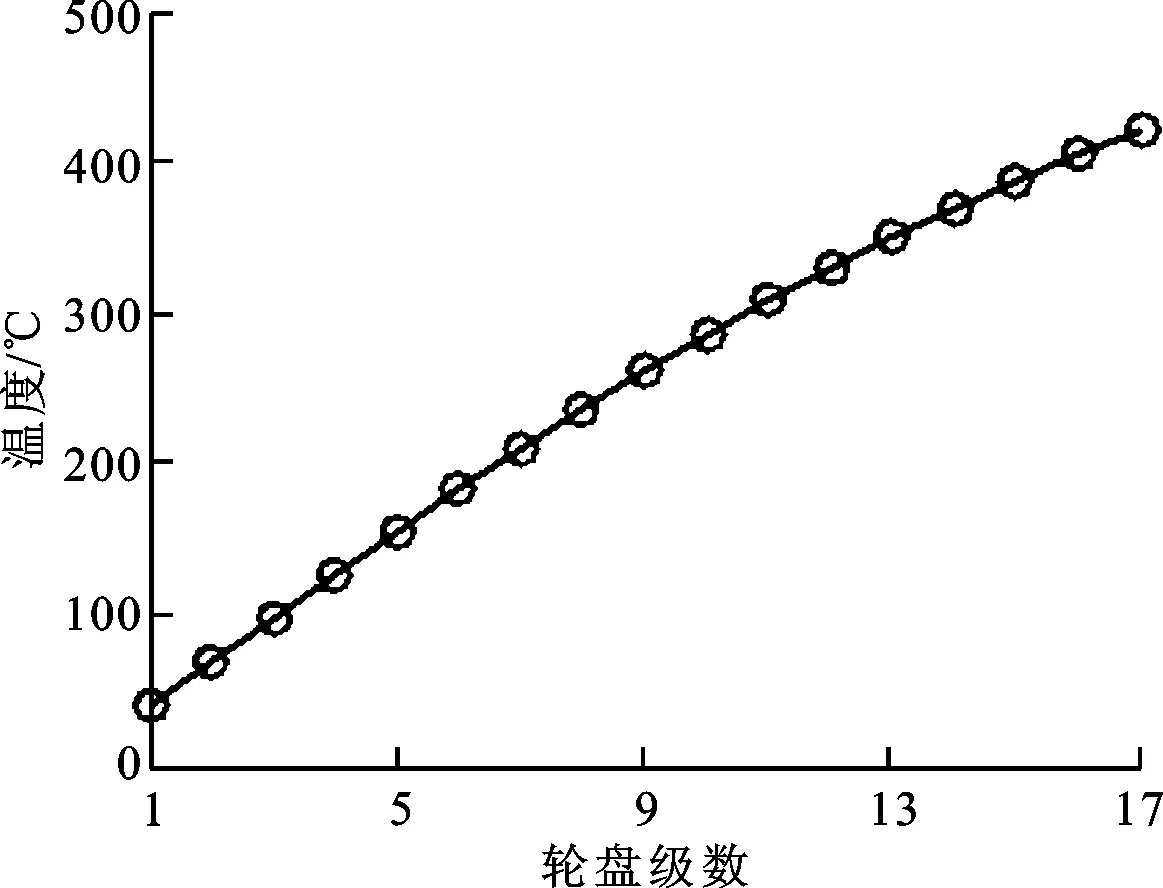
图3 压气机各级轮盘表面温度

1.3.1 稳态热边界条件 压气机各级轮盘边界压缩空气温度如图3所示。压缩空气与轮盘间的对流换热系数为[14]

(1)

式中:Re为雷诺数;Pr为普朗克数;λ为流体热导率,W/(m·K);D为轮盘外径,m。

透平段各级轮盘的冷却、密封气分别由压气机出口、压气机第4级、第8级和第12级抽气提供,因此透平轮盘边界流体温度为相应级空气温度。图4给出了透平段的3类对流换热腔室,分别是盘间接触界面以外形成的旋转腔、相邻轮盘与静叶持环内径形成的谜宫密封腔、相邻轮盘与静叶持环两侧面形成的左右动-静腔。

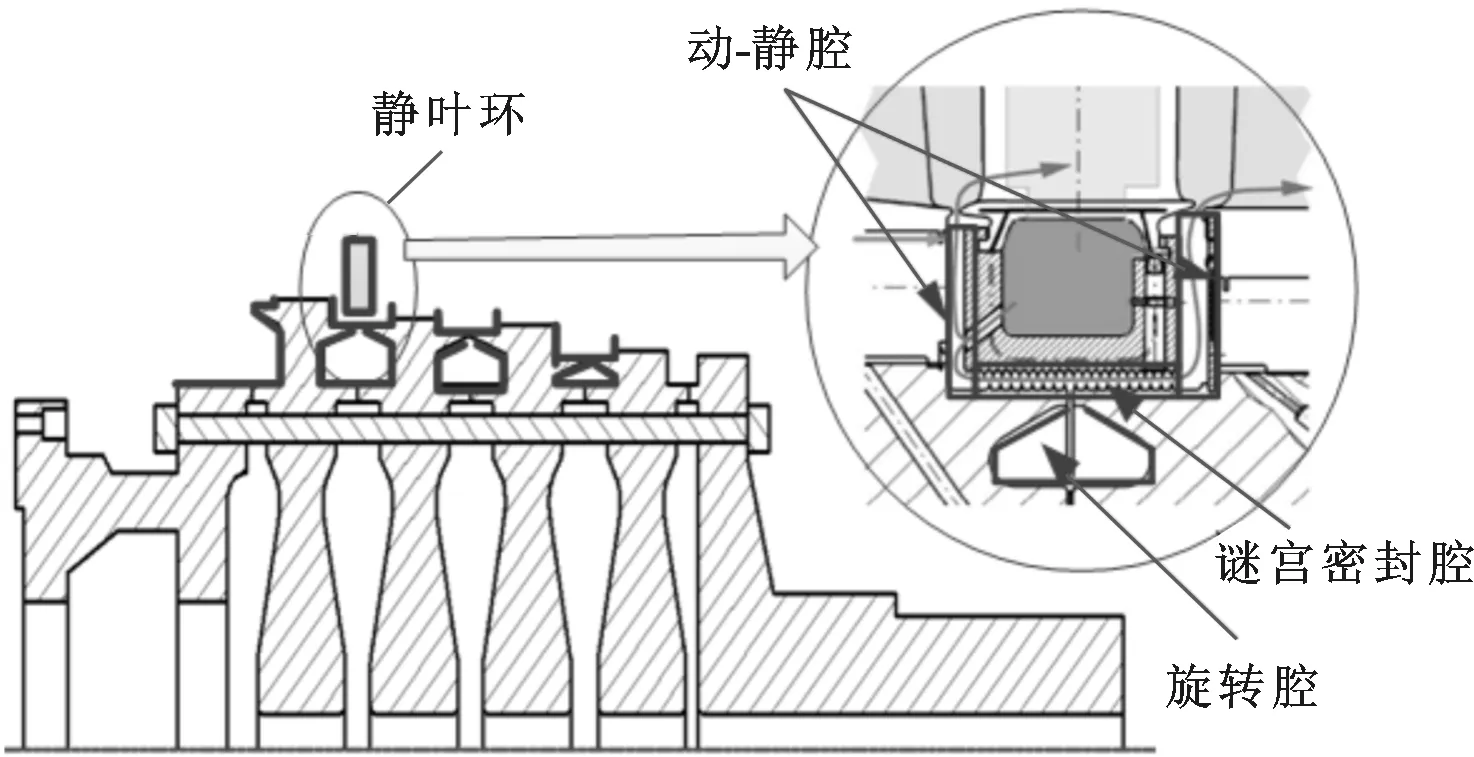
图4 透平端的3类对流换热腔室

旋转腔中的对流换热系数为[15]

(2)

Nu=0.069Gr0.333Pr0.407

(3)

(4)

ΔT=|Tdisk_i-Tdisk_i-1-1|

(5)

式中:Rest、Rint、Rmed分别为腔室外径、腔室内径和腔室中径,Rmed=(Rest+Rint)/2,m;Nu为努塞尔数;Gr为格拉晓夫数;Tmed为腔室中径处温度;Tdisk_i、Tdisk_i-1分别为相邻两级轮盘温度;T为相邻两级轮盘温度差的绝对值,K;ρ为气体密度,kg/m3;ω为转速,rad/s;η为流体动力黏度,Pa·s。

动-静腔中的对流换热系数为[16]

(6)

Nu=0.023Re0.8Pr0.333

(7)

(8)

Vrel=(1-XK)ωr

(9)

DH=2gap

(10)

式中:Vrel为流体与表面的相对速度,m/s;DH为特征长度,m;XK为气体当地周向速度与转子表面周向速度之比;gap为两平行表面之间的距离,m。

谜宫密封腔中的对流换热系数[16]选取周向对流换热系数与轴向对流换热系数中的较大值,即

h=max(hcir,hax)

(11)

(12)

(13)

(14)

Vrel=(1-XK)ωr

(15)

DH=2(ct+cs)

(16)

(17)

(18)

Re2=(WlDH)/(Afμ)

(19)

式中:ct为密封齿高,m;cs为密封齿径向间隙,m;Wl为谜宫密封处的气体流量,kg/s;Af为通流面积,m2;ha为轴向对流换热系数。

1.3.2 启、停机热边界条件 重型燃气轮机组合转子的大多数表面并未设置温度测点,因此获取启停过程中的边界流体温度变化是一个难点。本文基于文献[17]提出的缩放法,由稳态热边界条件经过相应的缩放公式来计算瞬态热边界条件。边界上的流体温度及对流换热系数缩放公式分别为

(20)

(21)

式中:T(t)、h(t)分别为边界上的流体瞬态温度及瞬态对流换热系数,W/m2K、K;TB.L、hB.L分别为边界上的流体稳态温度及稳态对流换热系数。θ(t)、α(t)分别为流体温度及换热系数缩放因子。由于压气机出口空气温度和透平排气口的燃气温度是实时监测,因此压气机段和透平段的缩放因子分别由二者的时变规律确定。环境温度为288.15 K。

转子冷启动由于始末温度场已知,式(20)不再适用,需计算冷启动过程中的边界流体温度。启动初始刻为环境温度(盘车时间长转子充分冷却),结束时刻为稳态温度场,假设压缩空气的温度变化与转速成正比,即

(22)

式中:T0为边界上的流体初始温度,K;N为额定转速;n为瞬态转速,r/min。透平段点火前,各级冷却空气温度为压气机对应级的抽气温度,点火后计算式为

(23)

式中:T1为点火时压气机相应抽气处的温度,K;n1为点火转速,r/min。

1.3.3 盘车热边界条件 盘车装置通常在转子停机后立即启动,使转子缓慢转动均匀冷却,防止发生热弯曲变形。盘车转速一般为每分钟数转,因此可忽略转速对转子与空气传热的影响,转子可看作周向均匀的自然对流冷却,对流换热系数为[18]

h=Nuλ/D

(24)

(25)

(26)

(27)

式中:ν为空气运动黏度,m2/s;cp为空气比热容,J/g·K;g为重力加速度,m/s2;β为体积热膨胀系数,对理想气体,近似等于1/Tf,Tf=(Ts+T∞)/2,Ts为热源温度(转子表面温度),T∞为流体最终温度,即环境温度为288.15 K。

1.4 初始温度条件

稳态热分析只需提供热边界条件,无需初始温度场,且得到的稳态温度场可作为停机瞬态热分析的初始温度场,故本文选用稳态作为典型工作循环的起始。同样,转子停机过程的末时刻温度场可作为盘车过程热分析的初始温度场,转子盘车末时刻的温度场可作为冷启动热分析的初始温度场。

2 稳态工况的接触应力分布

重型燃气轮机稳态运行时,同时受到预紧力、离心力和稳态温度场的作用,本节对预紧力单独作用(标记为P),预紧力与离心力作用(标记为PC),预紧力、离心力与稳态热载荷作用(标记为PCT)这3种加载方式下组合转子的盘间接触应力分布进行分析,进而讨论稳态温度场对盘间接触应力分布的影响规律。转子稳态温度场如图5所示,可知轴向温度不均匀,最高温度可达450 ℃,出现在过渡轴段,各轮盘内、外径温度基本相等。由于盘间接触应力均沿径向分布,取各个接触界面内径圆和外径圆上的接触应力来表示接触应力分布,分别用_i和_o来区分。

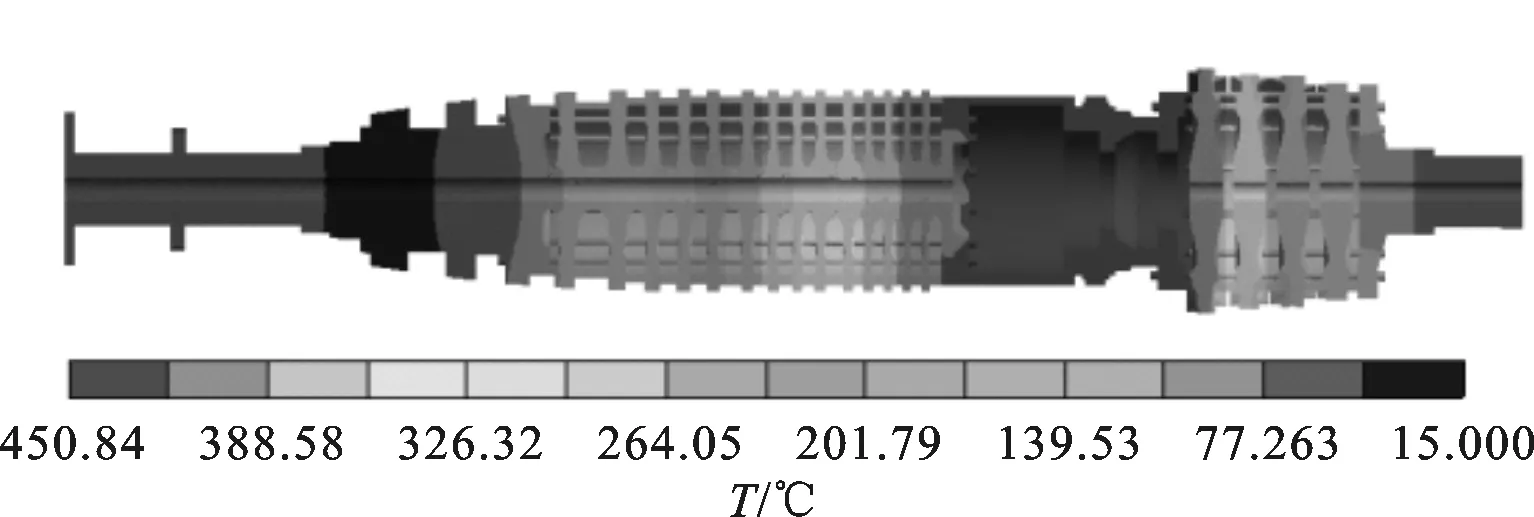
图5 转子稳态温度场分布

冷态盘间接触应力的理论均值可用来判断数值计算结果的可靠性,表达式为

(28)

式中:pm为冷态接触应力的理论均值,MPa;Fr为单根拉杆预紧力,N;m为拉杆数目;Ac为接触环面面积,mm2;R1、R2为接触环面内径圆和外径圆半径,mm,其中压气机段6～15号接触面的尺寸相同,透平段各接触面尺寸均相同。由式(28)可知,冷态接触应力均值与预紧力呈线性关系。

图6为3种加载方式下的各盘间接触应力分布。冷态接触均值的数值计算结果与式(28)确定的理论值吻合较好,验证了数值计算方法的准确性。预紧力、离心力和稳态温度场对各盘间接触应力分布影响的描述分别为:预紧力作用下,15号和16号接触面内、外径的接触应力差异最大,可见接触应力分布均匀性最差。离心力作用时,15号接触面的内、外径接触应力更靠近冷态均值,接触应力分布不均匀性得到改善,2号、16号接触面的接触应力分布不均匀性大大加剧,2号由于连接的环形段相对其他位置长度较长,因而受离心力的影响较大。稳态热载荷进一步作用时,除2、15、19和20号接触面外,其他接触界面的接触应力分布不均匀性并无明显变化。

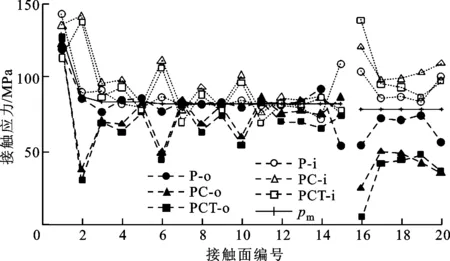
图6 3种加载方式下的盘间接触应力分布

图7为3种加载方式下的各盘间接触应力均值。由图7可知,离心力作用下,各盘间接触界面的接触应力均值均有所下降,这是由于拉杆在离心力作用下产生局部弯曲变形,拉杆因被拉长发生松弛,拉力降低,各盘间接触界面的接触应力均值相应下降。其中压气机端接触应力均值的降幅在2%之内,透平端的接触应力均值降幅达到8%,这是因为透平段拉杆分布圆直径更大,受离心力的影响松弛更大,拉力降幅更大,反映到接触应力均值上的降幅更大。稳态温度场在离心力作用的基础上,进一步降低了组合转子各轮盘接触界面的接触应力均值。这是因为轮盘的径向热膨胀使拉杆发生局部热弯曲变形,拉杆松弛,拉力降低,相应各盘间接触应力均值降低,其中压气机段的接触应力均值最大降幅为8.3%,出现在15号接触面,透平段的最大降幅为15.3%,出现在20号接触面。

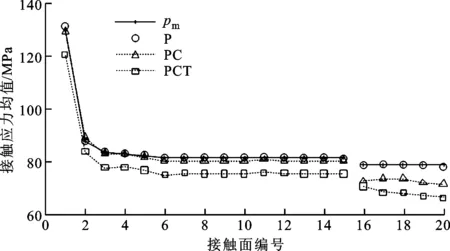
图7 3种加载方式下的盘间接触应力均值

3 瞬态工况的接触应力分布

本文转子模型中15、16号接触面最靠近高温过渡段的,也是接触应力分布均匀性在离心力和稳态温度场下表现相反的两个接触面,因而选取这两个关键接触界面作为重点分析对象,研究其接触应力分布在冷态及典型工作循环中的变化趋势,结果如图8、图9所示,各阶段的接触应力分布变化描述如下。

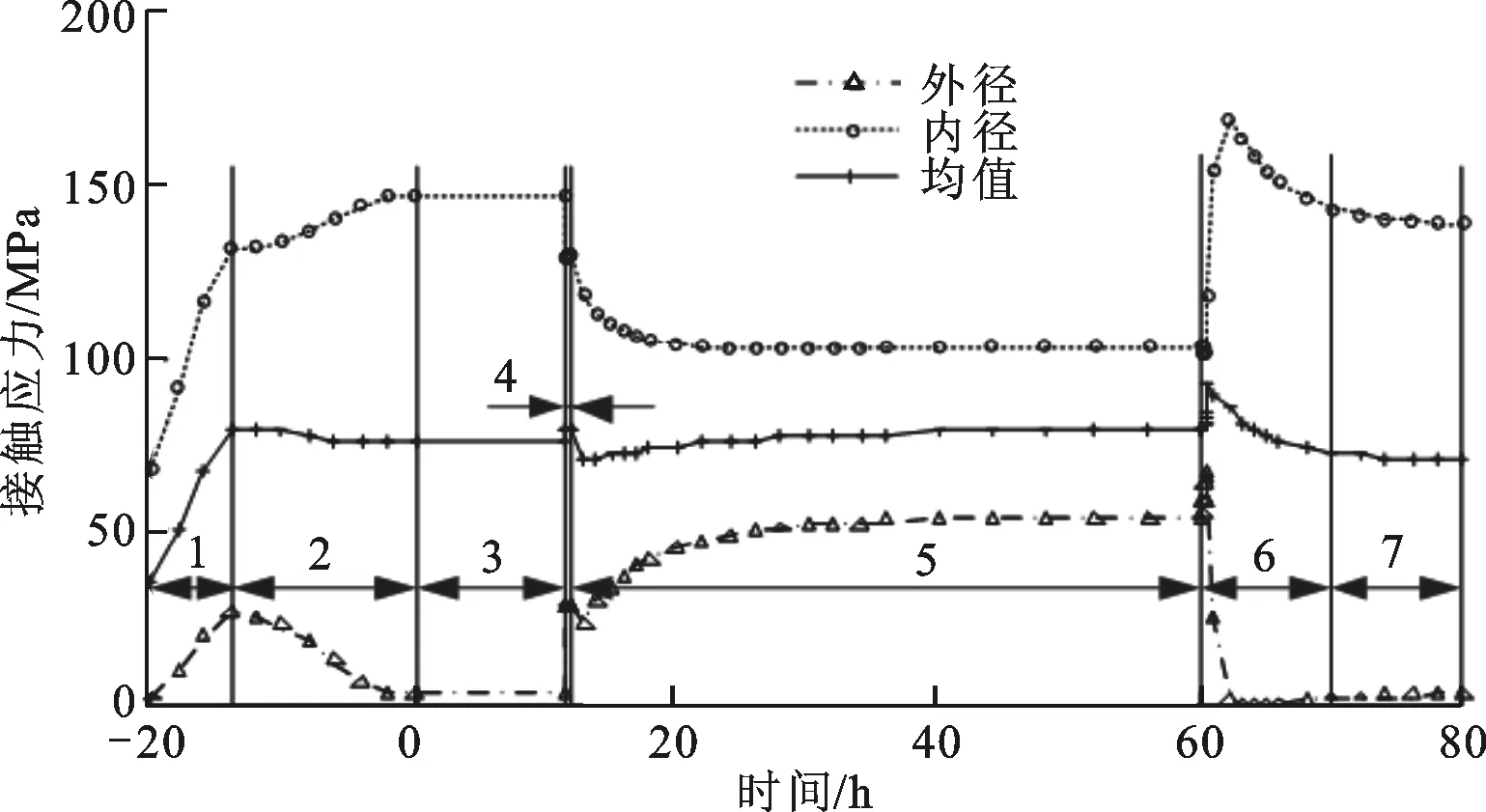
图9 16号接触面的瞬态接触应力分布

(1)第1阶段。随着预紧力的增大,15、16号接触面内、外径的接触应力均增大,接触应力均值增大,且接触应力分布不均匀性加剧。

(2)第2阶段。线性升速时,15、16号接触面的接触应力均值轻微下降,但分布不均匀性变化显著,前者大幅改善,后者加剧。

(3)第3、第7阶段。与最终冷态预紧的接触应力分布相比,15、16号接触面的稳态接触应力均值分别降低了7.7%、10.5%,15号的分布不均匀性有所改善,16号加剧。

(4)第4阶段。15、16号接触面的接触应力均值增大,几乎与最终冷态均值相等;15号的接触应力分布不均匀性加剧,而16号的有所改善。由于停机时间短,轮盘、拉杆温度变化小,接触应力分布的变化主要是离心力的影响,转速降低,离心力引起的拉杆局部弯曲变形减小,拉杆松弛逐渐消失,盘间接触应力相应均值增大;接触应力分布不均匀性的变化与第2阶段升速过程相反。

(5)第5阶段。因盘车中离心力的影响可忽略,盘间接触应力分布的变化为温度场单独作用结果。15、16号接触面的接触应力均值均呈先减小后增大的趋势,分别对应转子冷却的2个阶段:第1阶段,转子外部比内部冷却快,轮盘的轴向热膨胀比拉杆减小得快,拉杆有所松弛,拉力减小,盘间接触应力减小,最大降幅分别为13%、9.8%;第2阶段,随着时间推移,转子内外逐渐冷却至环境温度,拉杆与轮盘的相对膨胀量减小至零,盘间接触应力恢复至各自的冷态预紧分布。

(6)第6阶段。15、16号接触面的接触应力分布先后经历2个阶段。启动第1阶段,拉杆、轮盘温度升高,且轮盘温升快于拉杆,轮盘轴向、径向热膨胀量均大于拉杆,受拉杆限制,盘间接触应力增大,两接触面的接触应力分布与冷态相比,接触应力均值最大增幅分别为33.8%、17%,分布不均匀性变化最大;随后进入启动第2阶段,拉杆温度进一步升高,与轮盘间的轴向相对热膨胀开始降低,盘间接触应力降低,直至达到稳态分布。

组合转子冷态预紧的目的是为了使转子能抵抗其他载荷作用施加的分离力,并保持一定裕度,并不期望出现接触应力均值的降低;同时,极端工况下各连接界面100%完全接触及接触应力分布最大程度的均匀化是环面设计的极限追求。

4 结 论

对盘式拉杆组合转子进行了结构分析和热-结构耦合有限元法分析,得到了各盘间接触应力分布在冷态预紧、升速、稳态、启停及盘车等工况下的分布规律,主要结论如下。

(1)预紧力增大了各盘间接触界面的接触应力均值,同时加剧了接触应力分布的不均匀性。离心力使大多数盘间接触界面的接触应力分布不均匀性加剧,同时降低了接触应力均值,最大降幅为8%。

(2)稳态温度场引起的各盘间接触应力均值降幅各有差异,最大降幅约为15%。关键盘间接触界面的接触应力均值在冷启动过程中的最大增幅为33%,且接触应力分布不均匀性变化最大。从盘间接触应力均值和接触应力分布均匀性来看,热载荷是组合转子结构完整性的不利因素,在设计拉杆预紧力及盘间接触界面安全裕度时应充分考虑。