基于贝叶斯网络的智能电能表故障类型预测*

2018-11-13郑安刚张密曲明钰赵兵陈昊熊秋

电测与仪表 2018年21期

郑安刚，张密，曲明钰，赵兵，陈昊，熊秋

(1.中国电力科学研究院，北京100186； 2.北京邮电大学，北京100876)

0 引言

随着电力用户的不断增加，电力系统规模也得到很大的发展，智能电能表也因为其诸多优点得到了十分广泛的应用，智能电能表的推广应用不仅提升了电能计量和计费水平，还有效的防范了电费拖欠情况，提升了电力整体工作效率。但是受到运行环境、产品设计等因素的影响，智能电能表不可避免的会发生各类故障。在正常使用情况下，电能表会受到自然条件以及人为因素的影响，可能会导致故障，例如在自然情况下，一定时间内温度和湿度的异常可能会导致电子器件发生失效，在电能表的运行时间达到一定限度也可能会造成某种故障类型的发生；同样，不同电能表的厂商以及同一厂商不同批次生产的电能表发生某种故障的概率也不同，在这种情况下，利用机器学习方法，推断分析电能表故障的成因以及预测电能表风险故障类型也就成为了可能。

研究目的是实现对智能电能表故障类型的预测，在预测模型的研究领域，贝叶斯网络的表现尤为出色，在不同的领域上都有着不俗的表现：例如在突发事件预测上，某学者通过贝叶斯网络模型，以台风时间为例，成功构建了预测模型[1]。在航班延误的预测，某学者基于贝叶斯网络对问题得到了很好的解决[3]。在对于故障预测的领域，某学者提出了一种基于贝叶斯网络的预测方法[2]。一系列成功的案例也为文中的研究提供了十分有力的理论支持。目前国内对于智能电能表的故障分析主要在故障发生之后的研究，已经造成了不可挽回的损失。而对于智能电能表故障类型的预测工作并没有得到很好的进展，文中对于智能电能表故障类型的预测工作能够帮助预防和重视智能电能表相应故障的发生，具有十分重要的研究意义。

1 构建故障预测模型

从以往的研究可以看出，贝叶斯网络在预测领域上有着十分不俗的表现，本研究基于贝叶斯网络的方法，构建智能电能表故障类型的预测模型。主要的流程如图1所示。

图1 预测模型流程图

1.1 分析故障因素

分析故障因素的过程就是选取构建贝叶斯网络的节点的过程，在结合业务专家的意见下，通过对大量历史数据进行分析，寻找能够导致或者影响智能电能表故障类型的因素。

本实验研究的是电能表故障成因以及预测电能表故障，实验数据来源于某研究院计量中心。抽取了全国各地的电能表信息共计1 000万条，原始数据为到货批次信息，检定任务信息，全检综合结论信息，全检基本误差信息，现场运行故障信息，从中寻找筛选有价值的因素，在经过各方专家交流讨论和考虑现有的数据情况，将智能电能表的存放时间、运行时间、批次、供电所、厂商作为故障类型的影响因素加入到实验的分析中。

1.2数据预处理

实验选用存放时间、运行时间、批次、供电所、厂商、故障类型等因素，加入到网络的构建中。本研究基于不确定知识表达和推理技术，使用电能表故障数据构建贝叶斯网络模型，以直观的图形结构展现电能表故障各个层面的原因，方便对电能表故障中各个因素之间的关系进行分析评估。并能针对电能表故障信息对故障类型进行预测。但由于获取的数据在内容和格式不具备直接构建贝叶斯网络的条件，因此在构建贝叶斯网络之前需要对数据进行预处理，处理的方式如下：

(1)存放时间获取。实验中从检定任务信息和全检综合结论信息中获取的智能电能表检定时间和安装时间的差得到，并对差值进行量化分析。对于运行时间的获取，实验中从全检综合结论信息和现场运行故障信息的差值获取，同样对差值进行量化分析。数据格式如表1所示。

表1 运行时间和存放时间的编号

(2)对于批次、供电所、厂商信息的获取。实验中依次从到货批次信息中获取，首先是对数据进行筛选，将所需因素为空的数据进行删除，并将获取的信息进行编号量化，得到实验中可以使用的数据。部分数据格式如表2所示。

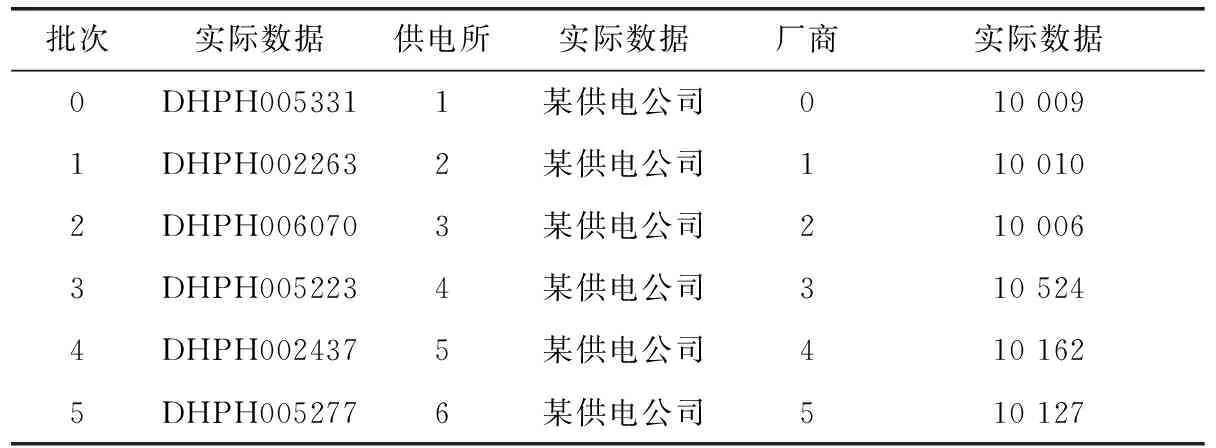
表2 批次、供电所、厂商对应实验数据

(3)对于故障类型的数据处理，由于考虑到实验数据中故障类型存在自然灾害这一情况，实验将这一故障类型清除，并对其他的故障类型进行编号处理，故障编号对应的数据见表3。

表3 故障类型对应标号

(4)对于智能电能表的内部因素的考虑。实验采用了电能表的设备规格和通信方式作为表3实验的影响因素，并从全检综合结论信息中获取相关数据进行相应的编号处理，得到实验所需的数据。处理后的数据形式如表4所示。

表4 预处理后的数据形式

1.3 构建贝叶斯网

贝叶斯网络又称为置信网，是在贝叶斯公式上拓展得到的不定性因果关联模型[4]，能够通过条件概率将各种相关信息纳入到同一个网络结构中，能够十分贴切的反应各个因素之间的因果关系和条件相关关系，可以在网络中任意节点已知的情况下，用贝叶斯网络规则在网络中进行正向或者逆向的推理，可以得到网络中其他节点的后验概率，因此，贝叶斯网络已经成为了推理领域上最有效的模型之一[5]。实验通过构建贝叶斯网络，在得知其他条件因素的情况下，对故障类型进行推理预测，在实际应用生产中达到预防或重点监测的作用。

目前主流的构建贝叶斯网络的方法大致分为两类：一类是评分-搜索算法，另一类是依赖分析算法。评分搜索算法过程简单规范，但是打分函数的运算复杂程度和结构空间的大小都随变量的增加指数增长，因此一般要求节点有顺序，并进行局部评分搜索，或者是采取随机搜索策略进行整体的评分搜索，适用于变量较少的稠密贝叶斯网络的结构学习；依赖分析方法过程比较复杂，但在一些假设下同样可以得到最优的贝叶斯网络，并且算法可具有多项式复杂度，适用于多变量稀疏的贝叶斯网络结构。由于目前所能获取的故障相关节点有限，因此本研究主要采用的基于搜索评分的构建贝叶斯网络的方法。

实验中构建贝叶斯网络的方法是基于K2算法[6-10]的贝叶斯网络结构学习。K2算法是比较优秀的评分-搜索算法，K2算法采用贪婪搜索处理模型选择问题：先定义一种评价网络结构优劣的评分函数，再从一个网络开始，根据事先确定的最大父节点数目和节点顺序，构建贝叶斯网络，K2算法的伪代码实现如下所示：

K2算法的伪代码实现

K2(X,Or,m,D)

输入：X={X1,X2,X3...XN}一组变量；Or-变量的顺序(与变量下标一致)；m-设定的最大父节点数；D-完整的数据集；

输出：贝叶斯网络；

1：Y—由节点X1,X2,...XN组成的无边图；

2：forj=1 ton

3:paj←φ；

4：Vold←CH();

5:while(true)

6:i←arg max1≤x|D)

7:Vnew←CH(|D)

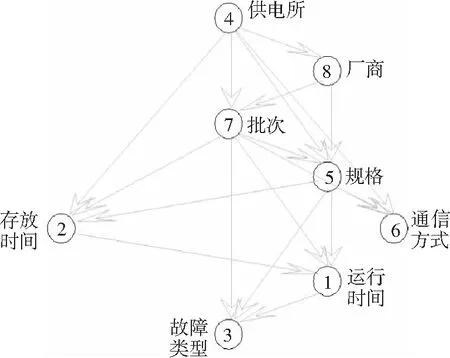
8:if(Vnew>Voldand |paj|

9:Vold←Vnew;

10:paj←paj∪{Xi};

11:在Y中加边Xi→Xj；

12:else

13:break;

14:end if

15:end while

16:end for

18：return(S,θ);

贝叶斯网络结构是为了计算而存在的，构建它的价值在于，假如存在了大量的历史数据，基于这些数据提供的先验知识构建完成了一个贝叶斯网络，在分析完成新的数据可能性任务时，在计算的时候，实验可以采用父节点的取值来预测相应节点的取值。本实验采用的有效实验数据为350 000多条，其中训练数据为320 000条， 30 000多条作为测试数据集。得到贝叶斯网络结构和条件概率表之后，将测试数据集中的故障类型进行人工缺失，利用其他节点信息结合贝叶斯网络对故障类型进行预测，并与原始数据进行比对，通过调整节点的顺序和最大父节点的数目，提高网络的准确度。

1.4 条件概率表

成因分析的任务可以解读为选择一定数量的特征属性，这些属性与表示故障的节点有着最大程度的关联，同时能够携带尽可能多的信息。成因分析模型中将以条件互信息作为衡量标准，以故障相关节点作为分类节点，衡量其余节点之间依赖关系的强弱。并对其余节点对类节点取值的影响信息给出定量的表示。根据条件互信息的定义，在给定某个节点作为类节点的情况下，去分析特定节点某个值的发生概率，通过贝叶斯网络结构和大量历史数据，可以获得故障类型节点的条件概率表，表明的是当父节点的某个取值的组合出现时，子节点对应取值的概率。这一条件概率表的意义在于，它简化了概率推理的计算。根据马尔科夫边界理论，一个节点的取值只需要考虑节点的父节点、子节点以及子节点的父节点。虽然直观上看来，节点的取值只受到一个父节点的取值的影响。但是，这不表示子节点只受到一个父节点的影响。

条件互信息表示的是在给定的类别下，随机变量之间互相影响的关系大小。成因分析模型中将以条件互信息作为衡量标准，以故障相关节点作为分类节点，衡量其余节点之间依赖关系的强弱。并对其余节点对类节点取值的影响信息给出定量的表示。根据条件互信息的定义，在给定某个节点作为类节点的情况下，去分析特定节点某个值的发生概率，通过贝叶斯网络结构和大量历史数据可以获得故障类型节点的条件概率表，表明的是当父节点的某个取值的组合出现时，子节点对应取值的概率。这一条件概率表的意义在于，它简化了概率推理的计算。

2 实验结果和分析

实验结果主要是考察贝叶斯网络结构对实验目标节点预测的准确度，进行了大量试验去调整贝叶斯网络结构使得智能电能表故障类型预测的准确率达到最高，以浙江省实验为例，实验共采用320 000条故障相关数据作为训练集，采用30 000条数据作为测试集，将测试集中的智能电能表故障类型一列进行人工缺失，通过训练集得到的贝叶斯网络结构对测试集中的电能表故障类型进行预测，将预测后的结果与原始结果进行比对，智能电能表的故障类型的命中率即作为实验的准确率。对于贝叶斯网络的预测实验需要首先得到最优的网络结构以及各节点的条件概率表，实验中得到的最优的网络结构如图2所示。

从以上实验得到的贝叶斯网络结构，可以看到“故障类型”节点的父节点有三个，分别是“批次号”、“运行时间”、“规格”。在此基础上，结合历史数据得到了故障类型在其他三个节点取不同值时的条件概率表。整个网络在构建过程中权衡了全部节点之间直接或间接的关联关系，最终出现的网络结构能够较好地表达变量之间的依赖关系。实验得到的条件概率表部分如表5所示。

图2 贝叶斯网络结构

故障类型批次运行时间规格发生概率45 122 0.818 862 5210 10 5 0.675 82528 5 2 0.235 1312 30.32613 4 31.010122 30.336 55410.68544410.818 181 818 2461210.25121050.1415650.857 142 8612941.0121940.729 302 32132540.122 448 9451230.288 56751030.916 66664820.833 333 4

最后通过实验得到的贝叶斯网络结构和条件概率表进行智能电能表故障类型的预测工作，采用30 000多条数据作为测试集，将测试集中的智能电能表故障类型一列进行人工缺失，通过训练集训练得到的贝叶斯网络结构对测试集中的电能表故障类型进行预测，将预测后的结果与原始结果进行比对，以下是实验中对二级故障测试集的预测结果如表6所示。

表6 测试集的预测结果

对于预测二级故障类型的实验，最优网络结构的准确率为65%，对于一级故障类型的实验准确率能够达到87%。贝叶斯网络的网络结构是为了计算而存在的，构建它的价值在于，假设已经存在大量的历史数据，基于这些数据提供的先验知识构建完成一个贝叶斯网络。在处理新的数据，完成分析故障类型的任务。在实验中选取准确率最高的贝叶斯网络结构进行参数学习，即故障类型的直接父节点为批次、运行时间和规格的情况。在计算的时候，可以采用父节点的取值来预测所需节点即可。由于原始数据就是所有的故障表，即智能电能表如果出现故障，且是这个批次，到达某个运行时间，哪种规格更容易出现什么样的问题和故障，针对这些条件因素来预测故障。在实际生产中可以根据已有的数据，对可能发生的故障类型进行预测，并有针对性的制定相应措施和开展故障运维，对于提升用电服务质量和用电可靠性具有很大的实际意义。