含电力电子装置电力系统戴维南参数频域特性研究*

陈姗姗，查晓明，黄萌

(武汉大学 电气工程学院，武汉 430072)

0 引 言

随着半导体技术的发展，大量的电力电子装置作为变换器或电子开关接入电力系统，电力电子装置以其功率密度高、控制灵活等诸多优点，在电力系统的发、输、配、用等各个环节得到广泛的应用。电力电子装置在电网中的渗透水平不断提高，电力电子化成为电力系统的重要趋势，电力系统正经历着深刻的历史性变革[1-2]。

电力电子装置在提高电网输电能力、改善电网运行状态的同时，也给电网的稳定带来了巨大的挑战。传统电网中，变压器、发电机是主要的谐波源，谐波含量较小，一般可以忽略不计。而在电力电子化电网中，电力电子装置是主要的谐波源，给电网造成较大的谐波污染[3]。电力电子装置产生的谐波一是源于其具有拓扑时变的特性，功率开关器件的开通和关断状态的组合对应不同的拓扑结构，二是由于电力电子装置中功率开关器件一般存在占空比控制，开关器件的占空比与状态变量的瞬时值相关。所以，电力电子装置成为了现代电网中又一种新的谐波源[4]。

戴维南等值是将电网等效为一个电压源与阻抗串联形式，是电网稳定性研究的重要方法之一[5-6]。在传统电网中，由于谐波现象不明显，仅考虑基波下的戴维南等值是可行的。但在电力电子化电网中，在基波条件下做电网的戴维南等效已不能完全反映实际电网的阻抗变化情况。因此，需要考虑戴维南参数的频域特性，关键问题在于戴维南参数的获得以及戴维南参数准确性的验证。

目前，已有的戴维南参数跟踪方法主要分为以下两种[7]：(1)网络解析法,按照戴维南定理求取开路电路和短路电流或通过导纳矩阵求逆的方法直接求取戴维南阻抗[8]；(2)基于潮流结果的方法，根据计算过程中使用的时刻点可以分为单时间断面法[9]和多时间断面法[10-11]。这两类方法考虑了稳态下、小扰动下及大扰动下的三类场景，但均是在基波条件下做电网的戴维南等效。戴维南参数的取值与负荷特性、故障扰动、发电机调节和系统控制等因素均相关[12-13]。系统接入若干电力电子装置后，若将其看成是一种特殊的负荷，则系统的阻抗特性会发生变化。

基于以上的情况，文中采用基于多时间断面法的电力系统戴维南等值参数计算方法，提出了一种电网在不同频率下戴维南等值参数表达的新形式。考虑电网中可能存在的大容量整流性负载情况，对一个含三相不控整流负荷的IEEE 9节点简单系统进行分析，发现其等值节点的戴维南阻抗参数与频率不存在正相关关系。通过对系统最大谐波功率传输能力进行仿真，验证了以上戴维南等效参数的有效性。

1 基于多时间断面的电网戴维南参数计算方法

对于第n次谐波，实际电力系统中，在时刻t从任一线性节点向系统看过去，均可把系统看成一个电压源经过一个阻抗向该负荷节点供电的两节点系统，如图1所示。这里取等值节点负荷模型为恒定电阻与恒定电感并联模型，ZnL的阻抗值仅与考虑的谐波次数有关。

图1 电力系统戴维南等值

图1中，对于第n次谐波，各电气量有如下关系：

(1)

式(1)中选用电压和电流进行计算，而不沿用文献[10]中用电压和功率进行计算，主要是基于以下的考虑：

(1)实际系统中谐波功率的测量较为困难；

(2)在谐波次数较大时，谐波功率和谐波电压的数值比较小，谐波功率往往达不到基波功率的1%，在采用标幺值进行计算时，功率和电压就更小了，在计算过程中可能会出现严重错误。

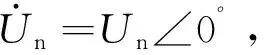
(2)

式中EnTHEV,r、EnTHEV,i分别为戴维南等值电势EnTHEV的实部和虚部；RnTHEV、XnTHEV分别为戴维南谐波电阻和电抗；In,r、In,i分别为等值节点负荷电流的实部和虚部。

该方程组有2个方程，4个未知数。因此必须再给定两个方程，一般认为当等值系统内部未发生扰动，仅等值节点侧发生较小的扰动时，两个运行点具有相同的戴维南参数。按照此思路在基态下给等值节点一定大小的扰动，由此得到基态附近的另一个运行点，采集这两个运行点的数据，该种方法即是使用较为广泛的多时间断面法[10-11]。

由式(2)可以得到：

(3)

根据式(3)即可计算出戴维南参数，如式(4)～式(7)所示。

(4)

(5)

(6)

(7)

其中：

多时间断面法跟踪方法基于两个运行点的戴维南参数相同的假定，因此其跟踪戴维南参数准确性的关键在于领域点的选取，等值节点处的负荷扰动太大，会使扰动后的采集数据与扰动前系统的运行数据偏差较大，计算得出的等值参数误差也会变大；扰动太小，则存在参数漂移现象，等值结果可能不正确。文中在实际算例中，采用扰动负荷功率的方式，扰动幅度小于2%。

2 算例分析

为探究含电力电子装置系统的戴维南参数的频域特性，以含整流装置的IEEE 9节点简单系统进行分析。

对于含电力电子装置的IEEE 9节点系统，建立阻抗解析模型十分困难，如何证明阻抗等值参数的准确性极具挑战性。

传统电网中，负荷阻抗减小时，电网阻抗和负荷阻抗逐渐接近，两者相等时，负荷功率取得最大值，电压达到崩溃点，这时，负荷阻抗再减小，功率也不再增加，电压迅速下降。故已有文献用阻抗模裕度来判断系统临界稳定状态[14]。

考虑某次谐波时，同样满足上述的最大功率传输定理，阻抗模裕度可以反映系统在该频率下当前运行状态离极限传输状态的距离。因此文中采用阻抗模指标的系统最大谐波功率传输仿真来验证戴维南参数等值的准确性。

扩展阻抗模裕度的定义，定义第n次谐波下的阻抗模裕度为：

(8)

当μn取0时，表示在该频率下系统运行在最大功率点；μn越小，表示系统离极限传输功率点越近。

2.1 仿真系统介绍

含整流装置的IEEE 9节点简单系统的系统结构拓扑如图2所示。

图2 9节点系统结构图

BPA暂态仿真程序采用基波相量进行计算，无法计及系统的谐波分析，而PSCAD采用时域分析，基于三相瞬时值进行计算，故采用PSCAD电磁暂态稳定程序作为仿真工具，在PSCAD平台下搭建系统。

各模型参数大体上参照IEEE 9节点系统中的参数，发电机为同步电机模型，均带励磁机，G2带稳定器，变压器采用双绕组变压器模型，输电线路采用集中模型。模型参数由BPA暂态仿真模型转换而来，转换方法参照文献[15]，BPA中未给出的参数按照默认值设定，主要参数如表1所示。

表1 IEEE 9系统主要参数

潮流计算中，各节点负荷均作为节点注入功率处理[10]，文中需要计及谐波分布，显然不适用。简便起见，负荷均采用电阻与电感的静态负荷模型，为了模拟含整流器的情况，母线B6负荷以功率为105+j20(MVA)的三相不控整流负荷代替标准系统中的负荷PL2，整流负荷不考虑滤波，PL1、PL3负荷均为电感、电阻恒定模型，负荷的电阻值和电感值根据标准系统中的参数计算而来，取基准容量为100 MW，基准电压为额定电压，负荷的阻抗标幺值如表2所示。

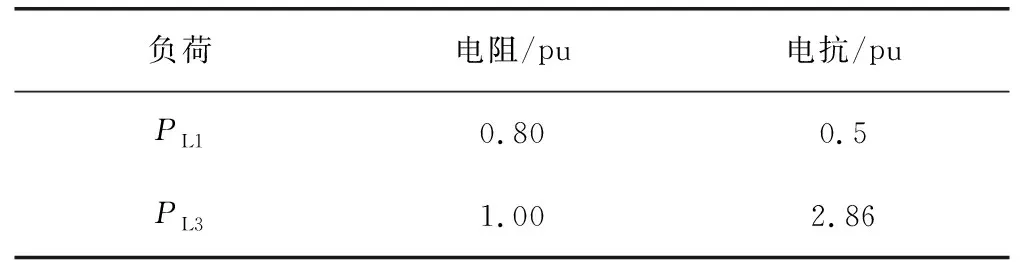
表2 负荷阻抗参数

利用IEEE 9节点系统接入三相不控整流负荷后，负荷母线B6处的波形畸变情况如图3所示。图4给出了某一负荷水平下母线B8处电压、电流和谐波分析情况。由图可知，系统主要含整数次谐波，不控整流负荷接入母线B6电压畸变较为严重，谐波含量达到了20%。与母线B6相比，母线B8处谐波含量较小。

图3 B6节点处谐波畸变情况

图4 B8节点处谐波畸变情况

2.2 戴维南等值结果

算例中，选择从负荷母线B8处进行戴维南等值，采用以上第1节提到的多时间断面法，已有文献中忽略了谐波，领域点按照一定程度的功率扰动给定[11]，文中需要计及谐波，故领域点按照等值节点负荷电阻扰动2%，电感保持不变选取，此时负荷侧的波动占主导。

三相不控整流负荷的谐波特征次为6k±1 (k=1, 2,3…)，以1, 5, 7, 11, 13次为例进行分析。采用PSCAD自带的FFT模块进行傅里叶分解，此模块采样1个基频周波的数据，带抗混叠滤波器，可以较为准确地输出整数次谐波的幅值和相位。

戴维南等值参数不是固定不变的，受负荷水平、网络拓扑、发电状况、运行模式等因素的影响[13]，文中探究不同负荷水平下电网戴维南等值参数与频率的关系。

文中采用的阻抗标幺值(R及XL)来表征等值节点负荷水平。图5给出了不同负荷水平下的戴维南谐波阻抗模。图5(a)中，负荷节点仅含R支路，改变电阻参数，通过戴维南等值得到了一系列谐波阻抗模。图5(b)是保持负荷节点电感不变，改变电阻参数得到的谐波阻抗模。图5(c)则是保持电阻不变，改变电感参数得到的谐波阻抗模。

图5 戴维南等值结果

从图5可以发现，改变等值节点负荷水平，谐波阻抗变化比基波阻抗变化稍大，但总体来说变化较小。尽管节点负荷水平不同，含大功率整流性装置的电网其戴维南等效参数的阻抗模值都具有随频率先增大后减小的非线性关系。这与传统电网戴维南等效阻抗X/R比值持续增大的情况完全不同。对于本算例来说，阻抗模最小值出现在基波频率下，大致为0.01 pu左右。阻抗模值最大值均出现在第7次谐波频率下，大致为0.8 pu～1 pu左右。

同时仅考虑某一谐波频率下的戴维南参数，发现保持电感不变减小电阻值，即增大等值节点负荷，谐波阻抗模逐渐增大；保持电阻不变，增大电感值，5次、7次处谐波阻抗模逐渐增大，但11次、13次处增大趋势不明显。

2.3 结果验证

等值节点负荷水平为R=0.55 pu，XL=0.06 pu时(即负荷水平一)，戴维南阻抗模与负荷阻抗模的取值如表3所示。

表3 负荷水平一时负荷阻抗模及戴维南阻抗模

由表3可知，n=5时，Zn,L和ZnTHEV模值近似相等。按照阻抗模裕度指标来检验5次下谐波阻抗的准确性，保持等值节点负荷电感不变，改变等值节点电阻，n=5时有功功率、戴维南参数及阻抗模裕度指标如表4和图6所示。

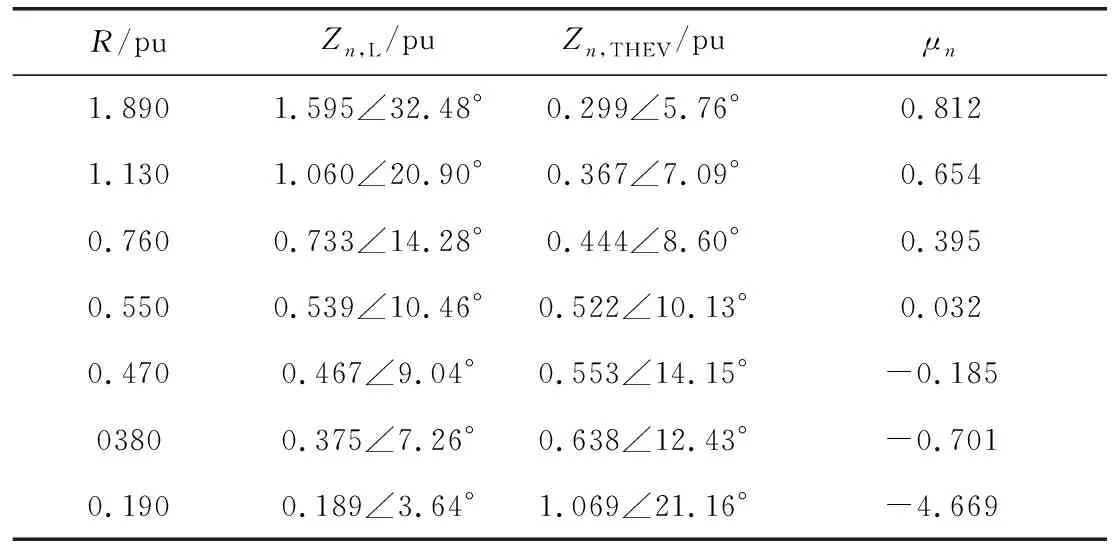
表4 n=5时，不同负荷水平下的阻抗模指标

图6 n=5时，不同负荷水平下的戴维南参数

仅考虑n=5时，随负荷水平增加，负荷阻抗模和谐波阻抗模逐渐接近，阻抗模裕度μn减小，当负荷水平为R=0.55 pu，XL=0.06 pu时，μn为很小的正数0.032，线路传输的该次有功功率达到最大值，达到电压崩溃点。这时，负荷水平再增加，阻抗模裕度由正数变为了负数，有功功率不再增加。

在等值节点负荷水平为R=0.95 pu，XL=0.12 pu时(即负荷水平二)，戴维南等值阻抗模与负荷阻抗模的取值如表5所示。

表5 负荷水平二时负荷阻抗模及戴维南阻抗模

n=7时，Zn,L和ZnTHEV模值近似相等。同样保持等值节点负荷电感不变，改变等值节点电阻，n=7时有功功率、戴维南参数及阻抗模裕度指标如表6及图7所示。

当负荷水平为R=0.95 pu，XL=0.12 pu时，线路传输的该次有功功率达到最大值。

表6 n=7时，不同负荷水平下的阻抗模裕度

图7 n=7时，不同负荷水平下的戴维南参数

在等值节点R=0.55 pu，XL=0.03 pu的负荷水平下(即负荷水平三)，谐波阻抗模与负荷阻抗模的取值如表7所示。

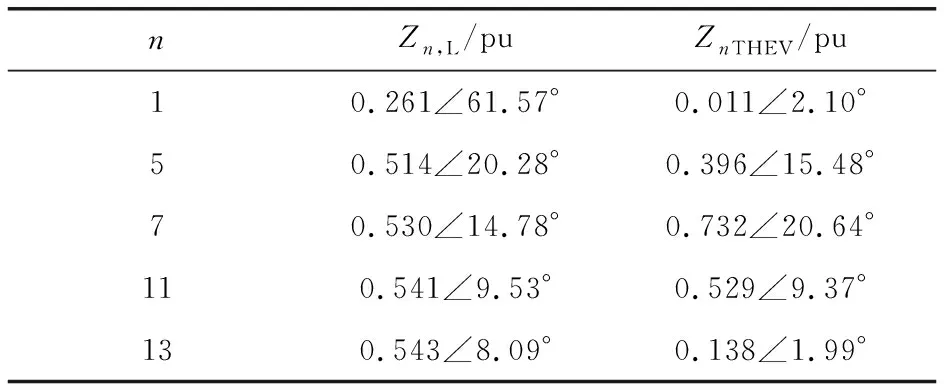
表7 负荷水平三时负荷阻抗模及戴维南阻抗模

n=11时，Zn,L和ZnTHEV模值近似相等。因此保持等值节点负荷电感不变，改变等值节点电阻。n=11时有功功率、戴维南参数及阻抗模裕度指标如表8和图8所示。

表8 n=11时，不同负荷水平下的阻抗模裕度

图8 n=11时，不同负荷水平下的戴维南参数

由图8可知，Zn,L和ZnTHEV在R=0.55 pu，XL=0.03 pu时达到负荷匹配状态，传输的第11次谐波功率达到最大。

在等值节点R=0.20 pu，XL=∞的负荷水平下(即负荷水平四)，戴维南等值阻抗模与负荷阻抗模的取值如表9所示。

表9 负荷水平四时负荷阻抗模及戴维南阻抗模

n=13时，Zn,L和ZnTHEV模值近似相等。因此仅改变等值节点电阻参数，n=13时有功功率、戴维南参数及阻抗模裕度指标如表10和图9所示。

由仿真结果可知，在R=0.20 pu，XL=∞时，谐波阻抗模与负荷阻抗模接近，μn基本为0，此时，系统传输的第13次谐波功率取得最大值。

从以上阻抗模指标的仿真结果可以看出，在研究的系统中，戴维南阻抗与频率为非正相关关系，各次谐波频率下的阻抗模值分别如图6～图9所示。

表10 n=13时，不同负荷水平下的阻抗模裕度

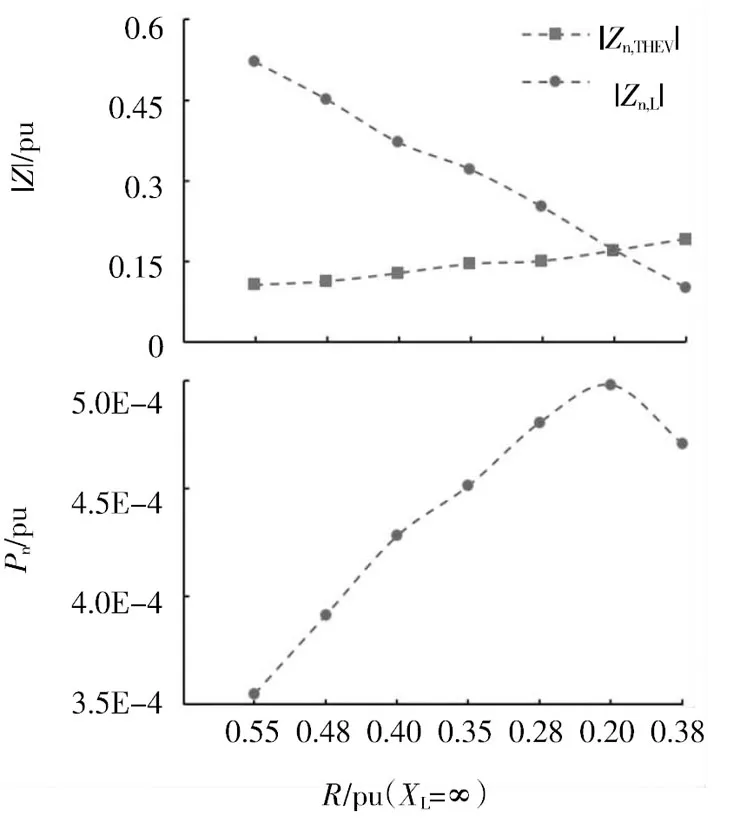
图9 n=13时，不同负荷水平下的戴维南参数

综合以上分析，可以发现，该系统阻抗模值在7次谐波频率下取得最大值，与第2节中的分析结果完全一致。因此，分析中采用多时间断面法得到的戴维南等值结果是准确的，戴维南阻抗与负荷阻抗匹配时，在对应频率下的谐波功率取得最大值。

3 结束语

考虑到电力电子装置的高渗透给电网带来的影响，提出采用基于多时间断面法的电力系统戴维南等值参数计算方法，给出了电网不同频率下戴维南等值参数表达通过对含整流装置的IEEE 9节点简单系统进行分析，发现其等值阻抗与频率为非正相关关系。分析结果通过基于阻抗模指标的电力系统最大谐波功率传输能力进行了验证。所提出的等值算法能够应用于不同频率下的戴维南参数计算，更好地反映实际电网阻抗变化情况，具有一定的实用价值。