基于罗氏线圈的VSC-HVDC系统的混合线路故障定位*

汪磊，刘辉，邱诗怡，姜晓彤，钱金良

(湖北工业大学 电气与电子工程学院，武汉 430068)

0 引 言

基于电压源换流器的高压直流输电(Voltage Source Converter HVDC, VSC-HVDC)具有独特的技术优点，它在向偏远地区负荷供电，城市配电网增容改造，提高配电网电能质量等方面发挥着积极的作用。同时，该技术可以将海上风力发电产生的大量电能从海洋传输到远距离的陆地[1]。在海上使用海底电缆而在地面上使用架空线路，这种混合线路的系统因长距离输电发生线路故障的概率比较大而且巡线的难度很大，实现及时准确地故障定位具有重要的研究价值。

高压直流输电故障测距的方法主要可以分为故障分析法和行波法[2]。故障分析法是通过计算分析系统参数和测量的电压、电流，求出故障点的距离。文献[3]和文献[4]中都是先通过双端电压和电流的测量然后分别根据Bergeron分布式参数模型和二端口理论来建立方程并求解来实现故障定位。在文献[5]中提出用单端相位测距法和单端幅值测距法实现故障测距。文献[6]中由Fourier变换来估计观测点到故障点之间的阻抗，经过反复迭代后得出比较精确的故障点。但是文献[3-6]中对线路参数的计算精度要求较高，这些参数的误差对故障定位的精度影响较大。行波法在高压直流输电故障定位中使用较多而且其研究主要在波头识别和波速选取上。文献[7]中提出将行波法与固有频率法结合起来的单端故障测距算法，解决了波速选取的难题，但是没有解决过渡电阻的影响。文献[8-9]和文献[10]中分别用Hilbert-Huang变换和数学形态学的方法来识别波头，但是没有考虑抗干扰性能。对于该混合线路的研究，在文献[11]中提出了基于双端行波测距原理的小波分析方法。在文献[12]提出先利用支持向量机(SVM)识别故障区段再利用离散小波变换(DWT)进行单端故障定位。在文献[13]中提出一种基于故障长度占比的混合线路故障行波定位新方法，解决了波速与线路长度的参数整定问题。

文献[14]中通过研究直流输电线路电流及电压高频小波能量暂态特性解决了区分内外的故障以及选取故障极的问题。在文中只考虑直流输电线路单极接地的故障情况。根据双端行波法测距的原理，在仿真软件PSCAD/EMTDC中搭建仿真模型，采用Rogowski线圈来获取浪涌到达时间，实现对线缆混合线路的故障测距。不仅避免了受故障电阻或故障类型的影响而且计算简单，适用性很强。

1 VSC-HVDC系统结构

双端VSC-HVDC输电系统的主电路如图1所示。其中电压源换流器主要部件包括：全控换流桥、直流侧电容器、交流侧换流变压器以及交流滤波器。其中全控换流桥采用三相两电平的拓扑结构，每个桥臂均由多个IGBT组成。

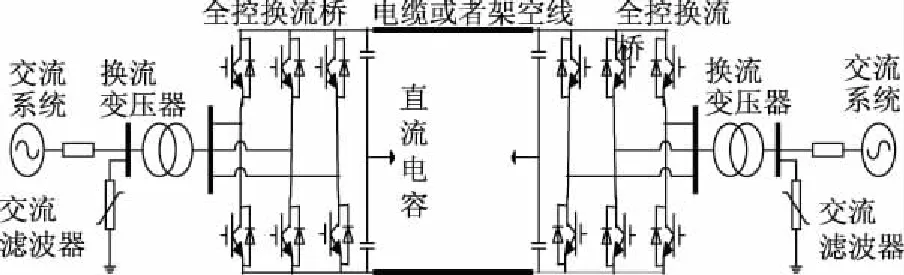
图1 VSC-HVDC的基本结构

该系统中间的直流输电线路可以取电缆或者输电线，取两者的混合形式。主要有两种情况，如图2和图3所示。

图2 两段式混合VSC-HVDC系统

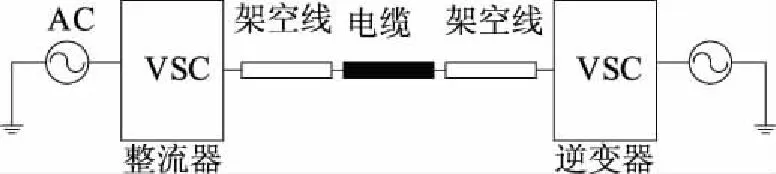
图3 三段式混合VSC-HVDC系统

2 混合线路测距原理

2.1 两段式线路行波测距原理

以图4来说明一下，当故障发生时，故障点将向两端产生行波，行波遇到终端1、2或者混合线路的交接点处将同时产生反射和折射。同时，行波通常在架空线上的速度接近光速，而在地下电缆的速度约为光速的三分之二。不妨假设电缆上的行波速度为v1，架空线上的行波速度为v2。

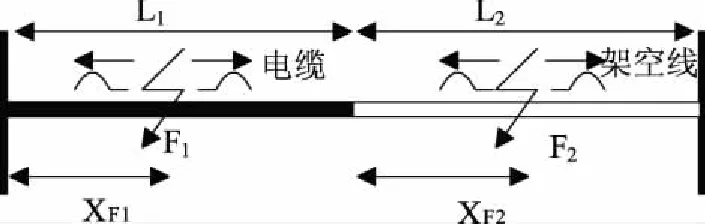
图4 故障分别发生电缆和架空线的F1处和F2处

当只有F1处发生故障时，行波到达终端1、2的时间分别为t1-F1、t2-F1则有：

(1)

(2)

式中XF1为F1到终端1的距离；L1、L2分别为电缆和架空线的长度。为了实现双端行波测距，需要联立式(1)和式(2)，我们引入Δt则有：

(3)

由式(3)可得故障距离XF1为：

(4)

同理当F2发生故障时，有式(5)～式(8)：

(5)

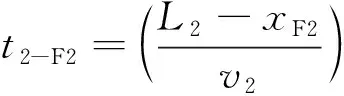
(6)

(7)

(8)

式中XF2为F2到混合线路交接点的距离。图5的流程图是故障测距的具体算法。在文献[12]和文献[15]中利用支持向量机(SVM)对于故障区段进行识别，显然文中的算法更简便。

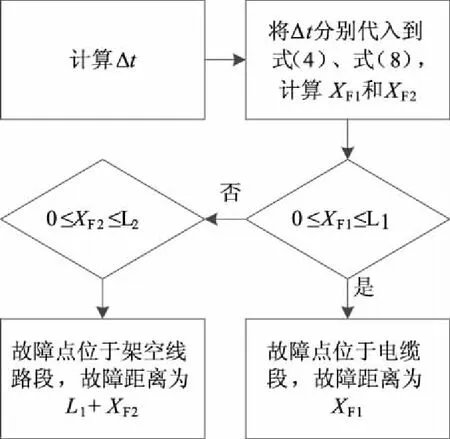
图5 两段式线路故障测距的算法

2.2 三段式线路行波测距原理

如图6所示，三段线路上的行波速度分别为v1、v2和v3。三段式线路与两段式线路的分析方法类似，同理可以得出式(9)～式(11)。

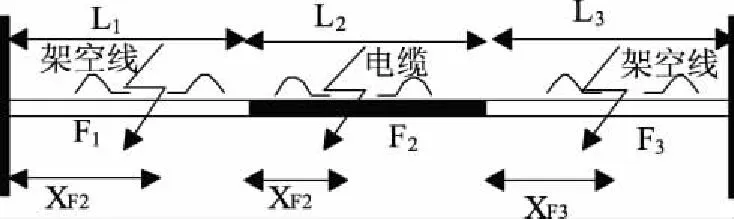
图6 故障分别发生在F1、F2、F3处

(9)

(10)

(11)

图7流程图是故障测距的具体算法。

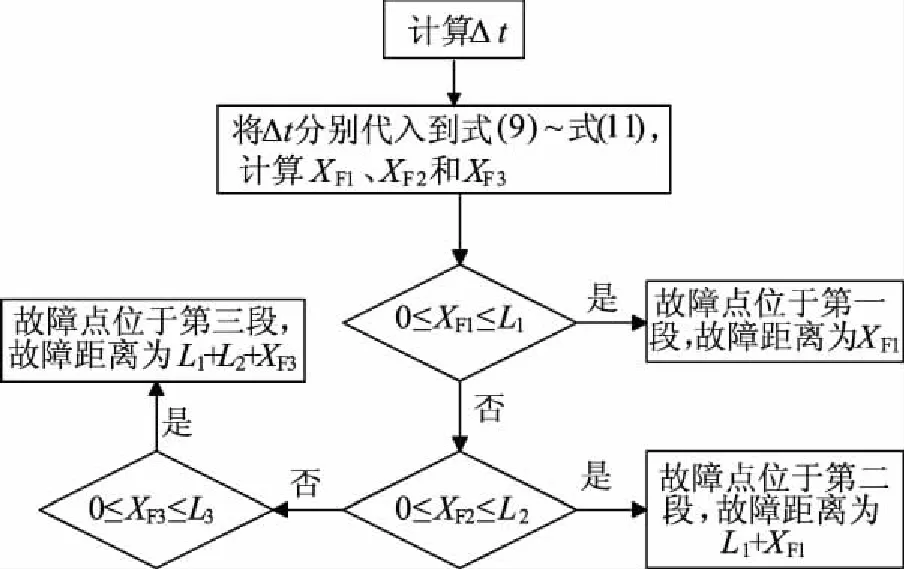
图7 三段式线路故障测距的算法

2.3 测量两端时间差的方法

Rogowski线圈用在行波法线路故障定位中具有可行性，且它具有简单性等优点[16]。它能测量几安到几千安的电流，且不容易达到饱和。线圈输出的电压e(t)与输入电流i(t)的变化率成正比，如式(12)所示。其中M是Rogowski线圈的互感：

(12)

当测量恒定的直流电流时，显然输出的电压为零。可以通过观察Rogowski线圈输出电压的波形来确定浪涌波头到达两个终端的时间，进而得出Δt，具体的过程将在第3部分给出。

2.4 双极线路的解耦分析

对于含有双极线路的VSC-HVDC输电系统来说存在着相互耦合的问题，而且参数具有频变特性，为了消除这些因素的影响以便于简化计算，可以考虑用模量分析的方法[17]。其具体的处理方法为：

(13)

式中im0、im1分别表示解耦之后的0模和1模的电流，iP、iN分别表示对应的正极和负极的电流，S表示解耦矩阵。在文献[18]中提到1模量行波的速度随频率变化小，而0模量行波的速度随频率变化较大，且前者的速度大于后者，同时在文献[19]中说明了1模量参数比0模量稳定，因此在双极运行方式下，应该取1模量的电流进行分析，来进一步确定波头达到的时间。

3 仿真模型搭建及相关参数

如图8所示，在PSCAD / EMTDC中搭建两段式VSC-HVDC系统的仿真模型，采用直接电流控制的双闭环串级PI控制器[20]。其中左侧的送端系统由三相电压源模拟，主要参数为线电压110 kV，系统为阻抗1.7 Ω。变压器采用Yn/Δ联结，其容量为25 MVA，绕组电压110 kV/25 kV，漏抗0.2 pu。相电抗器为0.053 H，等效电阻0.8 Ω。右侧受端系统也由三相电压源来模拟无穷大系统，其系统阻抗为0，线电压110 kV。变压器采用Yn/Δ联结，其容量为20 MVA，绕组电压110 kV/25 kV，漏抗为0.1 pu。相电抗器为0.053 H，等效电阻0.6 Ω。考虑到参数的频变特性，该模型中的电缆和架空线选用的都是Frequency Dependent(Phase) Model即频率相关相域模型，其电缆和架空线的参数如图9所示，其中电缆的电阻为1.72×10-8Ω·m，绝缘子相对介电常数为2.5，长度为350 km；架空线的电阻为0.032 06 Ω/km，长度为350 km。在PSCAD中编程得到进行模变换的解耦电路，如图10所示。罗氏线圈模型如图11所示。

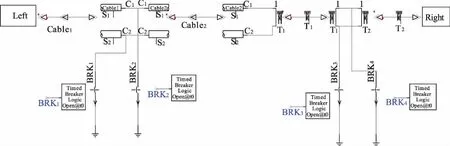
图8 整体仿真模型图

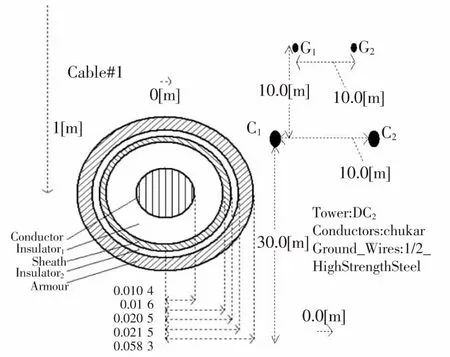
图9 电缆和架空线的参数

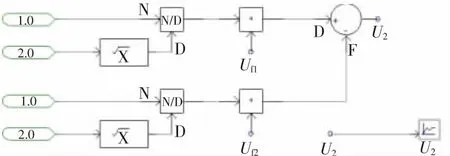
图10 模变换的解耦电路模型

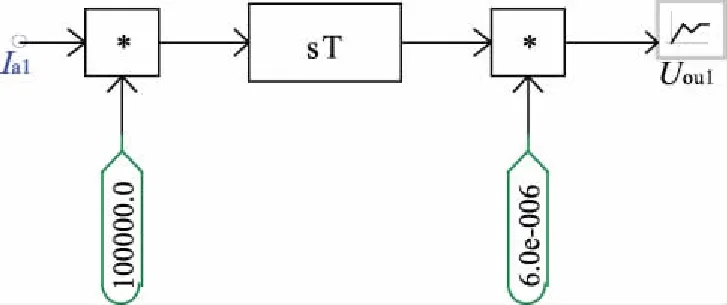
图11 罗氏线圈的模型

为了能提高对罗氏线圈输出电压的波形的分辨能力，还需要在供电侧(1侧)和受电侧(2侧)分别串联一个电感，同时在要并联一个浪涌接地电容，如图12所示。先分别取供电侧和受电侧的两极电流进行模变换，然后将1模量的电流导入到罗氏线圈。

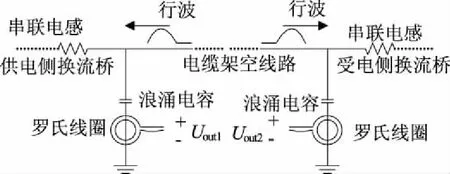
图12 供电侧和受电侧测量电路原理图

4 仿真结果及分析

在130 km处设置单相(正极)接地故障，故障发生的时刻为2.0 s且持续时间为0.05 s。利用罗氏线圈测量1侧的正极的电流。若要考虑到串联电感的大小以及浪涌电容的大小是否可能对测量的结果产生影响的情况。取浪涌电容为1 mF，串联电感分别取为1 mH、10 mH、100 mH分别在PSCAD上进行仿真以及取串联电感为1 mH，浪涌电容分别取为0.1 mF、1 mF、10 mF分别在PSCAD上进行仿真，得出1侧的罗氏线圈测量电流后输出的电压的波形，并把这几种情况的数据导入Matlab，在同一张图上绘出了这些波形，如图13和图14所示，由图可以清楚地观察出线圈输出电压信号最开始发生畸变的时刻基本上是相同的，其误差可以忽略不计，进而可以得出该信号畸变的时刻是与串联电感以及浪涌电容均无关的结论。

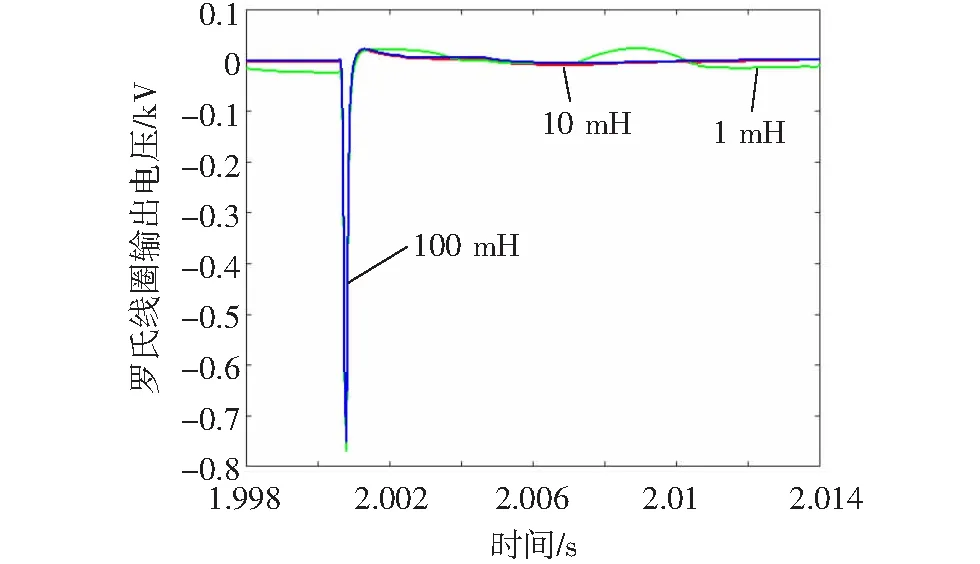
图13 不同串联电感情况下罗氏线圈在1侧的输出电压

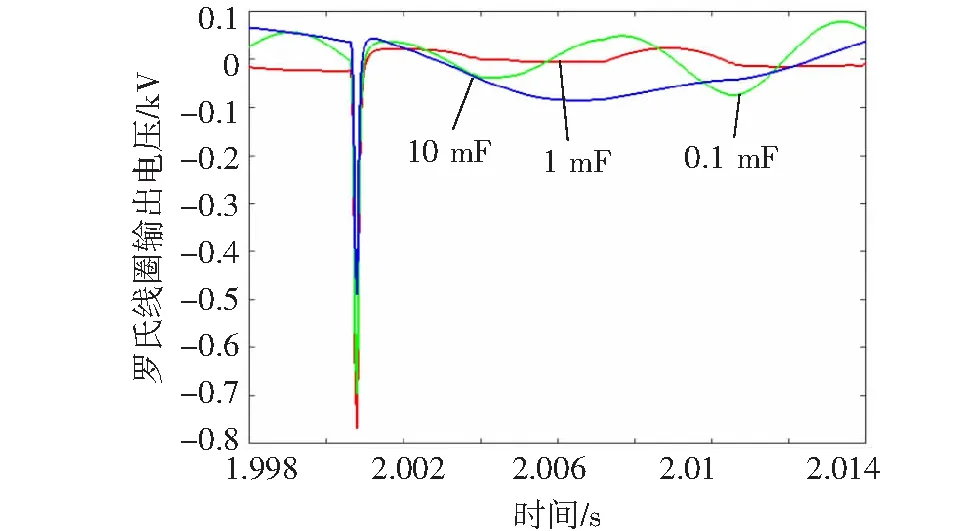
图14 不同浪涌电容情况下罗氏线圈在1侧的输出电压

不妨令串联电感取1 mH，浪涌电容取1 mF。如图15和图16所示,Uout1和Uout2分别为罗氏线圈的输出电压，这里可以通过PSCAD的图像窗口读出线圈输出电压信号最开始发生畸变的时刻分别为t1-F1=2.000 698 2 s和t2-F1=2.002 381 s。这些畸变的初始时刻就是行波的波头首次到达1侧和2侧的时刻。显然，Δt=t2-F1-t1-F1=1.682 8 ms。无论是两段式还是三段式的系统都能用这种方法求出Δt，根据上面分析的算法可知接下来的工作是求出行波传播速度v1、v2。

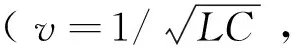
图15 罗氏线圈测量1侧的电流

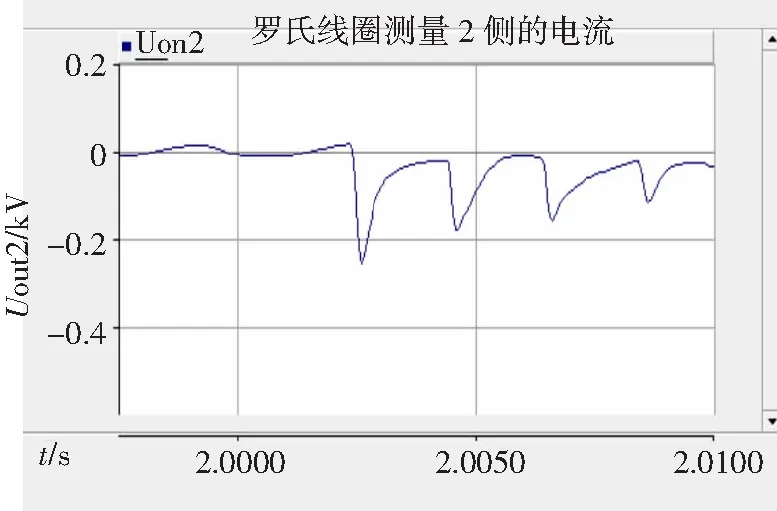
图16 罗氏线圈测量2侧的电流

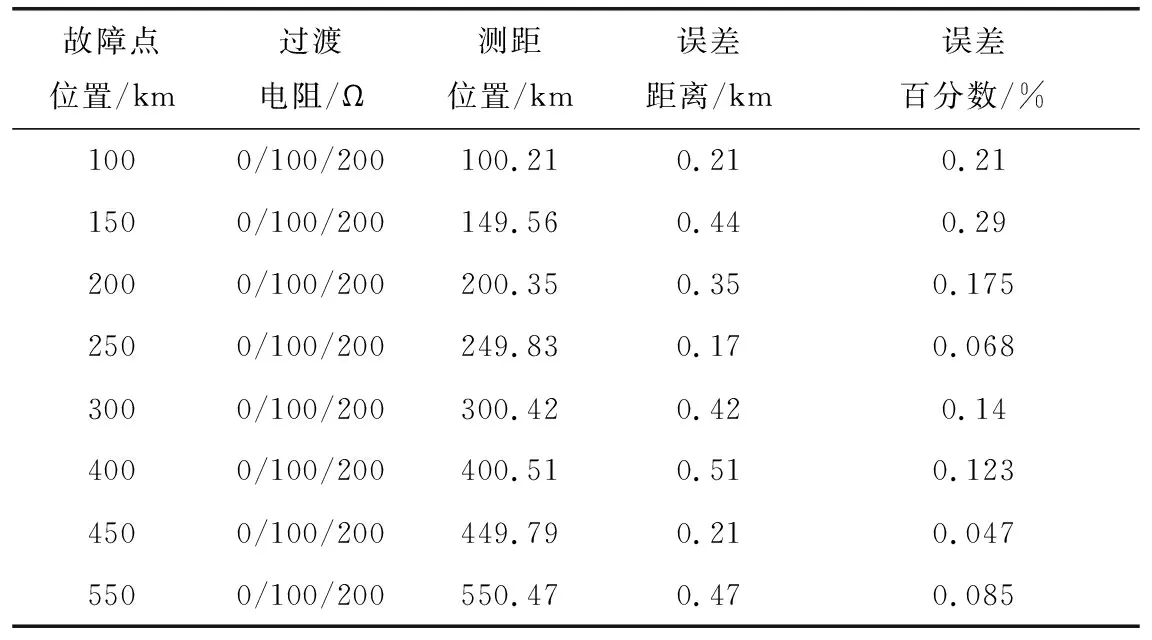
故障点位置/km过渡电阻/Ω测距位置/km误差距离/km误差百分数/%1000/100/200100.210.210.211500/100/200149.560.440.292000/100/200200.350.350.1752500/100/200249.830.170.0683000/100/200300.420.420.144000/100/200400.510.510.1234500/100/200449.790.210.0475500/100/200550.470.470.085

由三段式线路故障测距的算法，同样可以得出不同故障点以及不同过渡电阻情况下的故障定位结果如表2所示。

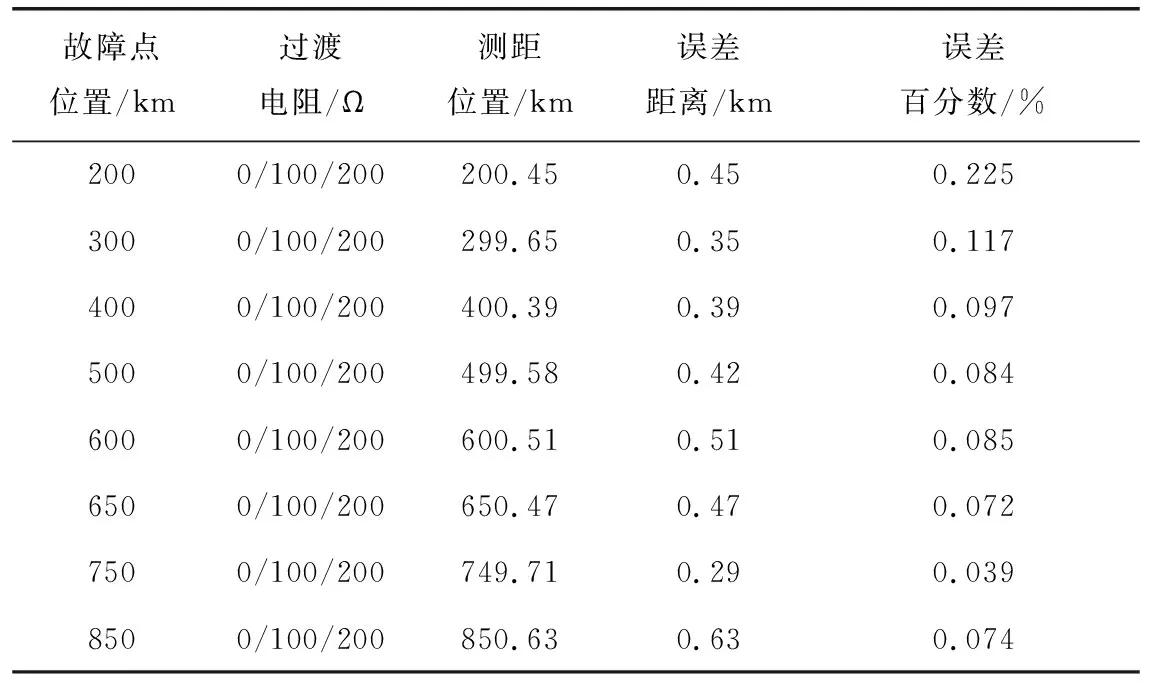
表2 三段式线路不同故障点和过渡电阻时的测距结果

由表1和表2中的数据可以看出两段式和三段式线路故障测距的最大误差百分数分别为0.29%和0.225%，可知基于罗氏线圈识别波头的方法在高压直流输电混合线路中能达到比较精确的故障测距效果，而且受到过渡电阻的影响较小，该算法原理比较简单，配合GPS时间同步系统，更容易设计出故障测距的软硬件系统 ，非常具有实用价值。

5 结束语

根据双端行波测距的原理，提出了针对两段式和三段式的VSC-HVDC的电缆-架空线混合线路的测距的算法，且该算法简单可行，利用罗氏线圈测量电流分析输出电压的波形来识别波头，得出比较精确的波头到达两端的时刻，克服了故障分析法中参数计算精度要求高和单端行波测距识别波头的难题，故障测距精度高，且抗干扰性能较好。