基于改进HHT的电能质量扰动检测方法*

2018-11-13胡雷陈湘波熊魁周峰岳长喜李智成

电测与仪表 2018年21期

胡雷，陈湘波，熊魁，周峰，岳长喜，李智成

(1.合肥工业大学电气与自动化工程学院，合肥 230009； 2.中国电力科学研究院武汉分院，武汉 430071)

0 引言

在工业生产和人民生活中，离不开许多新型电气设备的使用，在设备运行中，冲击性负荷会对电力系统的安全运行造成影响，从而引发电网中各种电能质量扰动问题。与此同时，随着电气化程度不断提高，用户对电能质量要求越来越高。由于电能质量扰动的现象是多种多样的，因此对其进行分析较困难，在实际应用中常见扰动包括谐波、电压暂降与短时间中断等，另外多种扰动同时发生的复合扰动现象也有可能存在[1]。相应的控制、补偿技术可以使电力系统中电能质量得到改善与提高，从而能够确保电网中电力设备安全经济的运行。准确地检测电能质量扰动信号，获取扰动源信息，是更好地采用控制、改善措施的首要前提，可以为电能质量的提高提供帮助。

在常见电能质量扰动信号中，非平稳信号占多数。针对非平稳信号，其时频分析方法有多种，传统方法包括短时傅里叶变换(STFT)[2]、小波分析[3]和S变换[4-5]等。STFT分析非平稳信号时，信号变化平缓时刻要求窗函数有较高的频率分辨率，而信号波形变化剧烈时刻则要求窗函数有较高的时间分辨率，STFT使用一固定的窗函数，时频分辨率也相应确定，不能同时兼顾时间和频率分辨率的要求。小波分析的时频分辨率是可变化的，在时域和频域同时具有良好的局部分析能力，但在分解过程中需要预先选择小波基函数，在信号分析过程中只能使用同一个小波基函数，易导致信号能量泄露，且小波基函数选择困难。S变换作为分析电能质量扰动信号的常用方法，具有良好的时域局部性能，但在非平稳信号分析过程中，其分解过程本质上也是非自适应处理，不具有自适应性。

希尔伯特-黄变换(HHT)可自适应地分析处理信号，特别适用于分析非平稳信号和突变信号[6-7]。与STFT、小波分析和S变换相比，HHT在经验模态分解(EMD)筛选过程中产生固有模态分量(IMF)，能够自适应产生“基”；完全摆脱了线性和平稳性约束，可在时域和频域同时达到很高的精度；在信号分析过程中瞬时频率采用求导得到，具有局部性质，而STFT的频率是全局性的，小波分析得到的频率是区域性的[8-9]。

传统HHT方法求取扰动信号的幅频参数波动程度较大，为减小其波动，提高检测准确性及定位能力，在传统HHT方法分析扰动信号的基础上，对得到各IMF的瞬时频率、幅值进行平滑处理。通过仿真，与传统HHT方法对比验证该方法的有效性和准确性。

1 HHT

HHT是1998年由Norden E. Huang等学者提出的一种分析非平稳信号的新方法，主要包括EMD和Hilbert变换两部分[10-11]。在信号分析过程中，EMD通过筛选可得到若干IMF和一个残余量，Hilbert变换分析每个IMF，从而获取对应的瞬时特征量[12]。

1.1 EMD算法

EMD基于信号的局部特征，将信号中不同尺度的波动或趋势依次分解开来，得到有限个IMF和一个残余量，原信号的局部特征可从各阶IMF中体现，残余量则反映了原信号的单调趋势。为了提取信号的局部时频特性，一般只需分析各阶IMF，忽略残余量。

IMF是由Norden E.Huang等学者在物理中瞬时频率有意义的基础上提出的，须满足以下2个条件：(1)在整个时间范围内，信号局部零交叉点与极值点数目需相差不能超过1个；(2)在任意时刻点，关于时间轴信号需局部对称，即通过信号的局部极大值点、极小值点确定包络线，其均值必须为零。

对任一信号y(t)进行EMD的具体步骤为：

(1)应用三次样条插值函数分别拟合原信号y(t)上所有极大值点和极小值点，形成上下包络线；求取上包络线与下包络线的均值曲线，记作m1(t)。

(2)将原信号y(t)减去均值包络曲线m1(t)，得到信号h1(t)：

h1(t)=y(t)-m1(t)

(1)

检测h1(t)是否满足IMF条件，若不满足，需要把h1(t)作为原信号，重复执行以上筛选过程，得到信号h11(t)：

h11(t)=h1(t)-m11(t)

(2)

执行k次，直至信号h1k(t)满足IMF条件，便得到第一阶IMF，用c1(t)表示第一阶IMF，记作：

c1(t)=h1k(t)

(3)

(3)将第一阶IMF信号c1(t)从原信号中分离出来，得第一阶剩余信号r1(t)。

r1(t)=y(t)-c1(t)

(4)

由于在r1(t)中仍含有其他低频分量，需要对r1(t)进行同样的分解。将r1(t)作为原信号重复以上筛选过程，便依次得到第n阶IMF和第n阶剩余信号。过程表示为：

(5)

直到rn(t)为单调函数时，停止筛选。由式(4)、式(5)得到：

(6)

EMD自适应地通过多次筛选将原信号逐个分解为有限个IMF信号ci(t)和单个残余量rn(t)。

1.2 Hilbert变换

对于IMF信号c(t)，定义它的Hilbert变换为：

(7)

定义IMF的解析信号为：

z(t)=c(t)+jH(c(t))=a(t)ejθ(t)

(8)

其中，a(t)为IMF的瞬时幅值，θ(t)为IMF的瞬时相位。

(9)

(10)

IMF的瞬时频率定义为：

(11)

在获得IMF后，对每个IMF就可以做Hilbert变换得到：

(12)

这里省略了残余量rn(t)；Re表示取实部，ai(t)和ωi(t)分别表示第i个IMF的幅值和频率。展开式(11)称为Hilbert谱，记作：

(13)

Hilbert谱描述了幅值ai(t)及频率ωi(t)随时间变化的关系，在时-频域上对信号幅值进行分析，Hilbert谱中线条颜色深浅反映信号幅值的大小，颜色越深，代表信号幅值越大。

2 改进HHT的方法

2.1 平滑处理

在传统HHT分析扰动信号的基础上，利用移动平均法对得到各IMF的瞬时频率、幅值进行平滑处理。移动平均法根据时间序列，逐项推移，依次计算包含一定项数的数据平均值。

设IMF的瞬时幅值序列为a1，a2，…，瞬时频率序列为ω1，ω2，…，移动平均法可表示为：

(14)

(15)

式中at、ωt为最新幅值、频率；at+1、ωt+1为下一期预测幅值、频率；N为移动步长，文中取30；由式(14)、式(15)可以看出每一新预测幅值、频率是对前一移动平均幅值、频率的修正，使幅频参数均值化，能有效地减小幅频参数的波动程度。

2.2 与传统HHT仿真对比

为了分析文中改进HHT方法应用于电能质量扰动信号的有效性及准确性，文中应用Matlab R2014a仿真环境，以电力系统中常见谐波信号为例，分别采用传统和改进HHT方法对信号进行时频分析，现构造一谐波信号，其表达式为：

y(t)=220cos(100πt)+80cos(300πt)+

40cos(700πt)

(16)

信号基波频率为50 Hz，幅值220 V，信号中含幅值80 V的3次谐波和40 V的7次谐波；信号采样频率为1 500 Hz，时间长度为1 s。分别采用传统和改进HHT方法对该信号进行时频分析，得到图1、图2中Hilbert谱和幅值特性曲线。

图1 传统HHT方法的分析结果

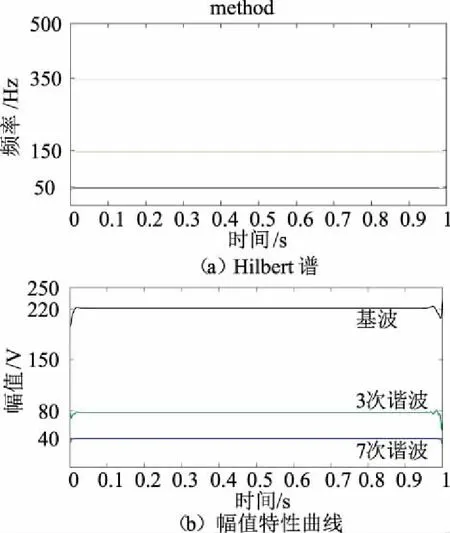
图2 文中改进HHT方法的分析结果

图1为传统HHT方法的谐波检测结果，可以看出该方法求取谐波信号的幅值特性曲线和Hilbert谱波动程度较大，在高频区的7次谐波频率波动标准差可达20.6 Hz，导致Hilbert谱中对应线条波动太大，无法清楚反映谐波频率，幅值波动标准差可达4.5 V，对比图2可知，文中改进HHT检测谐波频率波动标准差在0.5 Hz以内，幅值波动标准差在0.3 V以内，可有效减小幅频参数的波动程度，实现谐波频率及幅值的精确检测。

通过与传统HHT分析对比，验证文中改进HHT方法的有效性，在以下仿真中，均采用该方法分析扰动信号，并进行相应误差分析。

2.3 电能质量扰动检测方法流程

提出一种基于改进HHT的电能质量扰动检测方法，对于电压暂降与短时间中断信号，可视作调幅信号，满足IMF的2个条件，故为同类信号，可直接进行Hilbert变换分析。具体步骤如下：

(1)对电压暂降与短时间中断信号，可直接进行Hilbert变换，计算各IMF的瞬时频率和幅值；

(2)对谐波信号和复合扰动信号，进行EMD得到若干IMF后，对各个IMF进行Hilbert变换，从而获得瞬时幅频特征参数；

(3)利用移动平均法对瞬时频率和幅值进行平滑处理，将各个IMF表示在联合的时频域中，得到原信号的Hilbert谱，并同时绘制幅值特性曲线；

(4)从Hilbert谱和幅值特性曲线中提取有效的特征量，实现电能质量扰动信号的时频特性精确检测。

3 仿真结果与分析

在上述传统与改进HHT方法仿真分析对比结果的基础上，对电网中其他常见电能质量扰动信号进行仿真分析，分别对电压暂降与短时间中断信号、谐波信号和复合扰动信号进行时频分析与计算。

3.1 电压暂降与短时间中断信号仿真分析

对某一相电压方均根值为220 V、频率50 Hz的三相系统进行仿真研究，设某一相的电压在0.35 s～0.55 s之间发生了电压暂降，暂降幅值为140 V，信号波形如图3(a)所示，信号表达式为：

y(t)=(220-140 (u(t-0.35)-

u(t-0.55))cos(100πt)

(17)

式中u(t)为单位阶跃信号，信号采样频率1 000 Hz，时间长度为1 s。对该信号进行分析，得到图3(b)～图3(c)。

图3电压暂降信号检测

由图3(b)～图3(c)可知，检测得出信号电压暂降起始时间为0.351 s、终止时间为0.551 s，电压暂降幅值为139.97 V。

现构造一电压中断信号，设某一相的电压在0.3 s～0.5 s之间短时间中断，信号波形如图4(a)所示，信号表达式为：

y(t)=(220-220 (u(t-0.3)-u(t-0.5))cos(100πt)

(18)

信号采样频率1 000 Hz，时间长度为1 s。仿真分析得到图4(b)～图4(c)。

图4 电压中断信号检测

由图4(b)～图4(c)可知，检测得出信号电压短时间中断起始时间为0.304 s、终止时间为0.504 s。

表1给出了文中改进HHT方法检测电压暂降与短时间中断扰动信号起止时刻的定位能力，表中t1、t2分别表示扰动起始时刻、终止时刻，u表示电压暂降幅值。由表1可知，电压暂降扰动起止时刻检测精度优于0.28%，暂降幅值检测精度可达0.02%，故文中方法可以精确检测电压暂降起止时刻及幅值；电压中断扰动起止时刻检测精度均在1.5%以内，精度有待提高，但已基本满足工程应用的需求。

表1 电压暂降与短时间中断信号检测误差分析

3.2 谐波信号仿真分析

在电网中可能存在扰动突变谐波信号，现设一突变谐波信号，信号基波频率为50 Hz，在0.4 s处谐波突变，该信号波形如图5(a)所示，信号表达式为：

(19)

信号采样频率为1 000 Hz，时间长度为1 s。通过改进HHT方法，对该谐波信号进行EMD分解，得到如图5(b)所示的IMF分量图。从图5(b)可知，IMF1为谐波信号，IMF2为基波信号。再经分析计算，得到图5(c)～图5(d)。

图5 谐波信号检测

由图5(c)～图5(d)，可知信号中基波频率为50 Hz，且含有突变谐波，检测出谐波频率分别为150.4 Hz和349.6 Hz, 3次谐波对应的幅值为80.15 V，7次谐波对应的幅值为40.18 V，而且可以清楚的看到0.401 s处为谐波信号的分界点。由此可知，改进HHT方法具有相对较高的幅频分辨率和时间区分特性。

表2给出了文中改进HHT方法检测突变谐波信号幅值、频率及突变时刻的误差分析情况，表中f表示谐波频率，u表示谐波幅值，t表示突变时刻。从表2可知，谐波信号频率检测精度优于0.27%，幅值检测精度优于0.45%，突变时刻检测精度可达0.25%，改进HHT方法可精确检测突变谐波信号频率、幅值及突变时刻。

表2 谐波信号检测误差分析

3.3 复合电能质量扰动分析

对于单一电能质量扰动的检测，发现算法具有很好的效果。除了单一扰动，实际电网中可能存在复合电能质量扰动，现构造电压暂降与谐波复合扰动信号进行仿真分析，信号包含基波和5次谐波，在时间0.5 s～0.7 s内发生电压暂降，暂降幅值为135 V，该信号波形如图6(a)所示。信号表达式为：

y(t)=220cos(100πt)+80cos(500πt)-

135cos(100πt)[u(t-0.5)-u(t-0.7)]

(20)

对该复合扰动信号进行EMD分解，得到如图6(b)所示的IMF分量图。IMF1分量图为谐波信号波形，IMF2分量图为基波信号随时间变化的波形。

对各IMF进行Hilbert变换，分析得到图6(c)～图6(d)。

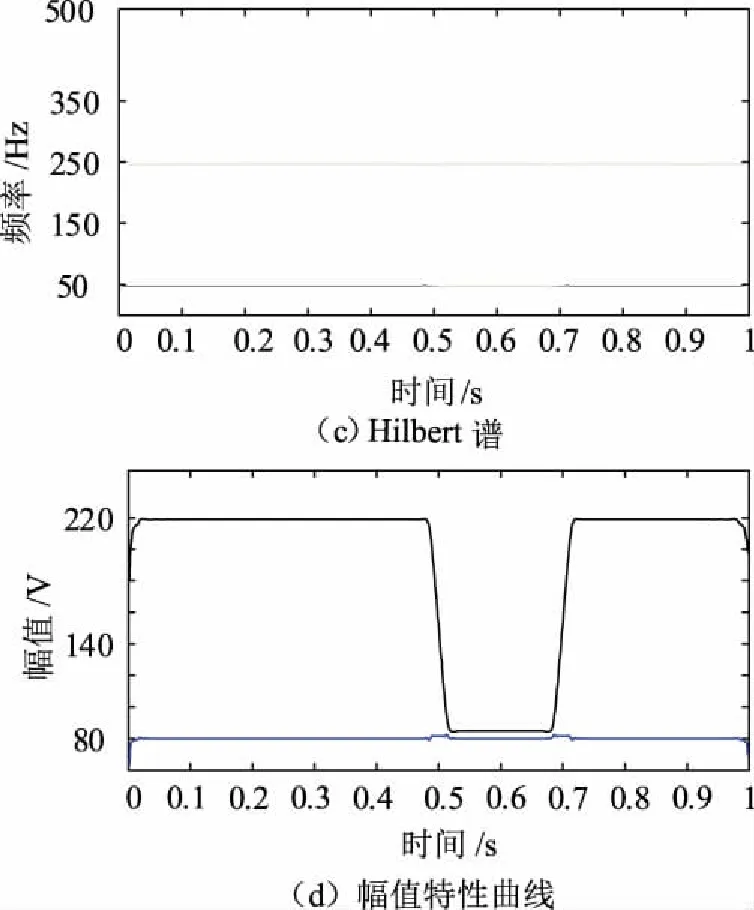
图6 复合扰动信号检测

从图6(c)～图6(d)可知，信号包含基波和频率为250 Hz谐波，基波幅值为219.2 V，谐波幅值为79.99 V，电压暂降的起始时间为0.501 s，终止时间为0.701 s,电压暂降幅值为134.35 V。

表3给出了文中改进HHT方法检测复合扰动信号的误差分析，表中t1、t2分别表示扰动起始时刻、终止时刻，u1表示电压暂降幅值，f表示谐波频率，u2表示谐波幅值。从表3可知，改进HHT方法同样适用于检测复合电能质量扰动，检测电压暂降起止时刻精度优于0.2%，暂降幅值精度为0.48%，可精确检测谐波幅值、频率。