基于聚类经验模态分解和差分熵的输电线路故障测距研究*

2018-11-13张成王昕郑益慧李立学

电测与仪表 2018年21期

张成，王昕，郑益慧，李立学

(上海交通大学电工与电子技术中心, 上海 200240)

0 引言

高压输电线路作为社会经济高速发展的动脉，需要面对故障多发的问题，一旦处理不及时，会影响整个电网稳定性。因此研究输电线路的故障测距，在线路故障发生后，排除信号噪声的干扰，进行快速、准确的故障定位，对经济发展和社会稳定具有重要意义。

当输电线路发生故障时，暂态行波会出现包含丰富故障信息的波头，为故障信息的提取和故障位置的确定提供了基础[1-2]。行波法测距易受电流信号噪声影响，为此需要去除原始信号中的噪声，获得有效的行波信号。小波变换 (Wavelet Transform，WT)[3]在去噪过程中对非奇异信号具有良好的检测效果，但对于不同信号，最优的分解尺度和基函数选择难度较大，在实际使用中去噪效果不理想。希尔伯特-黄变换(Hilbert-Huang Transform，HHT)[5-6]通过经验模态分解(Empirical Mode Decomposition，EMD)将信号分解为一组固有模态函数(IMF)，利用希尔伯特变换(Hilbert Transform，HT)计算各分量的瞬时频谱，不需要选择分解尺度和基函数，但EMD算法容易造成模态混叠现象，去噪不充分，导致故障测距具有不小的误差。局域模态分解(Local Mean Decomposition，LMD)[7]方法在去噪过程中采用平滑处理的方法形成局部均值函数和局域包络函数，可避免EMD分解采用三次样条函数时产生的过包络、欠包络现象，提高去噪效果。但LMD分解需要进行多次迭代，相比于EMD分解计算量较大，是其主要的局限性。

行波法的关键是确定行波波头到达监测点的精确时间。文献[8]利用HHT得到高频信号的时间-频率关系，根据突变信号对应的发生和结束时刻，确定故障行波波头，但该方法易受HHT端点效应的影响。文献[9]利用韦格纳维尔分布获得行波的瞬时能量谱曲线，通过电压峰值确定行波波头达到时刻。由于输电线路电压测量精度不高，该方法的实际效果有待验证。文献[10]利用每个数据点附近的熵值变化来判断信号较正常情况是否发突变，根据熵值最大点确定突变时刻。由于获得的是不同时间段信息熵的变化情况，据此求得的突变时刻精度不高。

针对输电线路故障测距存在的噪声影响和时间精度问题，提出了基于聚类经验模态分解和差分熵的输电线路故障测距方法。首先利用改进的差分熵DE(Difference Entropy)信号处理方法对电流信号进行熵值计算，通过与正常电流熵值的对比，判别突变电流。然后针对发生突变的故障电流，采用EEMD(Ensemble Empirical Mode Decomposition)分解法进行处理，有效去除故障信号中的噪声，避免模态混叠，获得准确反映故障信息的IMF分量。随后对分量实行差分熵方法中的差分分析，将电流的变化幅度进行有效量化，建立每个信号点的变化幅度与时间的对应关系，获取故障初始行波到达每个监测点的准确时间。最后利用行波双端法，实现输电线路的故障测距。通过不同故障类型、故障距离、故障接地电阻的仿真结果分析表明，该方法能够更好地检测故障行波的波头，具有较高的故障定位精度。

1 EEMD分解

1.1 EEMD分解基本原理

EEMD是针对EMD方法的不足,提出的一种噪声辅助数据去噪方法。EMD方法在进行有效去噪时，需要满足信号极值点均匀分布的条件，否则会出现模态混叠现象。为了解决该问题，EEMD分解利用了白噪声频谱均匀分布的特性，对信号添加白噪声，将不同时间尺度的信号分布到合适的参考尺度上。利用零均值噪声的特性，采用足够的测试量并取全体均值，消除噪声，从而避免了模态混叠，可以获取有效的IMF分量。

EEMD分解的步骤如下：

(1)向信号数据加入正态分布的白噪声；

(2)将加入白噪声的信号进行EMD分解得到多个IMF分量；

(3)重复步骤(1)、步骤(2)加入新的白噪声进行分解；

(4)将每次分解所得的IMF分量取均值作为最终结果。

1.2 EMD分解与EEMD分解效果比较

为比较EMD分解和EEMD分解的效果，将低频正弦信号加入20 dB的加性高斯白噪声。图1为添加噪声之后的原始信号。

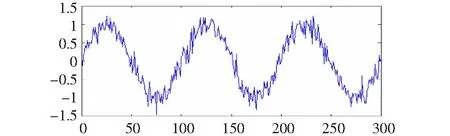
图1 原始信号

这里采用函数EEMD(Y,Nstd,NE)实现信号去噪。其中Y为输入数据，Nstd为高斯白噪声的标准差，具体数值根据噪声干扰大小而定，一般设置为0.01～0.4。NE是用来设置添加噪声的次数，通常取50或100。

对图1中的信号进行EMD和EEMD分解，可得两组IMF分量，两种分解方法的前三个IMF分量分别如图2、图3所示。

通过图2、图3对比可以看出，EMD分解的低频分量混杂较为明显，而EEMD的分解效果更为彻底，可以更好的将高频噪声信号和低频信号进行分离。在确定故障行波波头位置时，主要提取集中反映信号突变信息的IMF1分量进行研究。

图2 EMD分解

图3 EEMD分解

2 差分熵

2.1 差分熵基本原理

熵的概念最早是用来表示热力学中能量在空间中分布的均匀程度，能量分布的均匀程度越高，熵值越大[14]。信息论创始人香农提出了信息熵的概念，用熵表示信息量的丰富程度，用熵值的大小来度量信息的不确定度[15]。对于连续变量，信息熵H的定义如式(1)所示，其中f(x)表示概率密度。

(1)

对于离散事件，事件的发生由一系列独立的结果构成，假设每个结果发生的概率为p(i)(i=1,2,...N)，事件的信息熵可表示为：

(2)

文献[16]在信息熵的基础上提出了差分熵的概念，但上述差分熵信号处理方法主要通过每个信号点附近区间的变化程度，来研究信号整体的变化情况，无法建立信号曲线上某一点幅值的变化情况与时间的精确对应关系。特别是在信号区间的起点和终点附近，由于无法满足相应的时间尺度，区间两端的信息变化特征将会丢失，降低了差分熵的准确性。针对上述问题，对传统的差分熵信号处理方法进行了改进，假设经过噪声去除的信号为g(x)，为了表示信号在突变处的信息丰富度，差分熵表示如下：

D(n)=g(n+1)-g(n),n=1，2，…N-1

(3)

(4)

(5)

通过D(n)的差分计算获得信号各点的变化幅度，利用p(n)得到各点相对整体信号的变化权重，结合H(n)对各点变化权重进行熵值求和，获得反应信号整体变化程度的差分熵，用来区分正常信号与异常信号。其中式(3)、式(4)完成了每个信号点变化程度的数值量化，能够有效突出信号突变点的相对位置，在此定义上述过程为差分分析。

2.2 差分熵对正弦信号的分析

根据上述改进的差分熵信号处理方法的定义，通过式(5)可知在信号稳定时信号差分熵为一固定值，当信号发生突变时，信号差分熵值将增加。通过式(3)、式(4)画出每个数据点的差分分析情况，可以确定信号发生突变的具体位置。文中将对正常信号和异常信号采用上述方法进行对比分析，证明差分熵用于信息突变识别的可行性。

设置理想的正弦信号如式(6)所示：

(6)

对信号进行差分熵计算，可得信号熵值为H=8.227 71。如图4所示，信号的差分分析值呈周期性变化。为突出信号异常后的变化情况，对差分分析结果取0.007作为阈值，得到差分值结果恒为零，认为信号未发生突变现象。

设置异常信号如式(7)所示：

(7)

在相同的低频信号上添加异常高频信号，计算其差分熵为H=8.313 4。与正常信号差分熵比较可知，加入突变信号后差分熵增大，可以用来判断信号异常。再对该异常信号进行差分分析，结果如图5所示。与图4比较可知，在阈值同为0.007的条件下，添加异常信号后的差分分析值不恒为零，因此可以证明信号在相同时间内发生了突变。且首个波头的横坐标与高频信号的加入时间相对应，证明差分分析能够明确信号突变点的相对位置，建立信号突变点与时间的准确对应关系。

图5 异常差分熵分析

3 基于EEMD-DE方法的故障定位应用

电能在输电线路中以波的形式进行传播，当故障行波达到检测点时，电流信号会发生明显的波动，信号的信息丰富度会明显增加，差分熵相较于正常时间段也会显著增大。文中的测距方法以双端法为基础，具体步骤如下：

(1)从故障线路M、N各相测得电流信号ima、imb、imc和ina、inb、inc；

(2)对电流信号进行Clark变换，进行去耦合，得到线模分量iβm、iβn；

(3)选取线模分量进行差分熵Hm、Hn计算，根据差分熵判断电流是否发生突变；

(4)将突变的电流信号进行EEMD分解，得到集中故障信息的IMF1m、IMF1n分量；

(5)对IMF1m、IMF1n进行差分分析，记录M、N两端瞬时电流突变的时间点t1、t2；

(6)通过线路相关参数确定行波传递速度v和线路长度l，根据双端法故障定位公式确定故障点距离M端的位置为s。

(8)

4 仿真验证

为验证所提方法在故障测距中的有效性，用PSCAD软件搭建的220 kV输电线路模型如图6所示。仿真中的采样频率取1 MHz，对应一秒有106个点，通过突变点与其他点的相对位置确定行波到达时间。系统M端电压源电压为220∠60°kV，N端电压源电压取220∠90°kV，均为理想电压源。输电线路长度取100 km，在距离M端80 km处发生单相接地故障，接地电阻为50 Ω，仿真运行时间为0.3 s，在0.153 s发生故障。输电线路的工频参数如表1所示。M端故障电流波形如图7所示。

图6 220 kV 输电系统仿真模型

图7 M端故障电流

参数类型R/(Ω/km)L/(H/km)C/(F/km)正序参数0.3311.326e-30.008 7e-6零序参数0.481 74.595e-30.004 8e-6

行波波速在线测量约为2.941 8×108m/s，在提取仿真模型的电流数据后，利用Matlab对数据进行EEMD分解，如图8所示。求出差分熵，并利用差分分析结构确定M、N测量点接收到故障行波的时刻。测得正常运行时的差分熵为10.281 9，故障后差分熵Hm、Hn分别为11.258 8、11.146 6。M端经过去阈值的差分分析结果如图9所示，由图可得信号突变点的变化程度相较其他点区别明显，M端的故障行波波头在所有采样点中的分布位置为153 271，同理可得N端故障行波波头的分布位置为153 068，根据式(8)计算可得故障点距离M端测量点为79.86 km,相对误差为0.175%。

图8 M端EEMD分解

图9 M端差分分析

为验证不同故障距离对测距结果的影响，在图6所示系统的基础上，分别设故障距离为10 km、30 km、50 km、75 km，对单相接地故障进行仿真，结果如表2所示。

表2的仿真结果说明，对于不同的故障距离，该方法都能获得较好的测距效果，即使在距离线路两端监测点最远的中点处，定位误差依然在300 m的安全范围内。

为验证不同接地电阻对测距结果的影响，在图6所示系统的基础上，分别设接地电阻为1 Ω、10 Ω、100 Ω、400 Ω进行仿真分析，故障时刻取0.153 s，故障选在离M端80 km处，测距结果如表3所示。

表2 故障距离对测距结果的影响

表3 接地电阻对测距结果的影响

由表3的仿真结果看出，在接地电阻达到400 Ω时，定位精度仍能满足要求。

为验证不同故障类型对测距效果的影响，在图6所示系统的基础上，分别取A相接地、AB相短接、AB相短路接地、ABC三相短接这四种常见故障进行仿真分析，故障时刻取0.153 s，故障选在距离M端80 km处，测距结果如表4所示。

表4 接故障类型对测距结果的影响

表4列出的测距结果显示，对于输电线路常见的不同故障类型，该方法的定位误差无明显差异，且定位精度依然保持在300 m的安全范围内。

为证明该故障测距算法的优越性，在图6所示系统的基础上，分别设故障距离为30 km、75 km，对单相接地故障分别采用小波变换、HHT、LMD等常见故障测距算法和所提算法的测距结果进行对比，测距结果如表5所示。

表5 不同定位算法的测距结果对比

表5列出的测距结果显示，相较于传统的故障测距方法，该方法的测距可靠性更高，精度更能满足实际安全范围。

综合以上数据分析结果可以看出，该测距方法对于不同的故障距离、接地电阻、故障类型均能取得较好的测距效果，且优于传统的测距方法。

为验证上述基于聚类经验模型分解和差分熵的输电线路故障测距算法在实际场景中的有效性，设计了基于上述算法的故障检测单元，并在某公司某线路上完成安装，装置和安装现场如图10所示。在实际挂网期间，在距离故障检测单元35.6 km处发生线路故障，而单元球返回数据显示故障在距其35.8 km处，证明了该算法在实际应用中的可行性。