一种基于电压静态稳定性的电力系统自复性指标

章熙，贺先强，覃海，张通，郑杰辉，李志刚

(1.贵州电网有限责任公司 电力调度控制中心，贵阳 550002； 2.华南理工大学 电力学院，广州 510640)

0 引 言

随着电网的发展，电网的规模逐渐扩大、复杂程度逐渐加深、负荷逐渐增多，这对电力系统的安全稳定运行提出了更加严格的要求。其中，电力系统的运行稳定是其正常运行中一个必须得到保障的环节，为了保障电网的正常运行，对电网某些与电压相关的指标进行检测是不可省略的。

由针对系统静态电压稳定程度的评价方法产生的各类单一指标能够直观地体现系统是否在合理的运行范围内，并一定程度上反映系统的稳定程度，即系统当前的运行状态距离电压崩溃状态的距离[1]。常用于表现系统电压稳定的指标包括：(1)负荷裕度指标，即系统当前状态某一节点的功率到节点极限功率(系统崩溃临界状态的负荷)的距离[2]，通常包括有功功率指标、无功功率指标等，其变化趋势一般通过P-V曲线、Q-V曲线表示。该指标随着系统的负荷水平变化呈现线性变化，直观地体现了电压的稳定水平；(2)灵敏度指标，即通过系统计算方程中不同变量的微分关系来体现系统的电压是否在合理范围[3-4]，常用的灵敏度指标包括了负荷节点电压幅值对该节点有功功率、无功功率的灵敏度等，当系统接近临界状态时，负荷的少量变化会导致节点电压的大幅波动，即灵敏度的取值呈非线性快速增长，由此实现对系统电压稳定的判断功能；(3)雅克比矩阵特征值、奇异值指标，当系统崩溃时，潮流计算方程的雅克比矩阵奇异，故矩阵接近奇异的程度也可以用来识别系统是否运行在正常电压范围[5]；(4)L指标，该指标通过建立在潮流方程基础上的等式构建，体现了不同节点之间的电压接近程度，从而反映系统现在的运行点与功率极限之间的距离[6]。除此之外，通过对系统潮流的是否多解的状态进行分析，也可以构造电力系统的自复性指标[7]。

以上的各类指标在电网的优化调度中，通常会作为目标函数的一部分，或者被纳入约束[8-10]。此时，电压的静态稳定常通过单一类型的指标进行反映。这些改善或保证电压稳定水平的方式比较直观，但也存在信息量不全面的问题。例如：系统的负荷裕度指标是在确定系统负荷增长方式的前提下进行计算的，然而系统的负荷变化方式不确定，只能做到大概估计；同时该指标的计算量大、计算时间长。灵敏度指标仅体现了某两种物理量之间的关系，如节点电压幅值对节点无功功率的灵敏度无法体现系统有功功率对电压的影响，不同节点的负荷水平不同，在灵敏度同样时，节点负荷对该节点电压、系统整体电压的影响程度也不一样。故常用的电力系统静态电压稳定指标，只能从某些特定角度对系统的稳定性进行判定，仍有一定局限性。

提出了一种综合的电力系统自复性指标，该指标结合了反映系统整体的雅克比矩阵最小特征值，以及节点的L指标，既考虑了系统整体运行的稳定性，又考虑了系统各节点的电压稳定程度，对于系统负荷变化、优化前后的状态可以进行有效的评估。

1 电力系统运行稳定的评判方法

所使用的自复性指标的定义建立在系统静态电压稳定性的概念上，是指电力系统在某一特定运行状态下的稳定程度。自复性指标的计算包括了两类独立的具体指标：降阶雅克比矩阵最小特征值和节点L指标。

1.1 降阶雅克比矩阵最小特征值评价方法

当系统处于准静态的状态时，随着负荷的逐渐提高，系统电压逐渐下降，在电压失稳的极限点附近，潮流方程雅克比矩阵变得奇异。若对雅克比矩阵进行特征值分解，可以发现，随着电压的下降，雅克比矩阵的最小特征值逐渐接近零。故雅克比矩阵的奇异性可以作为系统是否失稳的判据，而雅克比矩阵的最小特征值的大小则可以代表系统当前运行状态的稳定程度，即当前运行电压的稳定裕度。对潮流方程的雅克比矩阵进行特征值分解，可得：

(1)

式中J为潮流方程的雅克比矩阵；X和Y分别是右特征值矢量与左特征值矢量，由xi和yi组成；Λ则为特征值对角矩阵，其对角元素μi为矩阵的特征值[3]。

文中为了减少特征值分解的计算负担，利用潮流计算方程构建降阶的雅克比矩阵，并进行特征值分解。电力系统潮流方程可表示为：

(2)

式中JPθ，JPV，JQθ，JQV即为有功功率、无功功率对于电压幅值、电压相角的分块矩阵。假设有功功率变化ΔP为零，则可得：

(3)

降阶雅克比矩阵计算公式即为：

(4)

降阶雅克比矩阵与系统潮流方程计算所使用的雅克比矩阵奇异性变化趋势一致，可以通过计算JR来识别系统电压是否仍在正常范围内[11]：对降阶雅克比矩阵进行特征值分解，最小的特征值为零时，雅克比矩阵奇异，电力系统崩溃。对负荷节点集合TL内的所有节点的特征值进行比较，最小特征值则用来表示电压稳定性的指标Ieigen(V)：

(5)

当电力系统稳定程度降低时，此时系统的雅克比矩阵也会越来越接近奇异。即降阶雅克比矩阵的最小特征值越小，系统越不稳定；降阶雅克比矩阵最小特征值越大，系统越稳定。特征值指标是一种“全局型”稳定指标，该指标并非对某一节点的的运行情况进行计算，而是通过对系统整体的潮流方程求解情况体现系统的稳定性。

1.2 L指标评价方法

L指标最初由两节点系统导出，其判据在于：当系统的电压稳定时，系统的潮流方程由高压解、低压解组成，而当系统即将崩溃时，潮流方程只有一个解；而当系统电压已经崩溃时，无解。通过推导节点的电压公式并进行求解，可以找出系统电压稳定的必要条件，并以此作为判据。

对于多节点系统，节点方程通常可以用以下形式表示：

I=YV

(6)

式中Y是系统的节点导纳矩阵；I和V则分别代表了电流、电压矢量。对于节点数大于2的系统，该方法把系统全部节点分为两类，即发电机节点TG(含PV节点与平衡节点)与全部PQ节点集合TL，其中发电机节点的电压幅值恒定。节点方程可以扩展为以下形式：

(7)

(8)

对于多节点系统中的某个负荷节点j，在对其电压进行求解时，若潮流方程有两个解，则该节点的L指标的取值范围为(0,1);当系统处于临界状态，仅有一解时，L指标的值恰好为1；当潮流方程无解时，L指标的值大于1。即L指标取值越小，系统越稳定；故L指标的取值对于节点电压的稳定性具有指示作用。对于系统整体，各节点中L指标取值最大的节点即为最脆弱节点，取该节点的L指标取值代表系统整体的稳定性，即为：

(9)

系统L指标对系统所有负荷节点的稳定情况分别进行评估，并选出最薄弱的节点的L指标作为系统的最终指标，即系统中最薄弱节点的电压稳定情况决定了系统的电压稳定程度。不同于由系统整体稳定水平决定的最小特征值指标，L指标的大小是由系统某个节点决定的。

2 自复性指标的计算方法

电力系统的自复性的计算过程包括了独立指标的计算、指标的预处理以及自复性指标的综合计算。

2.1 指标的预处理

电力系统自复性指标包含了两种不同的电压稳定性指标，最小特征值指标取值范围为(0,+∞)，当系统稳定性逐步下降时，最小特征值指标也逐渐减小；对于稳定运行的电力系统，L指标取值范围在0到1之间，系统稳定性下降时L指标的值逐渐增大。为了整合两种具有不同的取值范围和变化趋势的指标，需要对这两类指标进行预处理。在进行预处理之前，设定系统的稳定程度原告，系统的自复性指标取值越大。

对于降阶雅克比矩阵特征值，系统节点数量影响特征值的大小，即系统规模越大，其雅克比矩阵的特征值整体取值范围越小。为了方便计算，并保证特征值指标的数量级、变化趋势L指标相同，应构造以特征值指标为变量的函数来代表最小特征值指标：

(10)

对于系统的L指标，其取值范围与自复性指标相同，故仅需要统一指标取值的变化方向：

(11)

2.2 系统自复性指标的构建

自复性指标既包括了系统的电压稳定裕度，又包含了系统各节点的电压稳定程度。对上述两类指标进行加权，可以得到电压自复性综合指标I(V)，其计算公式如下：

(12)

式中ω1与ω2则为与两类指标相对应的权重，权重和为1。由于最小特征值指标代表了系统整体的电压稳定性，L指标则代表了系统节点的最低电压稳定程度，对系统整体与个别节点的重视程度不同，两类指标的权重便会不同。权重的选择通常视实际运行中的要求而定。

已知，经过标准化处理后的降阶雅克比矩阵最小特征值指标与L指标的取值上限均为1，且两类指标随着电压稳定水平的上升而增加，故系统在稳定运行时，电压自复性指标的取值范围在[0，1]之间，电压稳定性水平提高时，该指标取值增加；电压稳定性水平降低时，该指标取值降低。指标的计算过程如图1所示。

图1 电压自复性指标计算流程图

3 仿真研究

3.1 IEEE 30节点系统

在仿真中，采用IEEE 30节点系统，该系统含有6个发电机节点与41条支路。在基态情况下，系统的运行工况与最初的设置一致，通过潮流计算得到L指标、降阶雅克比最小特征值指标：系统的L指标取值为0.143 7，来自于节点30；系统降阶雅克比矩阵最小特征值则为0.509 8。当权重分别设为0.5时，系统此时的自复性指标得分为0.627 8。

当系统的负荷水平改变时，系统电压的稳定水平发生变化。假设系统全部负荷节点的有功功率、无功功率均以同一倍数进行改变，此时降阶雅克比矩阵最小特征值、系统L指标的变化如图2、图3所示。

图2 IEEE 30点电力系统降阶雅克比矩阵最小特征值变化

图3 IEEE 30节点电力系统L指标变化趋势

对以上两类指标进行数据预处理、加权求和后，可以得到综合的电力系统稳定性指标(权重各设为0.5)，如图4所示。可以看到，随着系统负荷水平逐渐增长，降阶雅克比矩阵的最小特征值逐渐变小，而系统L指标逐渐增大。此时，系统的电压自复性指标取值逐渐降低，这意味着负荷的增加使电力系统的稳定程度逐渐减小。

图4 IEEE 30节点电力系统自复性指标变化趋势

3.2 某实际电网

在仿真中，采用某实际电网系统，该模型共有1 209个节点，95台发电机，1 563条输电线路。在基态工况下，系统的L指标取值为0.424 9，来自于节点661；系统降阶雅克比矩阵最小特征值则为0.388 2。当权重各设置为0.5时，系统自复性指标得分为 0.551 61。

当系统的负荷水平改变时，系统电压的稳定水平发生变化。令各负荷节点处负荷功率因数不变，功率逐渐增长，系统的最小特征值指标、L指标及电压自复性指标(权重均设为0.5)如图5～图7所示。可以看到，当系统逐渐趋于失稳状态时，雅克比矩阵最小特征值逐渐减小，L指标逐渐增大，自复性指标逐渐减小，即系统运行稳定程度逐渐降低，说明电力系统自复性能够反映系统的静态电压稳定水平，从而体现系统运行的稳定性。

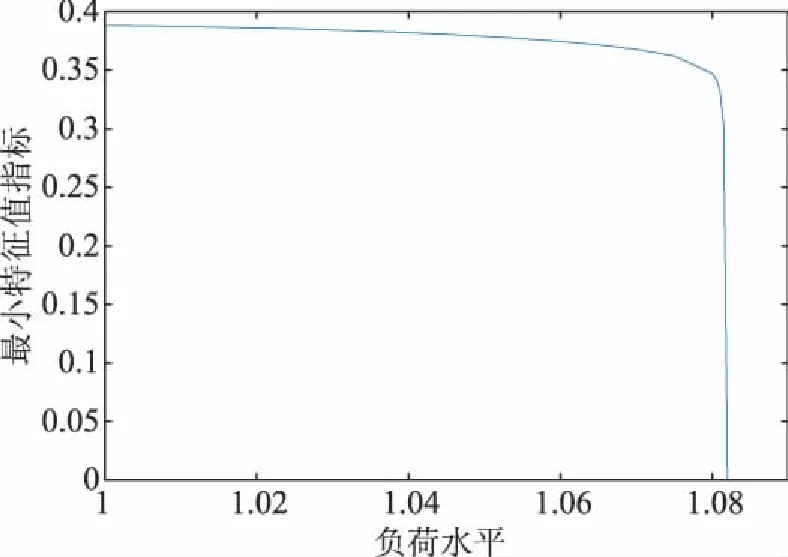
图5 某实际电网降阶雅克比矩阵最小特征值指标变化趋势

图6 某实际电网L指标变化趋势

图7 某实际电网综合电压稳定指标变化趋势

4 结束语

提出了一种基于静态电压稳定性的系统自复性指标，该方法结合了潮流方程降阶雅克比矩阵的最小特征值指标与L指标，反映了系统整体稳定性与各节点电压稳定程度。采用了IEEE 30节点系统以及某一实际电网模型，使用该方法对不同负荷水平下的系统电压稳定性进行了计算，仿真结果表明自复性指标能够直观地体现系统电压稳定性，并能够协助运行人员观察不同运行状态下系统电压稳定程度的变化。