基于GA的二自由度PID在火电机组的应用

吴延凯， 张 伟

(上海理工大学 光电信息与计算机工程学院，上海 200093)

0 引言

随着社会的发展进步，PID的参数调节方法同样也在不断地进步。1942年，Ziegler和Nichols运用一阶惯性加延迟对象的PID控制器参数整定，也即Z-N方法，这为PID控制器的进步奠定了基础[1]。1970年，Astrom和Hagglund在临界比例度原理上,结合ISTE标准,提出使用基于临界信息的相幅裕度设置参数，并给出了参数整定公式，解决了Z-N法整定时间长、临界稳定的缺点[2]。随后，针对运用Z-N法得到的PID参数在实际控制中往往会引起系统响应的过度超调、过度振荡等不符合工艺要求的结果，C.C.Hang在原始Z-N法的基础上,在Z-N法中增加了设定值权值和积分时间修正系数，很好地解决了这些缺点[3]。2011年，Karunagaran等人创建了一种基于二自由度并行控制结构的PID控制器，改善了单自由度PID控制器不能同时兼顾目标值跟踪特性及外扰动抑制特性的缺点[4]。

目前，火电厂的火电机组控制回路正向着大容量，高参数的方向发展，对控制系统的可靠性和精度提出了更为严格的要求[5]。尤其是对锅炉的主蒸汽温度的控制上，显示出了更为严格的要求，因为主汽温的值严重影响着火电机组能否正常的运行[6]。在此环境下，本文提出了一种基于遗传算法的二自由度PID控制器的多参数智能调节方法。保证主汽温维持平衡，以确保火电厂的火电机组控制回路更有效的运转。针对PID的多目标优化问题，采用自适应遗传算法对二自由度PID控制器的参数进行调节与优化。由控制系统的性能需求，对每一项指标值进行适当的加权，并实时优化。最终通过仿真证明，基于遗传算法改进的二自由度PID要优于文献[7]中的二自由度并行控制结构PID，在各项性能指标值、目标值跟踪特性及抗扰动特性上有着极大程度地改善，能够更好地应用于主汽温的控制上。

1 二自由度PID控制器原理

在工业生产中，由于PID控制器具有良好的控制性能，故被广泛的应用。尤其是用在生产过程中干扰作用强，被控制对象的极易变化，并且对控制的需求要求很高的地方。一般情况下，PID控制器将比例、积分及微分调节三者组合在一起，各自发挥出各自的长处，共同对被控对象进行良好的控制[8]。

在常规的单自由度PID控制器中，它仅有唯一的一个PID可以进行调节。这样，就会出现一个问题：控制系统不能同时使得系统的抑制扰动的能力和目标值的追踪同步的到达最佳控制效果。当利用抗干扰性质调整PID的参数时，就不能保证目标值的追踪效果是好的；相应的，当利用目标值的追踪性质调整PID的参数时，会让系统在抑制扰动方面的性能下降[9]。对待这一问题，只能采用一种两者同时兼顾的方法来进行PID控制器参数的调节。因此，二自由度的PID控制器就应运而生，并在实际应用中取得了良好的效果[10]。与一般的单自由度PID相比较，二自由度的PID大大提高了目标值的跟踪特性和抑制干扰的特性。如图1所示为文献[7]中提出的一种二自由度并行控制结构PID控制器的原理框图。

图1 二自由度并行控制结构PID控制器原理图

其中，r(t)为系统输入，d(t)为扰动输入，u1(t)为PD输出，u2(t)为PID输出，u(t)为两个控制器输出的叠加，y(t)为系统输出。

对于PD(Gc1)，主要调节跟踪特性，其控制方程可表示为：

Gc1(s)=Kc1(1+Td1s)

(1)

对于PID(Gc2)，主要调节抗扰动特性，其表达式为：

(2)

该二自由度并行控制结构的闭环输出表达式为：

(3)

在二自由度PID的参数调整过程中，采取：Gp=Gm，则可表示为：

(4)

在式(1)和(2)中，Kc1和Kc2为控制器增益，Td1和Td2为微分时间常数，Ti2为积分时间常数。比例调节的过程简单迅速，并且参数的调节也很方便，但结果有一定的残差。积分调节可以很好地减小系统的不平稳而带来的稳态误差，它的缺点就是会减缓系统的控制速率。微分调节则具有超前调节的作用，因此在处理严重滞后的对象时会具有良好的成效。因此，在实际中常把比例、积分、微分调节这3者结合起来使用。尤其是利用二自由度并行控制结构的PID，它可以在实际控制中达到更加良好的调节效果。

2 基于遗传算法的改进二自由度PID控制器

2.1 GA-二自由度PID控制器的基本原理

基于遗传算法的改进二自由度PID控制器的设计由两部分组成：一般的二自由度PID控制器和遗传算法模块组成。被控制对象由二自由度PID进行重复性的控制，而对于遗传算法，它按照对应的算法流程，对二自由度PID的Kc1、Kc2、Td1、Td2、Ti2这5个参数进行一代代的优化下去。同时，不断地同步调整PID的这5个参数值，快速找出最优值，以便于让主汽温控制系统的目标值跟踪特性和抗扰动特性能同步快速到达最佳控制状态。这样，系统就能够快速稳定的输出。遗传算法模块中将二自由度PID的Kc1、Kc2、Td1、Td2、Ti2这5个参数整合在一起作为遗传算法中的每个个体。根据遗传算法流程对个体编码，计算每个个体的适应度，对种群进行选择、交叉及变异操作，这样可以使种群不断繁殖延续，直到寻到全局的最优值为止。GA-二自由度PID结构原理图如图2所示。

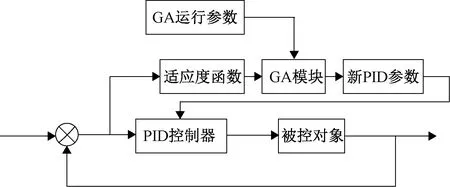
图2 GA-二自由度PID控制器原理图

2.2 遗传算法的实现流程

根据遗传算法的实现过程，对种群进行迭代寻优操作，这个过程将一直持续下去，直到寻到一个最优解为止[11]。遗传算法的操作步骤如下：

Step1 初始化群体生成: 首先利用随机函数产生一个n=100的种群。

Step2 编码方式: 接着利用二进制编码，把Kc1、Kc2、Td1、Td2和Ti25个参数组合在一起，形成一条染色体。

Step3 适应度函数的选取: 适应度函数的选取是至关重要的，选择一个合适、优良的适应度函数对整个寻优过程有着重要意义，它可以直观地表达出个体的好坏。

Step4 选择操作: 对于种群中每个个体的选择，要根据Step3中的适应度函数对每个个体所计算出来的适应度数值来衡量。此外，如果种群中每一代的个体数选择得当，对遗传算法的寻优有着极大的帮助，可以避免种群的快速早熟而带来的寻优过早结束问题。

Step5 交叉操作: 根据实际情况，此次使用单点交叉来进行。

Step6 变异操作: 自然界中，由于各种因素会导致生物基因的突变，进而导致个体变异，表现出新的特征。同样，在遗传算法中，也可以人为地加入一些变异，使群体有更多的表现型，增加种群的多样性。

Step7 解码: 当寻优结束之后，就要对找到的最优值做解码操作，也即把对应的二进制数值变为十进制数值。具体的实现方法如下：若某个参数取值区间是[Umin，Umax]，则该参数可以用长度为m的二进制数值来表示，可表示为x:bmbm-1bm-2…b2b1，上述对应的二进制数值的解码公式为[12]：

(5)

遗传算法的操作流程框图如图3所示。

在遗传算法的寻优操作过程中，终止条件是一个关键部分。因此，对于如何判断系统已经找到最优解，本文以所有种群个体的目标函数值(IAE值)是否一致来作为终止条件。这样可以避免过早收敛、产生早熟现象，可以更准确地寻到最优解。

图3 遗传算法操作流程图

2.3 GA-二自由度PID控制器的参数整定实例

为验证方法的有效性，本文将该方法应用于火电厂火电机组主蒸汽温度控制系统中，通过对该控制系统的辨识，得到被控对象的数学模型为：

(6)

对二自由度的PID控制器的5个参数进行二进制编码，其中Kc1∈(0,10)，Td1∈(0,1)，Kc2∈(0,10)，Ti2∈(0,20)，Td2∈(0,1)每个参数的长度取8位二进制数，5个参数依次串接，形成一个个体，个体长度为L=40，种群大小取n=100。其中，选择算法采用常用的轮盘赌算法。交叉概率一般取0.4～0.9，本文取Pc=0.9，变异概率取0.001～0.1，本文取Pm=0.001 。此外，为了实现超调量、调节时间等时域指标的统一优化，本文的目标函数取绝对误差积分准则：

(7)

对于适应度函数的选择，取当前群体中最大的目标函数值(IAE值)减去当前个体的目标函数值(IAE值)来作为适应度函数。也即:

f=Objmax-Obji

(8)

因此，当某个体目标函数值越大时其适应度函数值越小。而且，在任何一代的种群中，无论目标函数值相差多么接近，适应度函数总会相差很大。且当种群所有个体目标函数值完全一致时，所有个体的适应度函数均为零。故在迭代结束时，种群目标函数已经收敛到一个固定值。例如：假设当前种群有5个个体，目标函数值为[10，10.1，11，11.1，11]，根据公式(8)可得本文选取的适应度函数值为[1.1，1，0.1，0，0.1]。而根据一般情况，适应度函数的选取是由目标函数的倒数所得，其适应度函数值为[0.1，0.099，0.091，0.090，0.091]，可见该方法所获得的适应度函数值相差不大，用轮盘赌方式淘汰个体时，淘汰概率相差不大。而本文所选取的适应度函数所得到的适应度函数值相差较大，有一定的区分度。

3 算例仿真分析

通过遗传算法寻优得到5个参数的最终值与文献[7]采用二自由度得到的5个参数值、文献[8]采用二自由度得到的5个参数值以及文献[13]采用单自由度得到的3个参数值结果，如表1所示。

表1 PID控制器参数值对比

通过进行MATLAB仿真，得到了种群平均IAE值随迭代次数的优化过程。如图4所示。

图4 种群平均IAE值的优化过程

从图中的曲线可以看出：随着迭代次数的增加，不断对种群中IAE值进行寻优选择，最终迭代结束时能够寻得一个最优的IAE值，为 0.591 2。最终寻得的最优IAE值是由目标值跟踪部分的IAE1和抗扰动部分的IAE2，这两部分的最优值之和组成。

通过遗传算法整定后的二自由度PID的阶跃响应曲线和文献[7]中的二自由度PID、文献[8]中的二自由度PID以及文献[13]中的单自由度PID的阶跃响应曲线对比效果展示，如图5所示。

通过以下2个计算IAE和ISE的数学表达式，并运用MATLAB进行计算，可以得到如表2所示的4种情况下的性能指标数值。

图5 GA-二自由度PID与其他3种方法调节效果对比图

(9)

(10)

表2 性能指标值对比结果

通过对图5和表2的仿真结果分析，可以清晰地得到：本文提出的遗传算法改进的GA-二自由度PID无论是目标值跟踪还是外扰动抑制方面，IAE、ISE及ts这3个性能指标的值均优于其他3种方法得到的结果。此外，通过图5还可以清晰地看出本文所提出的方法在超调量和调节时间上也是远远优于其他3种方法。由此可知，本文提出的基于遗传算法改进的二自由度PID在目标值跟踪特性及外扰动抑制特性的控制效果和性能指标上明显要优于其他3种方法。

4 结论

在PID的应用设计中，PID参数的调节是一个重要的环节。本文从二自由度PID和遗传算法的原理出发，将遗传算法应用于二自由度PID参数的调节与优化，并利用MATLAB进行火电机组锅炉主蒸汽温度控制系统的仿真实验。实验结果表明: 对于主汽温系统的控制效果上，基于遗传算法的改进二自由度PID在目标值跟踪特性及外扰动抑制特性等方面的成效均优于文献[7]的二自由度PID、文献[8]的二自由度PID以及文献[13]的单自由度PID。使得输出值最大程度上接近于输入值，减小了系统的误差值，并使得系统具有更小的超调量和调节时间。实验清晰地证明了采用遗传算法对二自由度PID参数调节和优化是有效的，能够获得更好的控制效果，满足了火电厂火电机组主蒸汽温度控制系统的需求。