单脉冲等离子破岩温度场仿真模拟

孙 强 ，刘永红 ，王广旭 ，王晓龙 ，申 泱

（1.中国石油大学（华东）机电工程学院，山东青岛 266580；2.东营市科学技术局，山东东营 257061；3.首都航天机械有限公司，北京 100076；4.清华大学机械工程系，北京100084）

油气资源是关系国计民生、保障国家能源安全的战略性资源。随着油气资源的日益枯竭，能源勘探已经向更深更复杂的地层发展。在勘探开发中，破岩技术尤为关键，破岩效率直接影响钻井速度与钻井成本的高低[1]。在复杂地层中遇到坚硬岩石层时，常规破岩方法能耗高、效率低，无法达到施工要求，尤其是在水平井和小井眼中还易发生钻头磨钝、钻井液漏失等复杂问题[2]。为了解决常规破岩技术在钻进过程中所遇到的问题，各种高效破岩新技术陆续发展：新型钻头[3]（PDC与牙轮复合钻头、新型尖齿PDC钻头）、旋冲钻井[4]、粒子冲击破岩[5]、超临界CO2钻井[6]、高能等离子放电破岩技术[7]等，其中高能等离子放电破岩技术的研究已成为国内外目前研究的热点[8]。

在进行岩石高瞬时能量密度加工时，电源正负极之间高能量会在极短的时间内释放，形成高温等离子体，岩石在高温高压等离子体的作用下，产生熔化、气化以及应力剥落现象[9-10]。由于加工过程复杂、放电时间短且不易观察，热应力难以测量[11]，而数值模拟方法对加工过程中的温度场测量冲破了传统技术的壁垒[12]。本文采用ANSYS有限元分析软件，基于热传导理论，建立了等离子通道破岩过程中的物理模型，对模型进行数值模拟，得到了工具电极与岩石温度场的分布规律；此外，还针对不同工艺参数对模型温度场的影响进行了研究，得到了相应的影响规律。

1 等离子破岩单脉冲放电模型建立

等离子破岩单脉冲放电的物理模型见图1。环状的工具电极紧贴岩石表面，其中内外电极分别接电源的正负极，当电源正负极之间的电压达到一定值，在电解质作用下，正负两极之间形成高温高压的等离子体通道，从而形成脉冲电弧放电，高温的等离子体将超过岩石熔点的区域熔化或气化；同时，由于高温作用在岩石表面形成热应力区域，超过岩石单向应力的区域被剥落与蚀除。

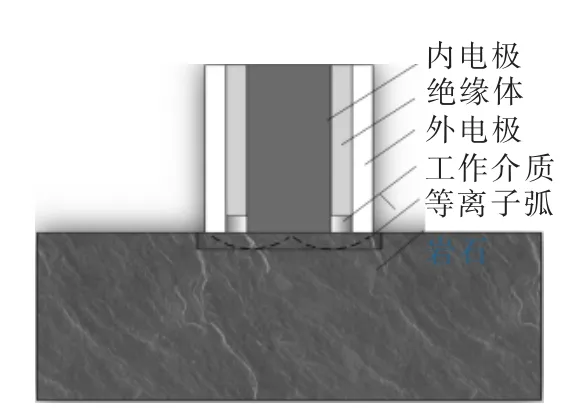
图1 等离子破岩单脉冲放电物理模型

在等离子破岩过程中，瞬间释放大量的能量形成一个瞬时高温热源，能量即以热能的形式分配于工件及电极上。受到放电电流自生磁场的约束作用，根据高斯分布，带电粒子在所形成的等离子通道中分布并不均匀，其密度分布边缘小而轴心大[13]，故热流密度在工件与电极上的分布也符合高斯分布[14-15]，放电通道中的热源分布见图2。

图2 放电通道中的热源分布

高斯热源可表示为：

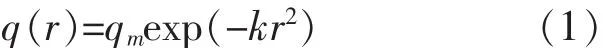
式中：q（r）为半径在 r处的热流密度，J/（cm2·s）；qm为放电通道中心的最大热流密度，J/（cm2·s）；k 为热流量的集中系数，1/cm2；且有k=3/R2，R为放电通道半径。若通道轴心处qm=q0，则随着半径变化的热流密度表达式为：

假设单次脉冲仅在一个位置发生一次脉冲放电，脉冲能量与通道半径直接影响着能量密度值，具体为 q0=3ηUI/（πR2），则上式可描述为：

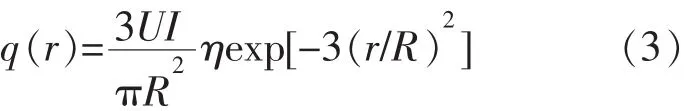
式中：U 为放电电压，V；I为放电电流，A；η为热量分配系数。

2 等离子单脉冲放电温度场模型求解

在等离子放电的物理模型中，环状电极和工件（加工区域假定为圆柱）同轴，等离子破岩的物理模型为完全轴对称模型。因此，本实验热源模型采用高斯分布的线热源模型，将基础二维模型扩展至三维，同时考虑了相变与对流对温度场的影响，并设置定解条件。

2.1 边界条件

常见的导热边界条件有：①已知工件边界上的温度分布；②已知工件表面上的热流密度；③ 已知对流换热系数及其周围介质的温度。热流密度在等离子放电破岩的过程中，其分布特征满足高斯热源特点。此外由于温差的存在，使加工环境、电极和工件之间产生热对流，满足第②、第③类边界条件[18]，用公式表示为：

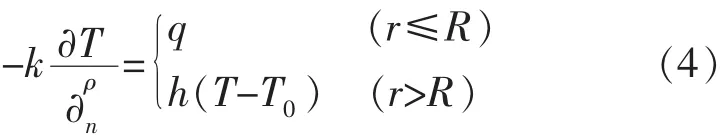
式中：k为热流量的集中系数，1/cm2；q为r方向上的热流密度，J/（cm2·s）；h 为对流换热系数，W/（m2·K）；T为工件表面温度，K；T0为周围环境温度，K。

2.2 初始条件

放电传热开始时，整个模型初始温度即为环境温度，即：

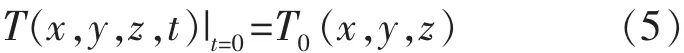
式中：T0（x，y，z）为已知的温度函数，本实验中的初始温度设为20℃。

2.3 等离子单脉冲放电温度场有限元模型建立

图3为模型有限元网格划分。建立等离子单脉冲放电破岩模型时，选用了PLANE55网格单元。实验中网格单元尺寸为2×10-4，平面网格数目为8300，其中岩石网格数目为7500。在放电通道平面上加载已知的空间变化热流密度的温度场模型[19]，求解瞬态热分析。

图3 有限元网格划分

3 计算结果分析

单脉冲放电试验时所用的电解质溶液，其主要成分为水，因此只对水介质中的温度场进行分析。

3.1 模型整体温度场分布

图4是单脉冲等离子放电整体温度分布示意。其中放电电压为1000 V，电流为400 A，脉冲宽度为10 ms，脉冲间隔为10 ms。

图4 单脉冲等离子放电整体温度分布

在正负电极之间施加高压，加之在两极之间绝缘体的隔离作用下形成等离子通道，放电过程中高温区面积较小，最高温度分布在等离子放电通道的中心位置，温度高达19 375℃，这是由于传热不及时，瞬时释放的能量在放电通道中聚集而形成局部高温。根据温度场的分布，云图中温度达到工件与电极熔点以上的材料认为被全部去除。

针对岩石进行分析，在岩石中截取上部径向（x=0～0.03，y=0.01）及中部轴向（x=0.01，y=0～0.01）两部分线段，对节点进行温度分析。图5分别是径向和轴向节点温度分布云图。其中，放电电压为600 V、电流为400 A、脉冲宽度为10 ms、脉冲间隔为10 ms。从径向温度云图可以看出，在热源中心的节点温度是最高的，往两侧逐渐降低且呈现对称趋势，这与高斯热源的热源分布及加载一致；从轴向温度云图中也可以看出，节点温度上部高、下部低，这也证明了热源在模型中得到了正确的加载。

3.2 不同电压条件下工件和电极的温度蚀除情况

图6是保持其他所有参数不变（电流400 A、脉宽10 ms、脉间10 ms），不同电压下岩石径向和轴向节点温度分布曲线。可见，径向节点和轴向节点温度均随着电压的升高而增大，其与横轴所包围的面积亦增加。这表明随着电压的增大，温度所扩展的范围径向更高、横向更深，去除的岩石材料也更多。这可以解释为随着电压的增大，脉冲能量也相应增大，施加在工件和电极上的热量增大，导致工件的温度升高，因而去除的材料增多。

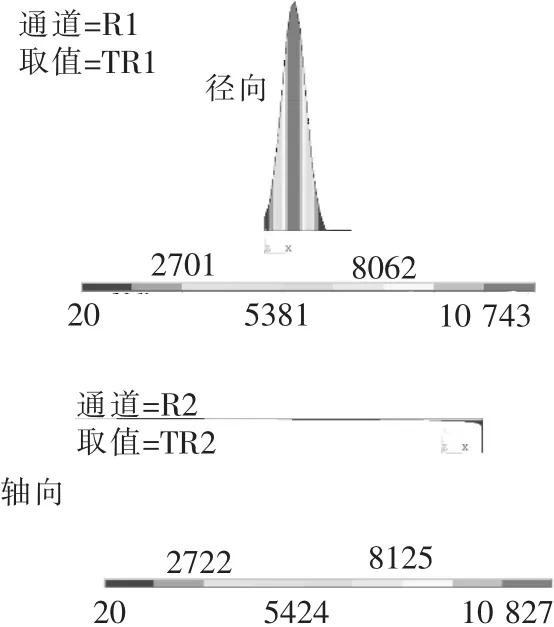
图5 径向节点和轴向节点温度分布云图

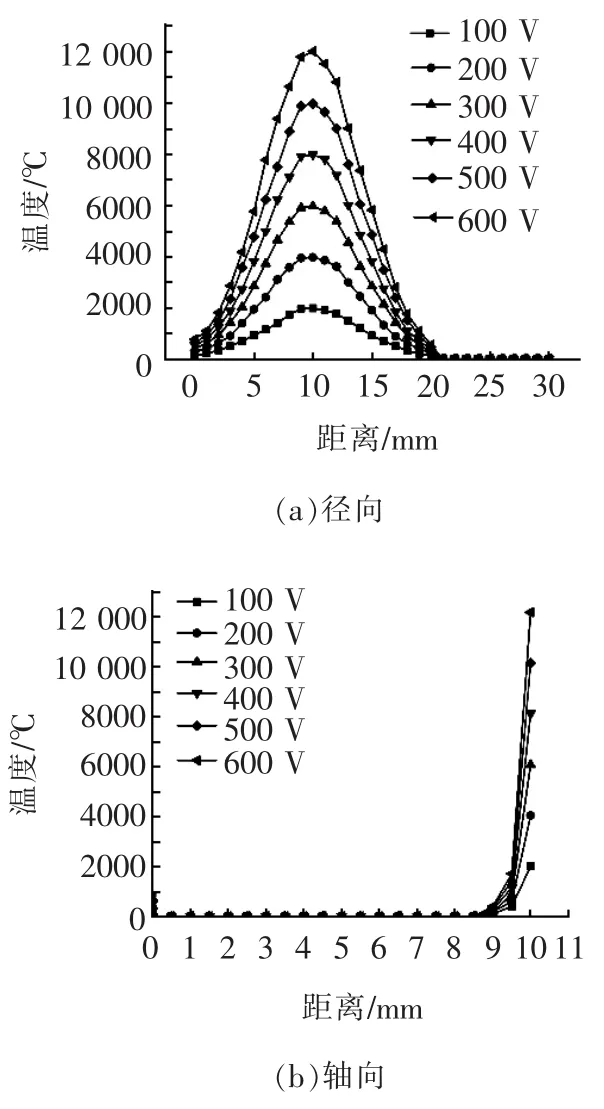
图6 不同电压下岩石径向和轴向节点温度曲线

图7是不同电压下电极的温度分布。由图可知，随着加工电压的增加，电极的最大温度值增加，由3008℃逐渐增加到6005℃再至9022℃，所去除的电极材料的面积也越来越大。

图7 不同电压下电极的温度蚀除

3.3 不同电流下工件和电极的温度场蚀除情况

图8是保持其他所有参数不变（电压200 V、脉宽10 ms、脉间10 ms），不同电流下岩石径向和轴向节点温度分布曲线。可见，径向节点和轴向节点温度均随着电流的升高而增大，其与横轴所包围的面积增加，意味着随着电流的增大，电弧放电的能量提高，作用在工件表面的温度也越高。这表明温度所扩展的范围径向更高、横向更深，去除的岩石材料也更多。这可以解释为随着电流的增大，脉冲能量也相应增大，施加在工件上的热量增大，导致工件的温度升高，因而去除的材料增多。

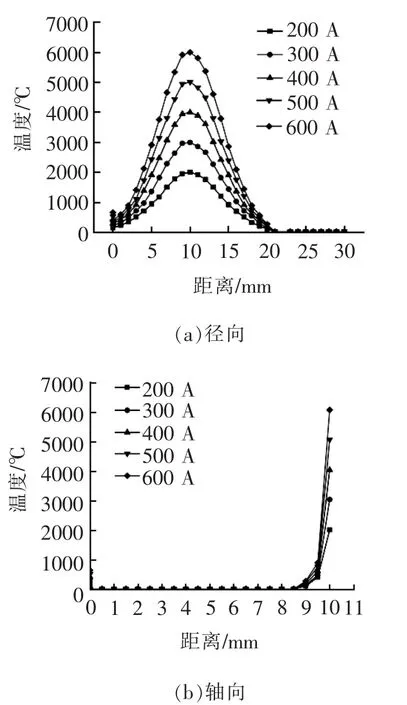
图8 不同电流下岩石径向和轴向节点温度分布曲线

图9是不同电流下电极的温度分布。随着加工电流的增加，电极的最大温度值由3619℃逐渐增加到6005℃再至8425℃，所去除的电极材料的面积也越来越大。

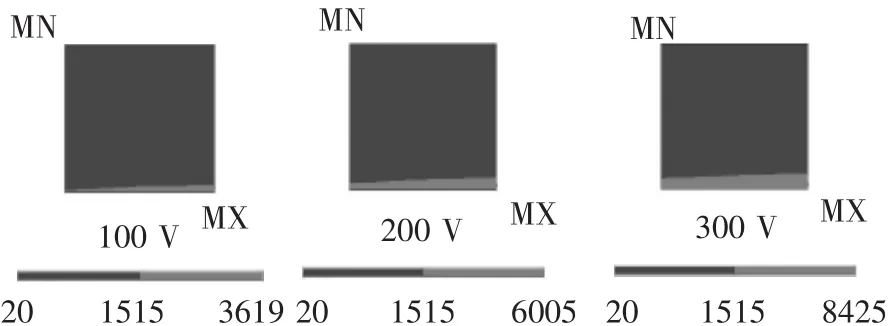
图9 不同电流下电极的温度蚀除

3.4 不同脉宽下的温度场蚀除情况

图10是保持其他所有参数不变 （电压400 V，电流200 A、脉间10 ms)，不同电流下岩石径向和轴向节点温度分布曲线。可见，径向节点和轴向节点温度均随着脉宽的增大而提高，其与横轴所包围的面积增加，意味着随着脉宽的增大，温度所扩展的范围径向更高、横向更深，去除的岩石材料更多。这可以解释为随着脉宽的增大，脉冲能量相应增大，施加在工件上的热量增大，导致工件的温度增大，因而去除的材料增多。

图10 不同脉宽下岩石径向和轴向节点温度曲线

图11是不同脉宽下电极的温度分布。可见，随着脉宽的增加，电极的最大温度值由3821℃逐渐增加到6005℃再至7676℃，所去除的电极材料的面积也越来越大。

图11 不同脉宽下电极的温度蚀除

4 结论

本实验基于热力学理论，通过ANSYS有限元分析软件建立了单脉冲等离子放电破岩加工温度场的有限元分析模型，并对其进行求解，通过仿真模拟得出了模型的温度分布云图与温度曲线，得到不同电压、电流和脉冲宽度对温度场的影响。结果表明，随着电流、电压、脉宽的增大，脉冲能量增大，高温区面积增大，所去除的岩石和电极材料均增多，破岩效率增大。