圆电流和螺线管的磁场分布
2018-11-13董新平
董新平
(许昌学院 电气机电工程学院,河南 许昌 461000)
相对于静电场,稳恒磁场为有旋场,这使得相应的磁感应强度不易直接计算和分析.在经典电磁场理论中,按照毕奥-萨伐尔定律,磁场由电流元产生,通过对载流导线的电流元进行积分可以得到空间中相应的磁感应强度分布.对于具有对称性的载流体如圆电流和载流螺线管,某些特殊位置如其对称轴上的磁感应强度的大小和方向可以利用初等函数的积分以及对称性分析得到.但对于整个空间中的磁场分布不能仅用初等函数进行计算和分析.根据磁矢势与磁感应强度之间的关系B=×A,利用完全椭圆积分函数可以对整个空间中的磁场分布进行计算和分析.基于这种方法,参考文献[1-6] 对圆电流周围的磁场分布进行了详细的分析,参考文献[7-11]对载流螺线管周围不同区域的磁场特性做了对比和数值计算.其研究结果对于理解圆电流和载流螺线管的磁场分布特性起到了重要的作用.但是相应的研究结果对于直观、系统的分析圆电流和载流螺线管的磁场分布还存在一些不足.本文利用椭圆积分函数对相关载流导线的全空间磁场分布进行数值计算和对比分析,便于更全面、直观地掌握圆电流和载流螺线管的磁场性质.
1 圆电流的磁场分布
本节首先利用磁矢势与磁感应强度的关系,给出磁感应强度在柱坐标系中的表达式,然后对圆电流的分布特性进行数值计算和分析.设圆电流的圆心位于原点、半径为a、电流强度为I,此圆电流产生的磁矢势为
(1)
在柱坐标系中作变量代换后矢势A的表示形式为
(2)
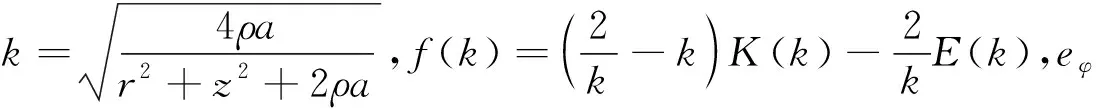
利用磁感应强度与磁矢势的关系B=×A得到柱坐标系中径向和z方向的磁感应强度分别为
(3)
(4)
对于圆电流所在的平面z=0,由方程 (4) 可知径向磁感应强度分量Bρ=0.设Bz0=μ0I/(2πa),纵坐标取值为无标度值BZ/Bz0.Z方向上的磁感应强度分量可由方程(3) 得出,相对应的磁感应强度分布如图1所示.
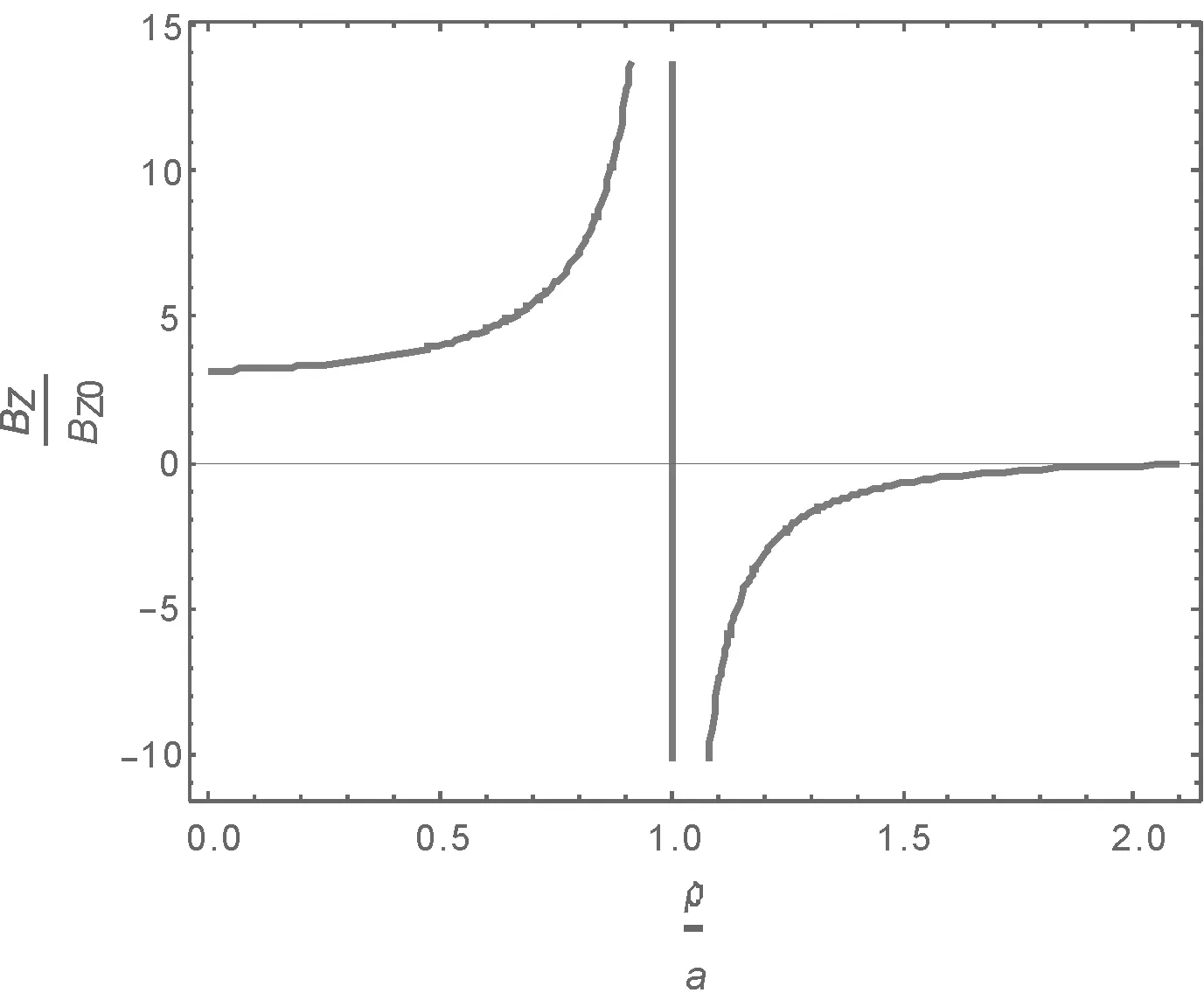
图1 圆电流所在平面上的磁感应强度BZ的分布
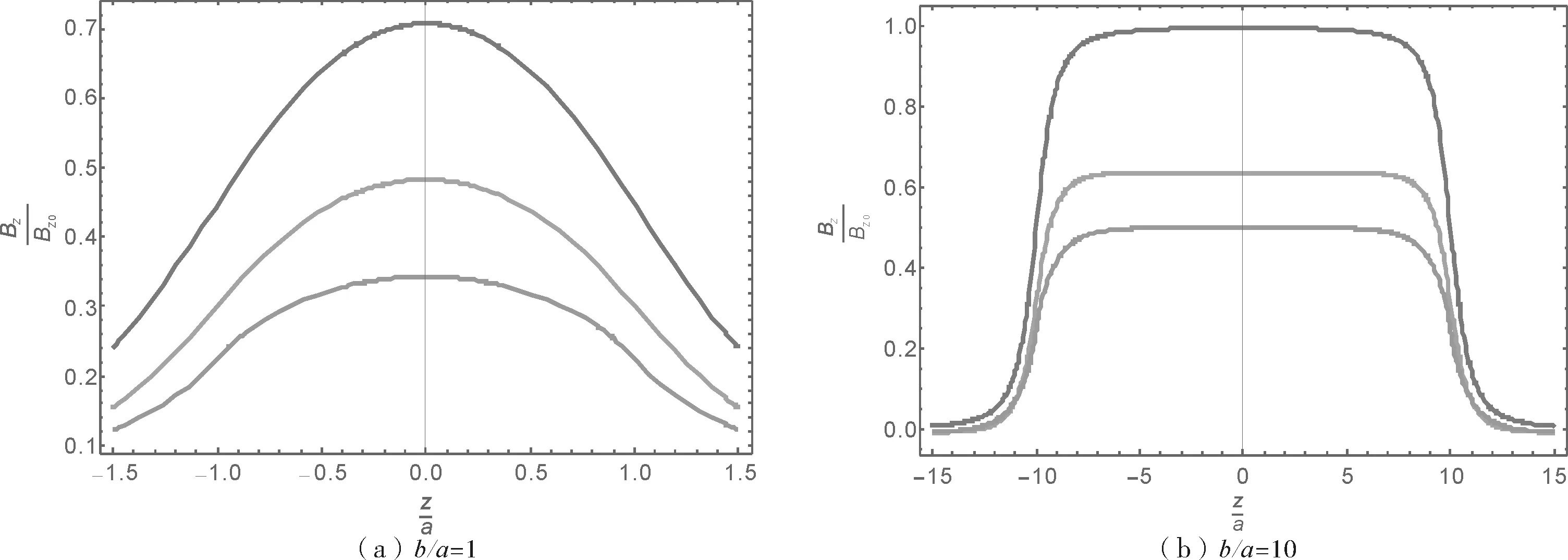
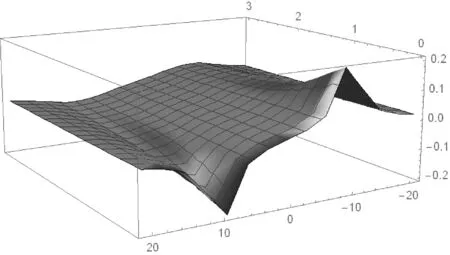
从图1可以看出,圆电流圆心处的磁感应强度Bz=μ0I/2a,与利用初等函数积分得到的结果相同;在圆电流内部0<ρ 设载流螺线管的半径为a、长度为2b,通过的电流为I,单位长度上的线圈匝数为n.在柱坐标下载流螺线管上任取一点Q(a,φ′,z′),该点的面电流密度为 J(Q)=nI(-sinφ′i+cosφ′j) . (5) 点Q(a,φ′,z′)与空间一点P(p,φ,z)之间的矢径为 R(Q,P)=(ρcosφ-αcosφ′)i+(ρsinφ-αsinφ′)j+(z-z′)k. (6) 设载流螺线管上、下两端边缘的轴向坐标分别为z2和z1,由毕奥-萨伐尔定律,载流螺线管在点P处产生的磁感应强度为 (7) 当ρ>0时,利用方程(7)可以得到柱坐标中空间任意一点的磁感应强度的径向和轴向分量[7]. (8) 根据积分区间的对称性,柱坐标下磁感应强度的切向分量Bφ(ρ,φ,z)=0. (9) (10) 根据方程(8)-(10)设定相应的参数,可以对载流螺线管周围空间的磁感应强度进行计算和分析.首先对磁感应强度的纵向分量进行分析.如图2所示,图2中(a)和(b)中自上而下的三条曲线分别对应于ρ=0,ρ=0.5a,ρ=1.1a条件下的纵向磁感应强度分布情况.横坐标为z/a,表示距离螺线管中心点所在平面的高度与螺线管半径的比值,纵坐标表示无标度值Bz/Bz0,其中Bz0=μ0nI.当b/a=1时,螺线管的高度等于其直径,从图2(a)可以看出磁感应强度分量Bz随着距离螺线管中点所在水平面的高度增加而减小;同时在距离对称轴的区域Bz逐渐减小.当b/a=10时,螺线管的高度等于其直径的10倍.从图2(b)可以明显看出,在螺线管内部对称轴处,Bz近似等于μ0nI,接近无限长螺线管产生的磁场,可以近似视为长直螺线管.螺线管内部远离对称轴的区域,Bz虽然也逐渐减小,但是与图2(a)不同的是,与对称轴距离相等的区域磁感应强度Bz近似相等.在螺线管外部,Bz随着与对称轴的径向距离增加而减小. 图2 载流螺线管周围的z方向磁感应强度分布 取b/a=10,ρ/a=0~3,z/a=0~20,得到磁感应强度的径向分量Bρ在空间中分布如图3所示,其中z方向为无标度值Bρ/Bz0,Bz0=μ0nI.从图3可以看出,在z/a=±10,即靠近螺线管端面处Bρ取得最大值,随着高度继续增加,Bρ迅速减小.同时可以看到,在螺线管外部,当b/a>1时,Bρ随着径向距离的增大而迅速减小. 图3 载流螺线管周围的径向磁感应强度分布 根据磁矢势与磁感应强度的关系和毕奥-萨伐尔定律,对圆电流和载流螺线管的磁感应强度分量进行了分析.随后利用椭圆积分函数对相关载流导线的全空间磁场分布进行了数值计算和对比分析,研究结果将为更准确、全面掌握圆电流和载流螺线管的磁场性质提供帮助.2 载流螺线管的磁场分布

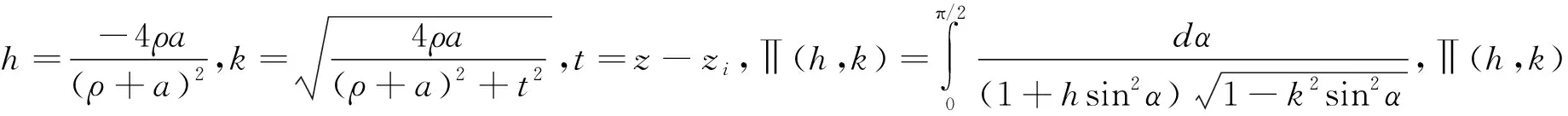
3 结语
