高空作业车风振响应的频域特性分析

，

(江苏师范大学科文学院，江苏徐州221116)

0 引言

作为一种工程机械设备，高空作业车广泛应用在船舶、建筑、市政建设、消防等行业，保证工作平台的稳定和安全是高空作业车研究的关键技术之一。随着高层建筑的不断增加，高空作业车的作业高度越来越高，作业臂长细比越来越大，风荷载效应更为明显。一般认为，结构的风荷载是由静风荷载和随机脉动荷载组成。脉动风分量会引起结构的风激振动，持续的振动除造成结构的疲劳损伤外，由于风载荷作用下可能产生较大的变形和振动[1-3]，严重影响了作业车的安全性和作业人员的舒适性。

高空作业车的常规设计中，常将风荷载等效为静力再考虑一定的风振系数，计算结果不能完全反映风荷载激励下的动力反应。因此有必要对这种高空作业机械进行脉动风荷载下的动力响应分析，以便更好地把握结构的动力性能，提高设计的可靠性。

1 虚拟激励法的基本理论

由振动理论可知，在零初始条件下，线性系统的频率响应函数是输入谐量和输出谐量复振幅之比，即：

(1)

其中：H(ω)为频率响应函数；xω(t)为响应x(t)的傅里叶变换；yω(t)为激励y(t)的傅里叶变换。

系统受到单点平稳随机激励源y(t)作用时，其响应x(t)的自功率谱为：

Sxx(ω)=|H|2Syy(ω)

(2)

式中：Syy(ω)为激励源y(t)的自功率谱密度；H为频率响应函数。其意义是当随机激励被单位激励eiωt代替时，相应的简谐响应为x(t)=Heiωt。

根据虚拟激励法原理，可得到实际响应、实际激励的自功率谱密度和互功率谱密度：

(3)

(4)

(5)

式中：Sxx为实际响应的自功率谱密度；Syx为实际激励与实际响应的互功率谱密度；Sxy为实际响应与实际激励的互功率谱密度。

由此可以获得所需的功率谱矩阵的下列算式：

式中：“*”表示复共轭，“T”表示转置。

2 基于虚拟激励法的风振响应分析

脉动风荷载作用在高空作业车上引起的振动，可看成是多点相干平稳随机激励下的随机振动问题，其动力微分方程为：

(6)

式中：[M]、[C]、[K]为结构的质量、阻尼和刚度矩阵；{Z(t)}分别为节点的位移向量；{F(t)}是作用在结构上的脉动风荷载向量。

根据振型分解法，对(6)式可将位移按振型展开[6-7]：

式中：q为所选取的振型数；uj为第j阶振型的广义位移；φj为第j阶振型向量。

根据规范，一般取Davenport脉动风速度谱作为激励谱，它不随高度变化，自功率谱其表达式为：

(7)

由于脉动风的随机性，考虑各随机激励之间的相关性，引入相关函数coh(ω)，作业臂上相距为r的i、j两点，其水平脉动风速的互谱可表示为[8]：

(8)

式中：

Cx=16，Cy=Cz=10为空间衰减系数。Δx，Δy，Δz是两点间的坐标差。

由式(7)和式(8)式可形成节点荷载功率谱矩阵Spp(ω)。显然，Spp(ω)为非负的Hermite矩阵，可以对其进行LDL*分解。即：

Spp(ω)=L*DLT

式中：L为对角元素均为1 的下三角矩阵，D为实对角矩阵。

取L的第k列向量{Lk}，D的第k号对角元素dk，D可构造n个虚拟激励向量为：

于是求得结构的虚拟响应

式中：H为频率响应函数。

其中，ωj、ζj分别表示第j阶自振频率、阻尼比。

根据(3)式可得响应{z}的功率谱矩阵：

3 高空作业车风振响应分析

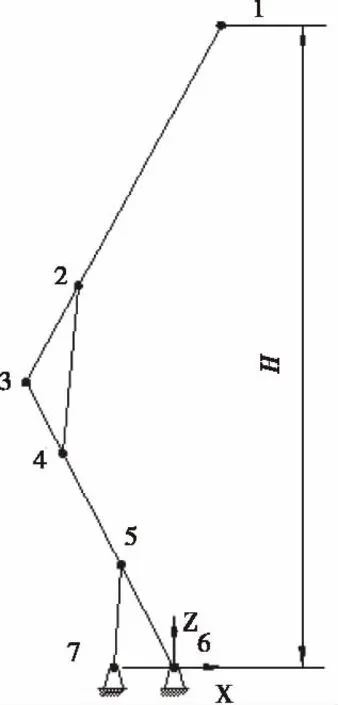
图1 作业臂有限 元模型

本文的研究对象折叠式高空作业臂，由矩形截面的上臂、下臂组成，上臂头部有作业平台，供运送人员和货物，上下臂通过油缸升降。作业臂处在全升高位置时，可将油缸刚化处理，上臂和下臂用Euler-Bernoulli梁单元模拟，油缸用一维杆单元模拟，下臂油缸和下臂端部全约束处理，将作业臂简化为如图1所示的由7个节点、7个单元组成的有限元模型。最大作业高度16 m，l13=7.95 m，l36=7.6 m，l23=0.525 m，l34=1.86 m，l56=1.5 m，l67=0.70 m，E=20700 MPa，上臂截面A1=4.18×10-3m2，I1=4.55×10-5m4，下臂截面A2=4.64×10-3m2，I2=4.87×10-5m4。油缸A=8.12×10-3m2，I=1.58×10-5m4，地貌系数K=0.039，基本风压取0.9 kN/m2，选取Davenport脉动风速谱为标准风速谱，风速作用方向为垂直于作业臂工作平面。在ANSYS中建立作业臂的有限元模型，进行模态分析，取其中有显著影响的前4阶振型，各振型阻尼比均取0.02。前4阶振型频率如表1所示。

表1前4阶振型

在频率范围0.2～30 Hz条件下，编制Matlab仿真程序，得到作业平台(节点1)在10 m/s、15 m/s、20 m/s三种风速下的水平和竖向位移、加速度功率谱如图2-图5。

从图2-图5可以看出，位移响应在4.9 Hz和9.52 Hz两处存在明显的共振反应峰值，对应于第一和第二阶模态振型，其他固有频率处相对较小。而加速度响应则在9.52 Hz和17 Hz处存在共振峰值，对应于第二和第三阶模态振型。随着风速的增加，相应的位移和加速度共振响应明显增大，在风速作用方向的位移和加速度响应大于垂直方向的响应值。

图2 节点1水平位移功率谱 图3 节点1水平加速度功率谱

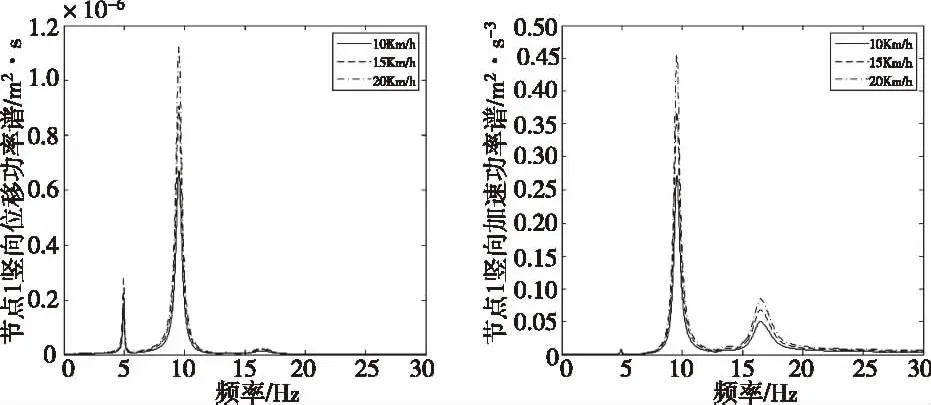
图4 节点1竖向位移功率谱 图5 节点1竖向加速度功率谱

有研究表明[9]，人体在上下振动的敏感频率4 Hz～8 Hz之间，前后振动在1 Hz～2 Hz之间，此时身体部分区域产生共振，随着频率的增加，敏感度下降，而且上下振动对舒适度的影响较大。人体严重的振动响应均在30 Hz以下，而且竖直振动对舒适度的影响为70%，水平方向振动约占12%。为研究振动对作业人员舒适感的影响程度，在用虚拟激励法计算得到响应功率谱的基础上，以该型作业车的最大允许作业风速15 m/s激励时的加速度响应谱，在[1，20]Hz的频率区间，选取一系列离散频点，由(9)式计算1/3倍频程加速度均方根。

(9)

表2和表3分别列出了作业平台处的水平和竖向1/3倍频加速度均方根。根据国际标准ISO 2631全身疲劳/工效降低界限可知，该型高空作业车的加速度均方根都在标准规定的8小时工效降低界限以下，即可以保证工人在8小工作时间内基本不受风振的影响。

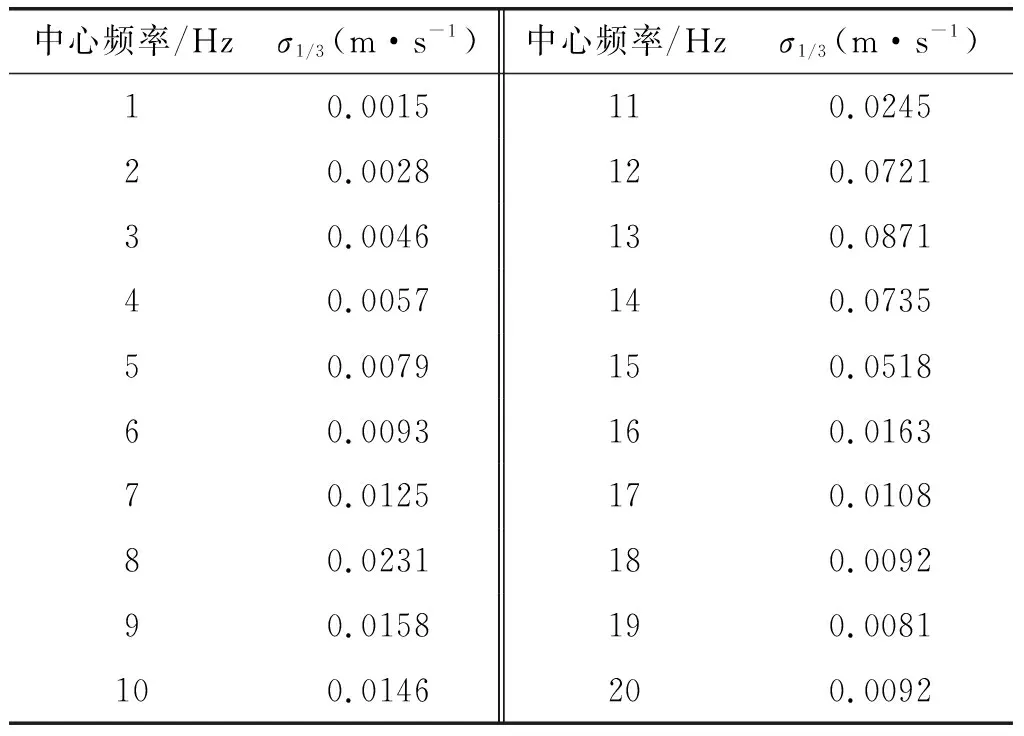
表21/3倍频程加速度均方根(水平方向)

表31/3倍频程加速度均方根(竖直方向)

4 结论

1)基于有限元法和虚拟激励法的高空作业车风振响应分析，可以准确地反映脉动风荷载引起的作业平台振动响应特性，提高了计算效率，为臂架类高空作业机械的风激致振分析提供了可行途径。

2)通过分析作业平台处的水平、竖向位移和加速度功率谱，第1、2阶频率处振动响应明显，风速作用方向的位移和加速度响应大于垂直方向的响应值。

3)作业平台处各频点的1/3倍频程加速度均方根都在国际标准ISO2631全身疲劳/工效降低界限以下，对作业人员的舒适感无明显影响。