基于自主互动、分组合作的初中数学教学探究
2018-11-13汤萍
汤 萍
(江苏省常熟市实验中学,江苏常熟 215500)
引 言
《义务教育数学课程标准》指出:教师教学应该以学生的认知发展水平和已有的经验为基础,面向全体学生,注重启发式和因材施教[1]。学生的学习应该是快乐且积极主动的。想要学生在快乐主动的课堂氛围中提高学习成绩,又能做到“因材施教”,在新课改背景下,创新数学课堂教学策略势在必行,本文将对此做以下探究。
一、延伸课堂,学习任务前置,引导学生自主探索
美国心理学家布鲁姆将认知领域的教育目标分为知道、理解、应用、分析、评价和创造六个层次,前两个层次解决“是什么”的问题,后面四个层次解决“为什么”的问题。传统的课堂教学注重解决“是什么”,而忽视“为什么”。前置学习任务,把“是什么”通过学习任务单的形式提前布置给学生,在课堂上着重引导学生解决“为什么”,通过教师点拨和学生协作讨论,更能让学生获得成就感!
笔者在尝试《二次函数中的相似三角形问题》教学时,提前一天布置了学生学习的任务单。
(1)学习目标:①掌握求二次函数解析式的方法;②运用相似三角形的知识解决问题。
(2)例题:设抛物线y=a+bx-2与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C,且∠ACB=90o(如图1)。
①求m的值和抛物线的解析式;
②已知点D(1,n)在抛物线上,过点A的直线y=x+1交抛物线于另一点E,求点D和点E的坐标;
③在②的条件下,若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标;
④学有余力的学生选做:在②和③的条件下,△BDP的外接圆半径等于___。
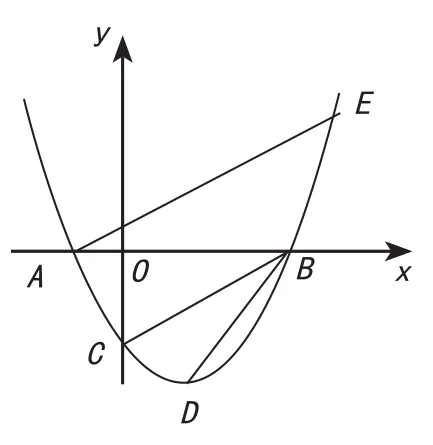
图1
笔者事先制作好微课视频,长度不超5分钟,通过班级QQ群或微信群发布,学习的过程因人而异。学生可快进或不看,也可以重复看,体现了因材施教的个性化教学。师生还可线上互动交流,不仅提高了学习效率,还增强了学生的学习积极性和主动性。
二、回归课堂,分组合作学习,引领学生知识内化
在学生初步理解知识点的基础上,教师就能腾出时间在课堂上知识内化。根据班级学生特点,笔者进行了异质分组,小组成员协同完成学习任务,在学生完成练习时,教师适时对有困惑的学生进行小范围讲解,及时有效地给予有针对性的指导,真正做到引领学生学习。
《二次函数中的相似三角形问题》中学习任务已经前置,回到课堂首先检查学生掌握情况,选择小组代表来讲解;根据讲解情况评出优秀小组,以激发学生自主学习的积极性。检查发现求二次函数解析式完全没有问题,但相似三角形的确定普遍有困难,于是就引导学生要确定相似三角形就要找对应关系,那就必须分类讨论。
有学生指出:“△AEB是钝角三角形,那么△PBD也是钝角三角形!”
“△PBD中哪个角能为钝角?”进一步点拨,“点P在x轴上,首先考虑点P在B的哪一侧?”
学生抢答:“不可能在点B右边!因为如果在点B右边的话∠PBD大于∠ABE,两个钝角不相等了,不可能相似!”
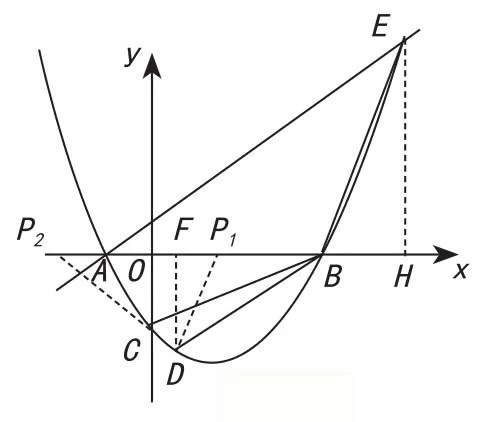
图2
笔者立即予以肯定,此时小组开始积极讨论,问题终于明朗了:∠EAH=∠DBF=45°,所以∠DBH=135°,90°<∠EBA<135°,点P只能在B的左侧!由此还知道隐含在题目中有一对角相等,即∠EAB=∠DBP=45°,那么只需分两类情况进行讨论,即①△DBP1∽△EAB;②△DBP2∽△BAE。解答如下:
(1)若△DBP1∽△EAB,则
(2)若△DBP2∽△BAE,则
巩固练习:已知抛物线y=a(x+3)(x-1)(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=﹣ 3x+b与抛物线的另一个交点为D.
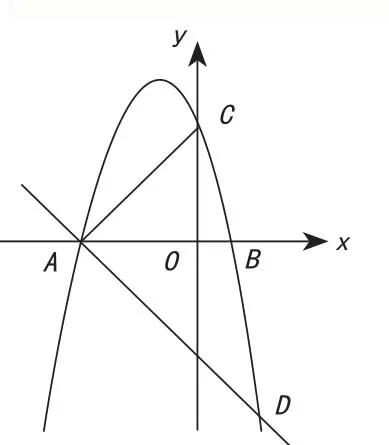
图3
(1)若点D的横坐标为2,求抛物线的函数解析式;
(2)若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标。
最后总结:相似三角形首先要找对应关系,在上面的两个问题中不难发现,都能找到一对对应角相等,故而可以缩小分类讨论的范围。在课堂上探讨解决“为什么”,使学生获得充分的成就感。
三、巩固课堂,反思教学策略,引发学生能力提升
(一)前置学习应“提层次”和“降门槛”
任务单内容面向全体学生,一般教师考虑的是中间层学生,所谓“提层次”是针对“尖子生”来说的[2]。例如,在《二次函数中的相似三角形问题》一课中,任务单例题中最后一个问题就是“提层次”,满足了“尖子生”喜欢难题的心理,利用他们相对空余的时间让他们“吃饱”一点。那么“降门槛”就是针对“学困生”的,布置的任务单要以增强他们的学习信心为宗旨;可以事先单独交流沟通,降低一定要求,定好应该完成的任务,在课堂上多关注,让他们也能参与讨论发言,给他们信心。
(二)课堂教学应“抽跳板”和“搭台阶”
小组合作学习中每组都由数学相对较强的学生任组长,容易滋生“养尊处优”的心理,所以笔者在课堂中适时运用“抽跳板”的办法,增加困难,为了能让他跳得更远。例如,笔者在巩固练习中增加了第(3)问:在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
在其他学生完成基本题时,这些数学“骨干分子”就做这个难题,教师给予引导,画出辅助线;但在关键点上突然停住,让他们自主探索,吊足“胃口”时抽掉“跳板”,让他们自己迎难而上。
解答:作DM∥x轴交抛物线于M,作DN⊥x轴于N,作EF⊥DM于F,
∴ 当BE和EF共线时,最小,则BE⊥DM,∴E(1,)。
当然,更多的是当学生遇到困难时,教师及时伸出援助之手,为他们搭台阶。可能只是一小步,但就是这一步台阶,能让他们登上自己的又一个新高度。
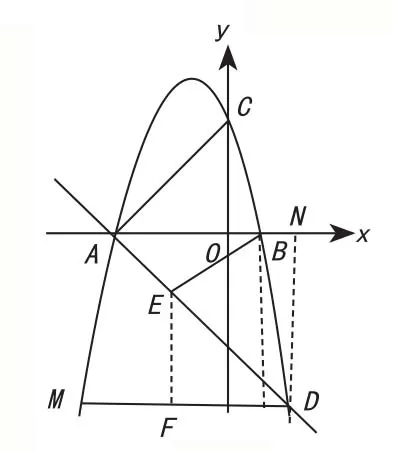
图4
结 语
反思自己的教学实践,笔者认为采集学生在前置学习和课堂学习中的典型错误案例很有必要,因为这些是来自于学生的真正的问题。师生互动当堂解决这些问题,可以达到课堂共鸣的效果。同时,分小组合作学习,激发团队精神,形成积极向上的学习氛围,在潜移默化中助力学生能力提升。自主互动学习有机结合、分组合作学习内部驱动,笔者想这样的课堂教学过程才是学生的一次主动、愉快的探究之旅!
