基于近邻响应的SEIR网络舆情信息扩散模型研究

张 伟

(华东政法大学社会发展学院，上海，201620)

1 引言

信息是网络舆情的载体，网络舆情的扩散过程也就是网络舆情信息在互联网空间中借助在线社会网络实现的信息迁移过程。因此，研究网络舆情信息扩散对我们理解网络舆情的发展变化规律，制定适宜的应对措施具有重要意义。

罗杰斯提出，扩散是“信息在社会系统成员中，经由一定时间，借助特定渠道的传播过程”，它本质上是“为了使信息为社会成员所共享的信息交换过程”[1]。就信息扩散的渠道而言，“大众传播媒介在使受众获得关于某种信息的初步认识上更为快速便捷，……而人际传播渠道——尤其是参与信息扩散的个体在某些重要社会性征上较为相似时——能够更为有效的说服民众接受信息，从而加强信息扩散的效用”[1]。当前流行的在线社交网络中的信息扩散过程更是突显出基于社会网络的人际传播效应，有研究者指出，微博等在线社交网络平台之所以具有深刻的社会影响力，最主要的原因就是其中的信息传播过程是“点对面”的即时传播，且建立在叠套的社会关系网络之上，并以用户间的信任关系为背书[2]。就网络舆情信息扩散而言，在初始状态下，网络中存在一些活跃节点，它们最早接受舆情信息，甚或本身是相关信息的发布者，其他节点因受到活跃节点的影响而从非活跃状态转变为活跃状态，通过该过程的不断反复，最终实现网络舆情信息在网络空间中的大范围扩散[3]。

基于扩散机理上的相似性，很多研究者借鉴SIR、SEIR等传染病动力学模型来探究网络舆情信息的扩散和演化规律。以传统的SEIR模型为例，特定区域内的人群被划分在易感者(Susceptible)、潜伏者(Exposed)、传染者(Infective)和移出者(Removed)四个仓室之中，处于不同仓室的个体受到接触带来的影响，可能发生状态上的转移，其整体呈现为图1所示的线性概率过程，其中λ、ω和γ为相邻仓室个体的转移概率。

图1 传统的SEIR模型

由此可见，传染病在人群中的扩散主要是通过微观层面的个体接触而实现的，SEIR等传统的传染病扩散模型通常建立在均匀混合假设(HomogeneousMixingHypothesis)之上，也就是说，这些模型一般假定个体之间具有完全相同的接触率和传染性，没有考虑由接触个体构成的复杂社会网络的拓扑结构以及个体异质性等因素对传播过程的影响。随着小世界网络[4]和无标度网络[5]在真实系统的发现和建立，研究复杂网络上的传染病动力学引起了研究者的广泛关注[6]。事实上，引入接触网络的概念，将接触过程限定在近邻个体之间能够更为真实地描述现实世界中的疾病或信息的扩散过程。从网络的意义上来说，传统的基于常微分方程而建立的传染病扩散模型可以看作是发生在全局耦合网络上的扩散行为，相对来说，真实社会系统中的社会网络不仅更为稀疏，而且呈现出聚集性、小世界性等特征，这就需要在传统的传染病扩散模型的基础上考虑接触网络拓扑特性的影响[7]。就此而言，Goldenberg提出的级联模型[8]以及Schelling、Granovetter等人提出的门槛模型[9-10]能够帮助我们更好地理解这一过程。在级联模型中，网络中的每个节点在自身转变为活跃状态后，都会以一定的概率去激活它的邻域节点，如果激活成功，那么其邻域节点也会变为活跃状态；门槛模型则指出，每个节点都有自己的信息接受门槛，并受到活跃邻居节点的影响，节点只有在其邻居节点的影响值大于自身的信息接受门槛时，才会向活跃状态转变[7]。

虽然网络舆情信息扩散过程复杂多变，同时还有很多不确定的影响因素，但是，网络舆情信息扩散过程也有其内在的机理和规律可循。根据前文的分析，网络舆情信息传播除了受到信息特性的影响之外，最主要的影响因素就是发生网络的结构特性[11]。为此，本文从网络舆情信息扩散中微观层面的个体互动过程所具有的特征着手，构造了一种基于近邻响应的SEIR网络舆情信息扩散模型，并利用仿真实验分析了网络结构及信息源对网络舆情信息扩散效果的影响。

2 网络舆情信息扩散中的微观交互模式

2.1 网络舆情信息扩散中的个体接触过程

在网络舆情信息扩散的过程中，传统社会中的大众传媒和人际传播这样两种信息传递通道呈现出相互交融的趋势，多样化个体之间的交互传播成为网络舆情信息扩散的主要途径。由PEW网络研究中心实施的一项关于Facebook的调查研究表明，Facebook以及类似的在线社交网络已经成为突发性新闻最好的发布渠道[12]，而Facebook等在线社交网络不仅包含一般网络个体，同时也包含“大众传媒”之类的特殊个体。因此，宏观层面的网络舆情信息扩散过程事实上是通过微观层面多样化个体的接触过程而实现的[7]。具体而言，在以社交网络、微博为代表的新兴社会化媒体中，突发性网络舆情信息总是由网络中的少量个体率先发布，然后通过个体社会关系网络中其他个体的转发或分享等在线行为传播给一个个与其具有连接关系的信息接收群体，经由虚拟的社会关系网络，使网络舆情信息的“感染群体”规模不断扩大，进而形成不容忽视的社会力量[13]。

图2给出了网络舆情信息扩散中的个体接触过程示意图。从中可以看出，网络舆情信息从知情者(图中的实心圆)向非知情者(图中的空心圆)的传播以个体间的连接关系为纽带，最终蔓延至整个线上人际关系网络。网络舆情信息扩散的这种微观个体接触过程及其内在机理与传染病的接触型传播相似，它们都是依靠接触关系而实现传染或影响范围的不断扩大。相比于传染病的扩散，网络舆情信息扩散过程中由个体接触带来的个体状态转移虽然同样受到信息发布源或转发源的影响，但是，这一过程还渗透了个体的主观意愿，也就是说，只有个体愿意在接触过程中转发或分享来自其他个体散布的信息，他才会成为该信息的新传染源，否则只会处于知情的状态，从而造成整体扩散网络中某一条传播链的暂时或永久断裂[7]。

2.2 网络结构对个体接触过程的影响

扩散发生在社会系统之中[1]，因此，研究网络舆情信息扩散需要持有系统观，将网络舆情信息扩散视为互联网空间中相互连接的个体之间交互作用的一种动态过程。网络空间中的个体交互作用事实上是通过虚拟的个体接触行为实现的，这里所说的虚拟性具有两层含义：其表层是空间的虚拟性，亦即发生接触行为的不同个体的身体是不在场的，他们凭借网络空间中的虚拟社会关系而彼此影响；其底层是过程的虚拟性，网络空间中的个体接触归根结底是信息的流动，信息在不同个体之间经由虚拟关系网络而实现的传递和迁移是个体接触过程的主要表现。在网络舆情信息扩散过程中，个体对舆情信息的感知依赖于所处的社会网络结构以及个体在网络中所处的位置。就此而言，个体之间的关系网络对于网络空间中的个体接触过程既有限制也有强化，其限制作用体现在接触过程必须经由连接而实现，没有路径相连的个体之间是不可能发生接触行为的；其强化作用在于受到个体关系网络某些结构特性的影响，表面上相距甚远的两个个体只需通过非常有限的转接就能实现相互影响[7]。“结构洞”理论的提出者Burt研究了网络聚合性(Cohesion)和结构等价性(StructuralEquivalence)对个体接触过程的影响[14]，其中，聚合性关注个体与他人之间的社会化过程，个体间的接触行为发生得越频繁，那么他人对某一信息的接纳行为就越有可能引发个体自身对该信息的接纳；结构等价性所要说明的是社会关系网络中具有相似结构的个体，其行为也具有较强的相似性。

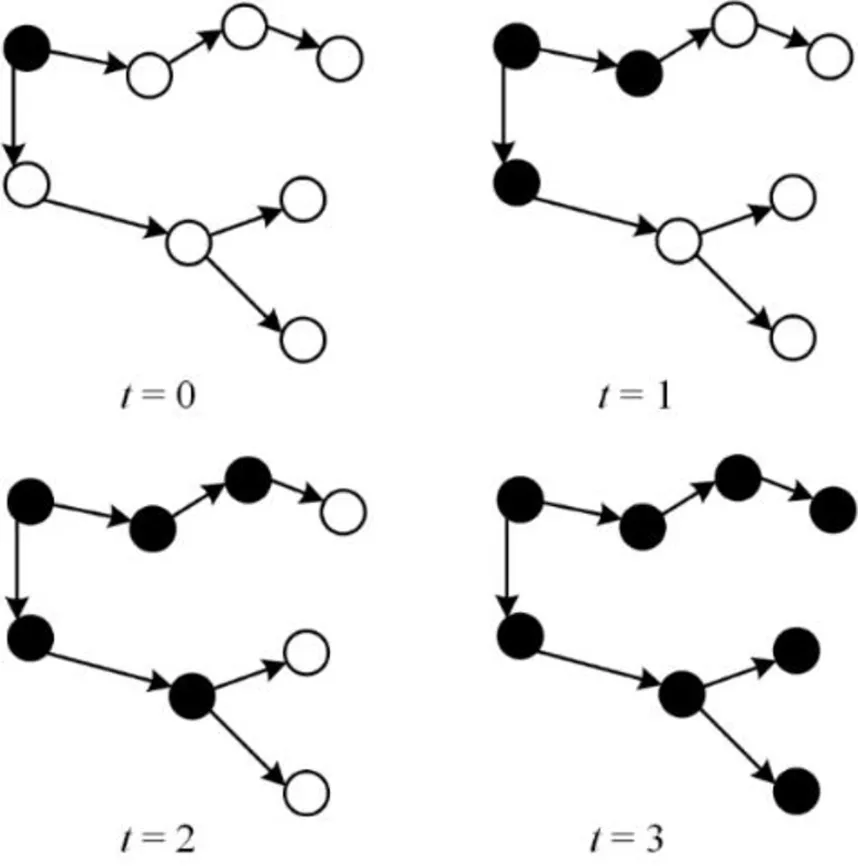
图2 网络舆情信息扩散中的个体接触过程

总而言之，个体所处网络结构的不同以及在同一网络中所处位置的不同都会对个体接触过程产生影响。在研究网络舆情信息扩散的过程中，网络结构差异带来的影响可以通过对不同类型复杂社会网络的比较研究中获得；而由所处网络位置的差异性造成的个体接触过程和最终信息扩散效果的差异，则可以通过分析网络的静态属性特征来揭示，比如存在于非均匀网络中的富节点容易形成“富人俱乐部效应”[15]，一般节点与之相比在接触过程和作用模式上都会呈现出显著的不同。

3 网络舆情信息扩散模型的构建策略

3.1 网络舆情信息扩散中的个体状态转移

信息在网络中沿着连接各节点之间的边而流动，其中伴随着各节点的决策以及由此导致的状态而变更。一般来说，信息流动引发的网络个体行为取决于如下几个因素：各节点如何决策以及如何变更状态；被分享信息的性质；网络中的节点如何连接[16]。围绕这样几个因素，在分析网络舆情信息扩散中的个体状态转移时，需要关注如下三方面的内容：一是网络舆情信息扩散网络的结构特性；二是网络中各节点的状态；三是网络中各节点的决策过程[7]。

在互联网空间中传播和扩散的网络舆情信息并不是孤立存在的，它是某一事件或话题及其衍生出来的其他事件或话题的综合体。由于互联网空间的开放性以及个体在信息流动过程中扮演角色的多样化，个体不再像传统大众传播媒介体系中那样被动地接受信息，他们可以主动参与到信息流动的整个过程。借用传染病模型对个体状态的划分方法，在网络舆情信息扩散的过程中，个体通常可以被划分为四种状态：第一是非知情状态(S)，他们暂时没有受到网络舆情信息的影响，对网络舆情缺乏认知，但是，受到个体关系网中其他邻接个体的影响而具有状态转移的可能性；第二是知情状态(E)，处于该状态的个体对网络舆情信息有一定的了解，但是受到个体兴趣或其他因素的影响，他们暂时(也可能永久)不会将其继续传播；第三是传播状态(I)，这些个体是网络舆情信息扩散的主要推动者，受其影响，处于非知情状态的个体才有可能摆脱非知情状态而进入知情状态或传播状态；第四是移出状态(R)，该状态的个体失去了对网络舆情信息的传播兴趣而处于对信息免疫状态[7]。不同于传统SEIR模型所呈现的线性概率过程，网络舆情信息扩散中的个体状态转移过程表现出一种非线性结构，具体如图3所示。

网络舆情信息在互联网空间中生成后会沿个体中心网延伸到整个网络，由图3可见，处于非知情状态的个体受到传播状态个体的影响，会以一定的概率转移到传播或者知情状态；处于知情状态的个体受到传播个体的持续影响，可能以一定的概率向传播状态转移，同时也可能失去对该网络舆情信息的兴趣而以一定的概率直接转移到移出状态；此外，处于传播状态的个体则会以一定的概率向移出状态转移。在个体状态转移的过程中，本文设定网络舆情信息扩散过程需要满足三个假设条件：第一，网络舆情信息扩散网络是静态的，个体及其之间连接所构成网络的统计特性和拓扑结构在网络舆情信息扩散的整个过程中都保持不变；第二，个体发布或转发网络舆情信息之后，他的邻域个体都会受到相同的影响，也就是说，不存在由于缺场等原因造成无法接收信息的情况；第三，直接的接触过程只能发生在有边相连的个体之间，无边相连的个体只有可能通过他们之间的路径发生间接接触[7]。

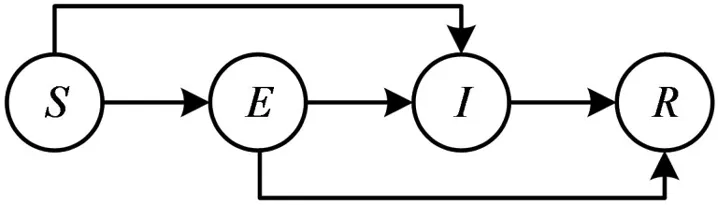
图3 网络舆情信息扩散中的个体状态转移过程

3.2 网络舆情信息扩散模型的建立

根据图3所呈现的网络舆情信息扩散中的个体状态转移路径及其条件限制，可以用微分方程组的方式建立网络舆情信息扩散模型。首先设群体规模为N，{1,2,3,…,n}为其中的所有元素，并组成一个复杂关系网络G(N，E)，E表示网络中边的数量。由于信息的扩散具有方向性，因此，G是一个有向网络，其中的个体只能受其点入个体的影响，并将这种影响扩散至点出个体。令P(k)表示点入度(所有点入个体的数量)为k的个体在网络中出现的概率，则网络的平均点入度可以表示为〈k〉=∑kP(k)。设时刻t网络中非知情状态、知情状态、传播状态和移出状态的个体数量分别为S(t),E(t),I(t)和R(t)，它们在群体中所占的比例分别为s(t),e(t),i(t)和r(t)，则有s(t)+e(t)+i(t)+r(t)=1，根据Burt提出的结构等价性理论，可以认为，度相同的个体具有相似的行为表现，由此可利用平均场的方法建立如下微分方程组：

(1)传播比：在系统运行的时刻t，处于信息传播状态的个体占全部个体的比率，它的值为i(t)。

(2)知情比：舆情信息在时刻t的覆盖范围，记为z(t)=e(t)+i(t)+r(t)=1-s(t)。

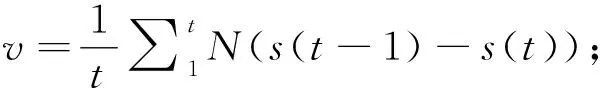
4 模型仿真结果

本文使用Matlab2014a对建立的网络舆情信息扩散模型进行仿真实验。考虑到现实中在线社交网络在度分布、聚集系数、路径长度等方面具有的拓扑特性[19]，仿真过程中主要用到的个体关系网络是在BA无标度网络[5]的构造逻辑下利用Pajek5.01生成，该网络的主要特征如表1所示。

表1 仿真实验中的网络特征

4.1 复杂网络中的网络舆情信息扩散过程

从宏观上来看，网络舆情信息扩散过程表现为网络舆情信息覆盖面的逐渐扩大；而从微观上来看，这一过程则表现为个体状态的不断转移。由于初始时刻网络中的舆情信息传播者在人群中占有很低的比例，因此，可以假定t=0时，网络空间中非知情状态、知情状态、传播状态和移出状态的个体比率s(t),e(t),i(t)和r(t)分别为0.98、0.00、0.02和0.00。另外，模型中使用的参数为λ=0.2，γ=0.2，M=3，t=200。仿真结果如图4(a)所示。从中可以看出，网络舆情信息扩散过程最终以四种状态的个体比重保持稳定而结束。在整个扩散过程中，网络中的非知情个体数量不断下降，最终在群体中所占的比例只有2.2%；移出状态个体的数量不断增长，最终达到个体总数的88.2%；处于知情状态和传播状态的个体数量都经历了先增长后衰落的过程，这两种个体所占的比重最终分别为9.6%和0.0%，其高峰分别出现在t=35和t=45，高峰时刻的比重分别为30.4%和15.0%[7]。由此可见，舆情信息可以在较短的时长内实现大范围的扩散。

图4(b)给出了传统SEIR模型的信息扩散过程，通过比较可以看出：虽然网络中节点之间的连接比传统SEIR模型小得多(在传统的SEIR模型中，群体中的个体是同质混合的，任意两个个体之间都有可能发生接触行为，因此，其扩散网络为全局耦合网络，该网络中的连接数量E=N(N-1)/2，但是信息扩散的效果并没有表现出显著性差异；在本文构建的基于近邻响应的网络舆情信息扩散模型中，系统趋于稳定时群体中仍有一定数量的知情状态个体，而在传统SEIR模型中，这部分个体则随着系统的运行而最终完全消失，就此而言，本文构建的模型更能描述舆情信息的扩散过程。事实上，在某一舆情事件的演化过程中，知情状态个体的数量在多数情况下要多于传播状态的个体，而且他们不会随着舆情事件的结束而完全消散，这些人可能在未来某一时刻推动相似舆情事件的生成与发展[7]。

图4 模型仿真结果

因此，在传统SEIR的基础上，将网络舆情信息扩散的路径限制在具有一定结构特性的社会关系网络中，同时考虑个体交互及状态转移的特殊性，构建基于近邻响应的SEIR模型能够更好地拟合网络舆情信息的扩散过程。

4.2 网络结构对网络舆情信息扩散效果的影响分析

网络类型的差异最能体现网络结构特性上的不同，为此，本文模拟了五种最典型的网络舆情信息扩散网络，即全局耦合网络(GL)、ER随机网络(ER)、最近邻耦合网络(NN)、小世界网络(SW)和BA无标度网络(BA)，其中的后四种网络均具有相同数量的节点和边。设模型参数的取值为λ=0.2，γ=0.15，M=3，初始传播节点由系统随机选定，其数量为5。针对每一种网络类型，分别进行50次循环实验并取其均值，可以得到图5所示的结果。

图5 网络类型对网络舆情信息扩散的影响

由于网络性质的差异，网络舆情信息在不同网络中的传播效果也表现出较大的差异性。从图5可以看出，仿真使用的五种网络在传播比的变化上具有显著差异，其中，最近邻耦合网络的传播比变化曲线最为平缓，同一时刻参与舆情信息传播的个体最多，占2.12%，其他四种网络中的传播比变化呈现出明显的单峰形，全局耦合网络最为陡峭，其次为BA无标度网络，小世界网络和ER随机网络紧随其后，但这二者的差距不大。就网络舆情信息的扩散程度而言，五种网络的最终知情比分别为0.9990、0.8357、0.2120、0.9796以及0.9810，可见，网络舆情信息在最近邻耦合网络中的扩散程度最低，但是，在全局耦合网络、BA无标度网络和小世界网络中则不存在明显差别，这三种网络虽然统计特性不同，但都具有较好的连通性。因此，连通性对于网络舆情信息扩散具有重要影响，它是舆情信息能否在大范围扩散的关键因素。从网络舆情信息扩散的速度来看，在个体数量固定的情况下，五种网络中瞬时速度的变化也基本遵循全局耦合网络峰值最高，BA无标度网络其次，小世界网络和ER随机网络紧随其后，最近邻耦合网络最低的情形。

网络类型可以从整体上反映网络结构特性的差异，但从具体上来说，网络结构差异则体现在一系列网络统计特征上，如网络规模、网络平均度、富人俱乐部系数等[7]。由于BA无标度网络同时体现了在线社会关系网络的小世界性、无标度性、层级性和富人俱乐部效应，这与网络舆情信息扩散的发生网络具有同构性，因而使用BA无标度网络对网络舆情演化网络进行拟合可以达成最佳效果[20]。为此，选取不同的BA无标度网络来分析网络舆情信息扩散过程，可以探知网络规模、网络平均度、富人俱乐部系数等网络特征对网络舆情信息扩散效果的影响。

图6给出了不同规模BA网络中的舆情信息扩散效果。从中可以看出，按照相同的构造算法，当网络规模N分别等于100、200、500及1000时，所有个体的传播比和知情比不具有显著差异，也就是说，网络规模对网络舆情信息扩散程度影响较小。就网络舆情信息扩散的瞬时速度而言，在系统趋于稳定前，网络规模越大，瞬时速度也相对越快，同一时步新增的舆情信息知情者越多；同时，网络规模越大，系统达成稳定所耗时间越长，舆情信息平均扩散速度也越快[7]。这一实验结果与真实世界中的网络舆情信息扩散情况相吻合，虽然真实的在线社会关系网络规模庞大，但是，舆情信息同样能以较快的速度获得较高的知情比。

图6 网络规模对网络舆情信息扩散的影响

由于BA无标度网络的构造遵循增长和优先连接的特性，因此，通过调节每一时步新增节点与既有节点连边的数量可以得到具有不同平均度的网络。设初始节点数量为20，这20个节点构成一个边等于111的ER随机网络，每一时步新增节点与既有节点连边数κ分别为1、5、10、15和20可以得到五个平均度分别为〈k〉=2×(222+480×κ)/500的BA无标度网络。图7给出了网络舆情信息在这五个网络中的扩散结果，从中可以看出，当κ>5时，网络舆情信息的传播比不具有显著差异；随着κ值的增加，网络的连通性也越加紧密，网络舆情信息扩散的瞬时速度在有限时间内也相对越高，同时，除κ=1所生成的网络之外，另外四个网络在系统达成稳定所耗费的时间以及平均扩散速度上的差异并不明显。因此，网络舆情信息扩散效果在一定范围内对网络平均度具有敏感性，不过其阈值相对较低[7]。

图7 网络平均度对网络舆情信息扩散的影响

与其他几种网络统计特性相比，具有富人俱乐部效应的网络相对较少；而在现实生活中，特别是网络空间中的社会网络很少是均匀的，其中存在少数具有大量连接的“富节点”，这些富节点倾向于彼此相连形成富人俱乐部。为了探究网络舆情信息扩散效果对网络富人俱乐部系数的敏感性，本文首先按照BA无标度网络的构造算法，以节点数为5且边随机生成的初始网络为基础生成κ=3且规模为500的网络A，该网络中度超过30的节点有7个，其连接状况如图8(a)所示，这7个节点的连通性，亦即Θ(r=7)=0.4286；删除其中的若干个连边，同时随机向其他节点添加相同数量的连边，可以得到相似的另一个网络B，该网络度排行前7的节点连接图如图8(b)所示，其富人俱乐部系数Θ(r=7)=0.1429。

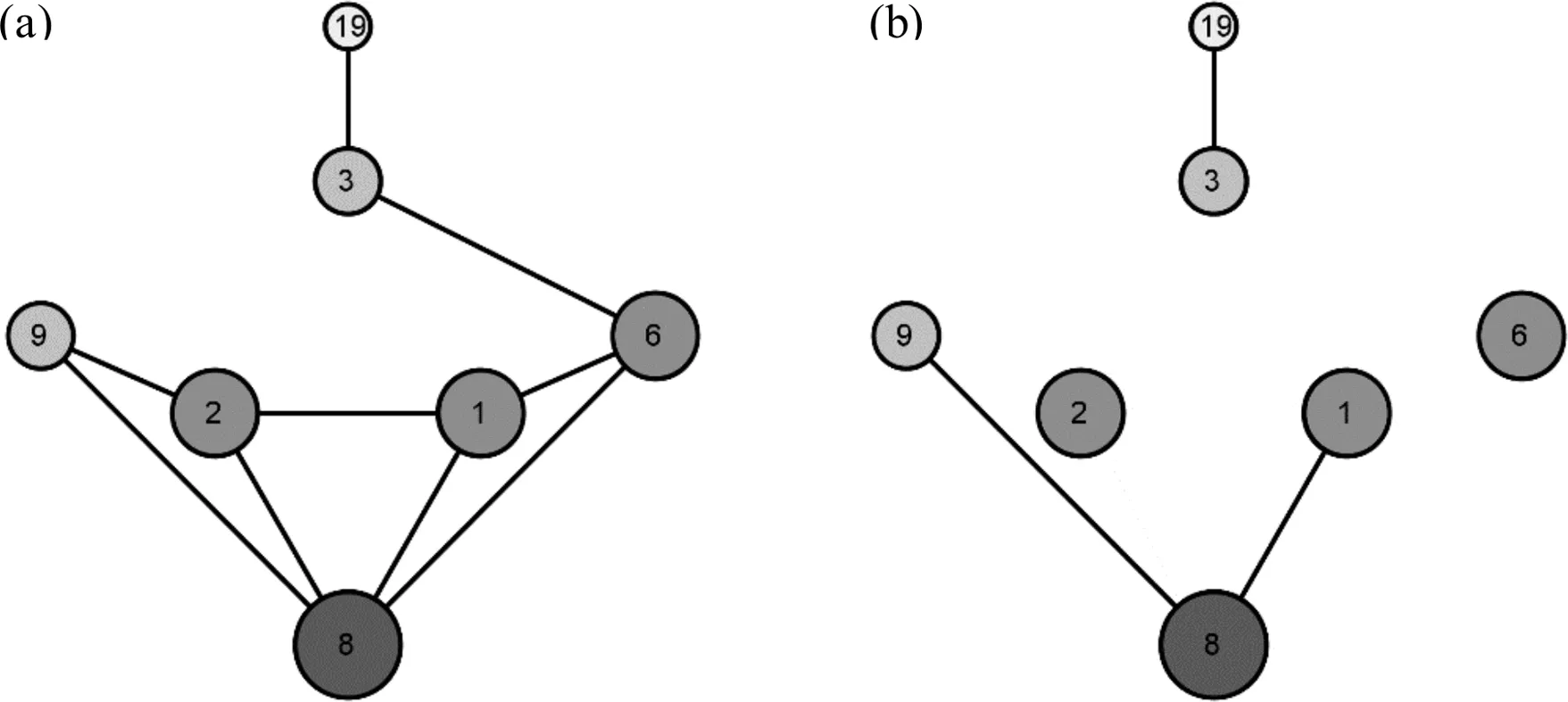
图8 网络A和网络B度排行前7的节点连接状况

网络舆情信息在网络A和网络B中的扩散效果如图9所示。从中可以看出，舆情信息在网络A中的传播比高于网络B，并且在系统趋于稳定时，网络A的知情比要高出网络B约20%。在舆情信息扩散的速度上，网络A同样明显高于网络B，虽然系统达成稳定所耗时长相差不大，但是，网络A中的舆情信息平均每一时步新增的知情者数量高出网络B约0.77。因此，网络舆情信息最终的扩散程度和平均扩散速度对网络结构上的富人俱乐部效应具有敏感性，富人俱乐部效应越强，网络中的富节点越倾向于彼此连接，从而提高了网络舆情信息的知情比和平均扩散速度[7]。

图9 富人俱乐部系数对网络舆情信息扩散的影响

4.3 初始传播者对网络舆情信息扩散的影响

初始传播者的数量和位置皆会影响网络舆情信息扩散效果。设网络舆情信息扩散的发生网络为κ=3、规模N=500的BA无标度网络，模型各参数的取值分别为λ=0.2，γ=0.15，M=3；分别令初始传播者数量I(0)取值为1、2、5、10和20，将实验重复50次并取其均值以消除随机性对扩散过程的影响，可以得到如图10所示的结果。从中可以看出，在设定的I(0)取值空间中，随着I(0)的增大，网络舆情信息最终的知情比越高，当I(0)≥10时，网络中只有很少的个体处于非知情状态(当I(0)=10时，z(200)=0.9504；当I(0)=20时，z(200)=0.9640)；在系统趋于稳定前，传播比随着I(0)的增大而呈现出越为陡峭的峰形，网络舆情信息扩散的瞬时速度也相对越高。从整体的趋势来看，随着初始传播者数量的增加，系统达成稳定耗时越短，平均每一时步增加的知情者(包含E、I、R三种状态的个体)数量越多，这表明初始传播者数量确实对网络舆情信息扩散具有显著影响。

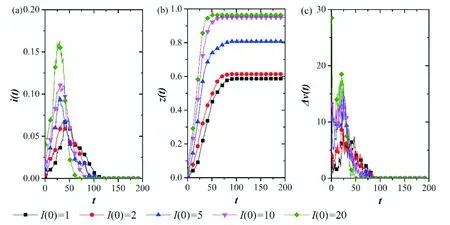
图10 初始传播者数量对网络舆情信息扩散的影响

沿袭上述BA无标度网络及模型参数，设定初始传播者数量I=1，分别令初始传播者度值ki等于3、5、10、20和47，3和47分别是网络的最小度值和最大度值。分别重复实验50次并取其均值可以得到如图11所示的结果。Moreno等人对非均匀网络中谣言扩散的研究结果表明，谣言的最终感染者数量R(t)与感染概率有着紧密关系，而与传播源的度ki无关[21]，这与一般意义上的传播过程是迥然不同的，因为传播源的度值直接关系到与之连接的个体数量，并进而对最终受感染人数产生影响。节点度值构成了节点网络结构熵的基本要素，它反映了各节点在网络中的重要程度，因而是衡量节点在网络中位置重要性的最主要指标[7]。如图11所示，初始传播节点度值越大，网络舆情信息的传播比曲线越呈现出陡峭的峰形，最终知情比也越高；网络舆情信息扩散瞬时速度的峰值越高，平均扩散速度越快；此外，受到最终知情比所表现出的显著差异的影响，系统达成稳定所需要的时间不具有线性趋势。因此，网络舆情信息扩散效果对初始传播者在网络中的位置具有敏感性，按照Burt等人的观点，“位置即资本”[14]，初始传播者在网络中占据的位置能够深刻影响网络舆情信息的扩散效果。

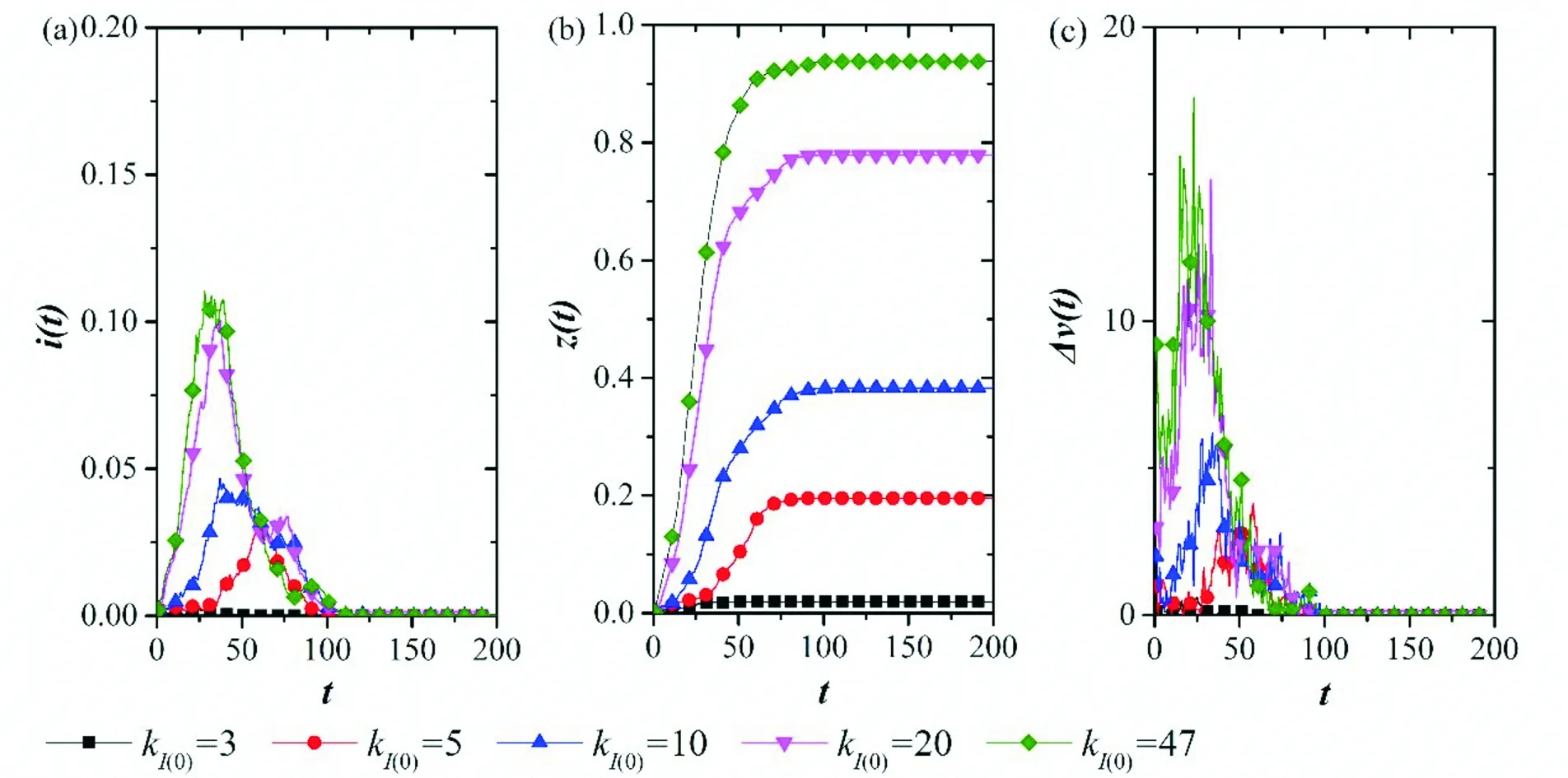
图11 初始传播者位置对网络舆情信息扩散的影响

5 结论

网络舆情信息的扩散本质上是发生在互联网空间中的信息流动过程，而互联网空间明显具有复杂网络的拓扑结构，为此，本文结合网络舆情信息扩散中的个体状态转移特性，构建了基于近邻响应的SEIR网络舆情信息扩散模型。通过对比传统的SEIR模型，本文构建的模型可以更好地拟合网络舆情信息扩散过程中不同类型个体的变化趋势。从网络类型、网络规模、网络平均度和网络富人俱乐部系数四个方面的实验表明，网络结构对网络舆情信息扩散效果具有显著影响；初始传播者的状态在网络舆情信息扩散过程中具有重要意义，从具有不同初始传播者数量和位置两个层面进行的实验表明初始传播者数量越多、位置越重要，网络舆情信息扩散效果越显著。

上述结论有助于我们更好地认知网络舆情的发展演化规律，在网络舆情治理过程中，不仅要明确网络舆情信息的性质，还要根据网络舆情发生场域的空间关系结构及初始传播者的属性特征实施有针对性的干预行为，这样才能更好地遏制网络谣言等虚假信息的传播，进而达成习近平总书记所说的“把握网上舆论引导的时、度、效，使网络空间清朗起来”。