空间机械臂可见光测量相机参数标定技术研究

谭启蒙 贾馨 陈磊 张运 蔡铮



空间机械臂可见光测量相机参数标定技术研究

谭启蒙1贾馨2陈磊1张运1蔡铮1

（1 空间智能机器人系统技术与应用北京市重点实验室，北京空间飞行器总体设计部，北京 100094） （2 北京空间机电研究所，北京 100094）

空间机械臂可见光测量相机参数标定是制约空间合作目标三维位姿测量精度的关键技术和重要前提，它直观表征了视觉标记三维坐标与对应的二维图像坐标之间正确的映射函数。针对现有相机内外参标定方法操作步骤繁琐、积累误差大、标定精度低等工程问题，文章提出一种空间机械臂可见光测量相机内外参标定方法，引入高精度二维棋盘格标定靶与基准镜共同作为转换中介，且在相机有效观测视场内随意移动标定靶，分布式解算相机内参和外参。试验表明，相机内参离散度均不超过±0.3像元，角点重投影误差均不超过±0.5像元；外参六自由度分量标准差均不超过（0.6mm，0.05°）。上述标定方法具有较强的可操作性，极大简化了坐标转换计算复杂性，有效降低了标定过程中产生的积累误差，为机械臂实施视觉闭环自主捕获合作目标提供了可靠依据。

可见光测量相机 内外参标定 平面标定靶 基准镜 空间机械臂

0 引言

近年来，伴随着人工智能技术的异军突起，空间机械臂[1]已经逐步发展成为航天科技领域不可或缺的重大关键技术之一，尤其是对在轨服务、深空探测等方面具有举足轻重的研究意义。截止目前，国外成功案例主要包括：加拿大航天飞机遥操作机械臂SRMS[2]、加拿大国际空间站遥操作机械臂SSRMS[3-4]、欧洲臂ERA[5]、日本实验舱机械臂JEMRMS[6]、日本试验卫星机械臂ETS-VII[7-9]和美国“轨道快车”机械臂[10]等，主要完成舱段对接、货物搬运、设备拆装、辅助航天员出舱、国际空间站在轨建设等。

相比于以往各类航天器携带的多种载荷相机，机械臂可见光测量相机[11]（简称相机）不仅兼顾监视、观测功能，还新增了对空间合作目标[12]进行目标检测识别以及三维位姿测量功能，为机械臂末端机构完成目标捕获提供可靠依据。内外参标定技术作为目标位姿测量的重要环节之一，其关键在于准确获取表征相机光学成像模型的内部参数以及描述相机与末端之间相对位置的外部参数，这是实现目标位姿精确测量的基本前提和重要保障。

传统的内外参标定技术将内参标定与外参标定划分为两个独立的部分。内参标定方面，加拿大遥操作机械臂SRMS视觉系统SVS（Space Vision System）提出一种基于圆型标记点阵列图案靶标的相机内方位元素标定方法[13-14]，该方法具有较高的标定精度，但计算过程繁琐，容易引起参数解的不稳定性。欧洲臂ERA[15]对比分析了栅格型、棋盘格型、圆点阵列型等多种靶标图案设计，指出棋盘格型标定靶设计标定结果明显优于其他图案设计。

外参标定的关键是选用何种坐标转换基准，妥善构建相机透镜组三维光学坐标系与机械臂末端三维结构坐标系之间的映射函数。加拿大的SRMS/ SSRMS以及专用灵巧臂SPDM等关键机构表面均粘贴若干圆型标记[16]，标记点直径占据相机视场约10~15个像元，粘贴厚度约1mm，且选用一种双层结构的特殊材料：上层是二氧化硅，下层是镍铝合金。一方面，利用经纬仪等精密测量仪器精测各标记点在不同结构坐标系下的三维坐标值；另一方面，利用相机观测上述标记点，精确测算出其在相机坐标系下的三维坐标值。然而，上述方式往往对标记材料、胶粘工艺等环节要求很高，以确保标记自身基准不变性。由于国内在材料研制、胶粘工艺等环节仍与国际先进水平存在一定差距，往往导致加工链路中产生较大误差而难以消除。

针对传统相机内外参标定技术存在的操作步骤繁琐、积累误差大、标定精度低等工程问题，本文提出了一套空间机械臂可见光测量相机内外参标定方法，利用黑白棋盘格图案的高精度二维标定靶与基准镜相结合共同作为坐标转换中介，代替国际空间站普遍采用的高精度标记点，还可在相机有效观测视场内随意移动标定靶，利用经纬仪等精测设备作为精测基准，分步解算表征相机成像模型的内参及其相对于机械臂末端的外方位参数。

1 基于可见光测量的机械臂捕获目标位姿测量原理

图1为机械臂末端执行器表面固定安装可见光测量相机示意，空间合作目标表面安装有已知棋盘格图案特征的视觉标记。

图1主要涉及4个坐标系：相机坐标系（C-CCC）以相机光心C为坐标系原点，C轴表示像平面水平坐标轴，正方向指向左侧，C轴表示像平面垂直坐标轴，正方向指向上方，根据右手定则，C轴为相机光轴，正方向指向外侧；基准镜坐标系（M-MMM）以基准镜中心M为坐标系原点，规定M轴平行于相机坐标系C轴，且二者正方向一致，规定M轴平行于相机坐标系C轴，且二者方向一致，M轴则由右手定则确定；末端执行器坐标系（E-EEE）和目标坐标系（W-WWW）定义方式与之完全类似，这里将不再赘述。

式中为表征相机光学成像模型的内参矩阵，包括有效焦距、主点坐标、畸变系数等；CW和CW分别为旋转矩阵和平移向量，客观描述了目标坐标系相对于相机坐标系之间的位姿关系；（，）主要通过对采集图像信息进行亚像元图像特征点中心定位算法检测得到；[W，W，W]T通常利用第三方精密测量仪器精测得到。

为使机械臂末端执行器能够准确捕获到合作目标，需要精确估计末端执行器坐标系与目标坐标系之间准确可靠的相对位置关系，计算公式为

式中EW，EW，EM，EM，MC，MC分别表示末端执行器与目标、末端执行器与基准镜、基准镜与相机之间的坐标系转换关系。其中，EW，EW是最终待求解未知量，其结果可直接用于引导机械臂末端执行器逐步靠近目标实施精确捕获；末端执行器与基准镜之间的相对位置关系EM，EM由三坐标测量机等第三方精密仪器预先精测得到，视为已知常系数；而MC，MC构成相机外参，表征基准镜坐标系至相机坐标系之间的相对位置关系。

2 相机内外参标定

相机内外参标定技术主要解算以下两项参数：

1）表征相机光学成像模型的内部矩阵；

2）表征相机与末端之间相对位置的外部参数，主要涉及MC，MC。

图2为相机内外参标定布局示意。

结合图2所示，相机内外参标定方法主要包括以下步骤：

其中，电子经纬仪三维测量系统坐标系T-TTT定义以其中两台经纬仪瞄准连线中点T为坐标系原点，规定T轴平行于基准镜坐标系M轴，且二者正方向一致；规定T轴平行于基准镜坐标系M轴，且二者方向一致；T轴则由右手定则确定。

步骤二，图2中P-PPP为平面标定靶坐标系，顺序选取标定靶黑白棋盘格图案中的6个红色十字角点并记录各点在标定靶坐标系下的坐标值（Pi，Pi，Pi）T，（=1，2，3，…，6）；规定平面标定靶坐标系P-PPP以棋盘格左上角十字格点P为坐标系原点，规定P轴平行于基准镜坐标系M轴，且正方向竖直向下；P轴平行于基准镜坐标系M轴，且正方向水平向右；P轴则遵循右手定则。

步骤三，保持相机固定不动，代入相机视场角计算相机最远距离处的最大观测范围，由于上述标定靶尺寸难以覆盖相机最大观测范围，就需要将相机观测视场进行划分，见图3。将标定靶沿P轴方向依次移动至若干指定的标定位置，确保能够覆盖最近、最远位姿测量距离；针对图3中的每个视场区域，标定靶顺序摆放7种姿态（见图4），分别为正视（标定板平面与相机光轴垂直）、向左偏摆（约30°）、向右偏摆（约30°）、向前倾斜（约15°）、向后倾斜（约15°）、向左旋转（约45°）、向右旋转（约45°）；

步骤四，当标定靶固定在某一位置姿态处，执行以下操作：

1）使用经纬仪顺序观测标定板中的红色十字角点，精确测得每个十字角点在电子经纬仪三维测量系统坐标系中的三维坐标值（Ti，Ti，Ti）T，（=1，2，3，…，6）；

2）根据步骤一的精测旋转矩阵MT和平移向量MT，计算出各红色十字角点分别在基准镜坐标系下的坐标值（Mi，Mi，Mi）T，（=1，2，3，…，6）；

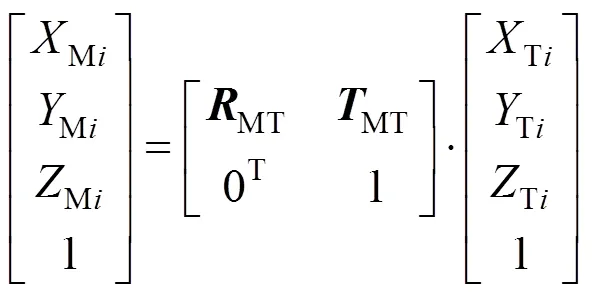
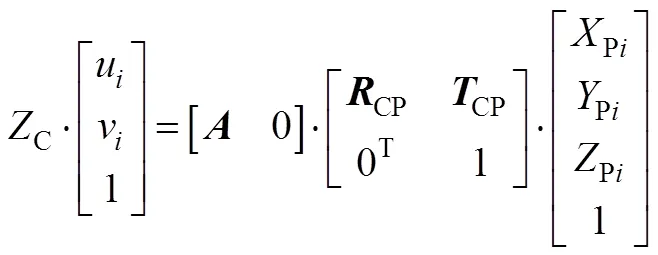
4）根据上述旋转矩阵CP和平移向量CP，计算出各红色十字角点分别在相机坐标系下的三维坐标值（Ci，Ci，Ci）T，（=1，2，3，…，6）；

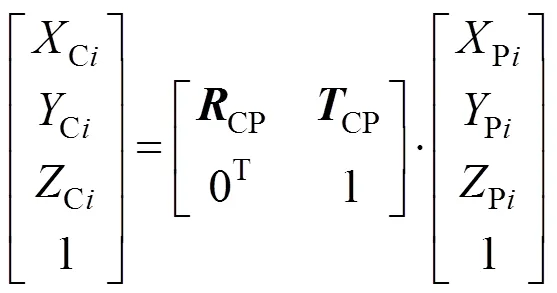
5）结合步骤2）和步骤4）的计算结果，利用SVD（Singular Value Decomposition）分解法[17]，计算出从基准镜坐标系至相机坐标系之间的旋转矩阵MC和平移向量MC；

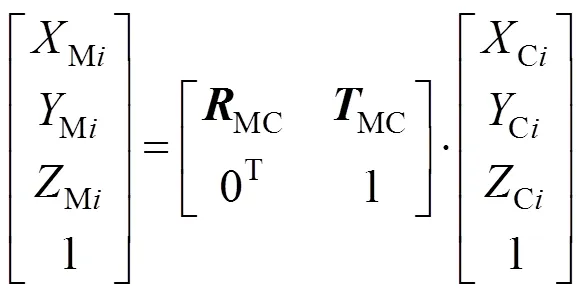
并转换成三个位置量{t，t，t}和三个旋转角{，，}等六自由度表示形式

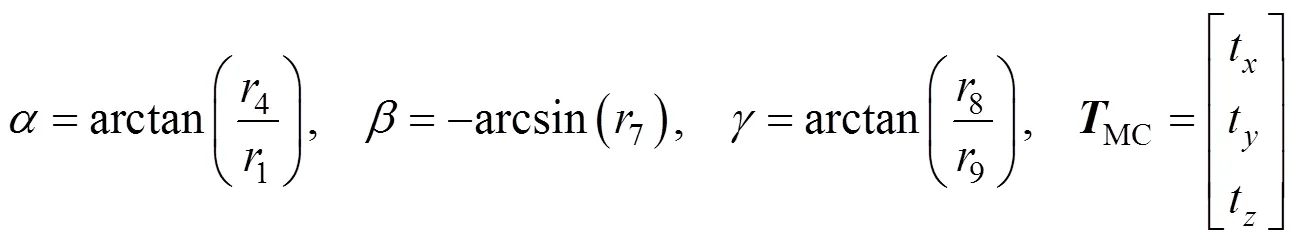
式中，，分别为基准镜坐标系M-MMM绕M轴、M轴、M轴的旋转角，旋转角正方向规定围绕各坐标轴逆时针旋转方向（遵循右手定则，拇指指向坐标轴正方向）；

步骤五，重复执行步骤三、四操作，直至标定靶沿P轴方向依次移动至全部标定位置为止，完成下列操作：

1）利用基于黑白棋盘格图案的平面靶标定方法[18-19]，分别计算得出相机的等效焦距、主点坐标以及畸变系数（含三阶径向畸变、二阶切向畸变）等内参；

3 试验结果与分析

实验室环境下，基于MATLAB软件仿真平台，对空间机械臂末端执行器固定安装的可见光测量相机开展内外参标定试验，主要目的是：

1）求解等效焦距、主点坐标和畸变系数等相机内参；

2）求解从基准镜坐标系至相机坐标系（M-MMMC-CCC）之间的转换关系，包括旋转矩阵MC和平移向量MC；

试验使用的平面标定靶黑白棋盘格的加工精度是0.05mm；采用3台Leica 5100电子经纬仪建立三维测量坐标系，建站精度为0.01mm，基准镜瞄准精度达0.02mm，则空间点位三维测量精度均优于0.04mm；用于改变平面标定靶位姿的六自由度调整机构的位置平移误差优于±0.5mm，姿态角度误差优于±0.1°。

试验过程具体如下：

1）在平面标定靶的黑白棋盘格图案中，人为选定涵盖棋盘格最大外包络且对称分布的6个十字角点标记为红色，具体站位布局见图5。

2）沿相机坐标系C轴方向，预先定义相机外参标定测量工况依次为：300mm，500mm，700mm，900mm，1 100mm，1 300mm。

3）相机固定安装在光学气浮平台上的安装支架上，保持相机位姿不变，平面标定靶随6自由度调整机构移动至指定的测量工况处，相机实时采集标定靶图像，利用改进型Harris角点探测器准确提取所有十字角点的二维亚像元坐标值，基于黑白棋盘格图案的平面靶标定方法，分别计算得出的相机等效焦距、主点坐标以及畸变系数（含三阶径向畸变、二阶切向畸变）等内参标定结果，具体如表1所示。

表1 相机内参标定数据

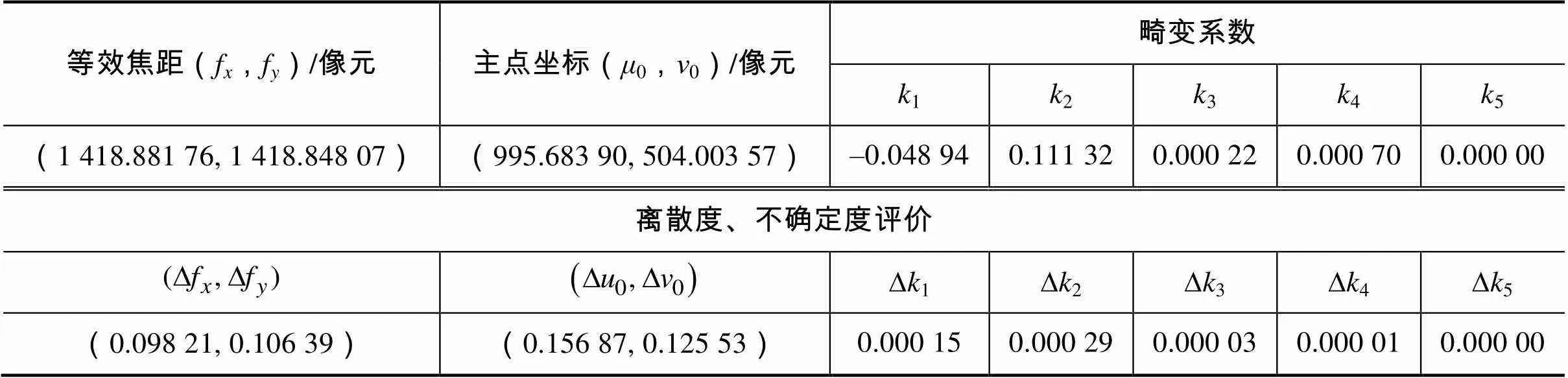
Tab.1 Experimental result for camera calibration of intrinsic parameters

4）标定靶中预先指定的各红色十字角点分别在标定靶坐标系、基准镜坐标系及相机坐标系下的三维坐标值，见表2。

根据表2数据，即可计算出相机在不同测量工况的外参结果，以6自由度形式表示，见表3。

5）将表3所列相机外参结果取平均值并代入式（7），即可作为相机外参标定结果。

表2 标定靶选取点在不同坐标系下的三维坐标

Tab.2 3D coordinates of 6 specified cross corners in different coordinate systems mm

表3 不同测量工况计算出的相机外参结果

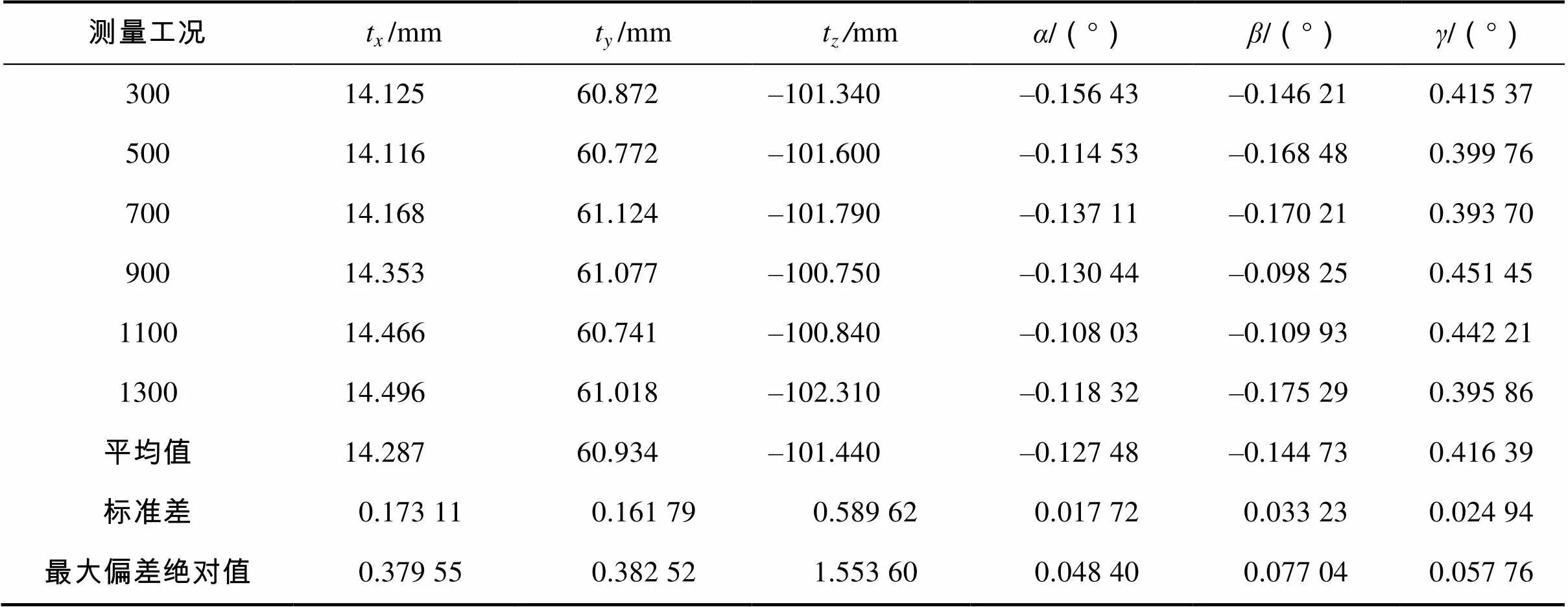
Tab.3 Calibrated results of extrinsic parameters calculated in different specified positions

经分析，表1列出的相机内参数据离散度均不超过±0.3像元，标定靶十字角点重投影误差均不超过±0.5像元，相机镜头畸变系数的不确定度均优于0.0003，可忽略不计；表3所列的相机外参6自由度分量标准差均不超过（0.6mm，0.05°）。该方法既能保证较高的标定精度，又能简化目标函数的计算难度，且具有很强的可操作性，极大地简化了多次坐标转换复杂性，有效降低计算过程中产生的积累误差，可使标定精度提高至少一个数量级。

4 结论

空间机械臂末端执行器配置可见光测量相机本质上都是对已知图案特征的视觉标记单帧图像，实时估计空间合作目标的三维位置姿态等信息。相机参数标定作为不可或缺的重要环节，标定结果将直接影响目标位姿测量的精度水平。为解决现有相机内外参标定技术存在的操作步骤繁琐、积累误差大、标定精度低等工程问题，本文提出了空间机械臂可见光测量相机内外参标定方法：内参标定借助一种包含黑白棋盘格图案的高精度二维平面靶，可在相机有效观测视场范围内任意运动（含平移、旋转等），分步计算表征相机成像模型的内参；外参标定，将黑白棋盘格平面靶与基准镜相结合共同作为坐标转换中介，引入第三方精测设备，求解相机坐标系相对于末端执行器的外方位参数。试验结果表明，相机内参离散度均不超过±0.3像元，角点重投影误差均不超过±0.5像元；外参6自由度分量标准差均不超过（0.6mm，0.05°）。上述标定方法具有很强的可实施性，精简了标定操作步骤，减小由多次坐标转换计算产生的积累误差，为机械臂实施视觉闭环自主捕获合作目标提供可靠依据。

[1] 林益明, 李大明, 王耀兵, 等. 空间机器人发展现状与思考[J]. 航天器工程, 2015, 24(5): 1-7. LIN Yiming, LI Daming, WANG Yaobing, et al. Current Status and Analysis of Space Robot[J]. Spacecraft Engineering, 2015, 24(5): 1-7. (Chinese)

[2] ASKER J R. Canada Gives Station Partners a Hand and an Arm[J]. Aviation Week & Space Technology, 1997, 147(23): 71-73.

[3] GRAHAM G, SACHDEV S. Canada and the International Space Station Program Overview and Status[C]//Montreal, Canada, Canadian Space Agency, 54th International Astronautical Federation (IAF). Bremen, Germany, 2003.

[4] SCOTT B N. Singularity Analysis of the Canadarm2[J]. Mechanics and Machine Theory, 2007, 42(4): 442-454.

[5] HEEMSKERK C J M, SCHOONEJANS P H M. Overview of the ISS large Manipulator Operations[C]//Proceedings of the Conference Engineering, Construction and Operations in Space. Albuquerque, NM, USA: ASCE, 1996.

[6] WOERKOM V, MISRA A K. Robotic Manipulators in Space: A Dynamics and Control Perspective[J]. Acta Astronautica, 1996, 38(4): 411-421.

[7] YOSHIDA K. Engineering Test Satellite VII Flight Experiments for Space Robot Dynamics and Control Theories on Laboratory Test Beds Ten Years Ago Now in Orbit[J]. International Journal of Robotics Research, 2003, 22(5): 321-335.

[8] FUKUSHIMA Y, INABA N, ODA M. Capture and Berthing Experiment of a Massive Object Using ETS-VII’s Space Robot: AIAA-2000-4537[R]. Washington, AIAA, 2000.

[9] ODA M, NISHIDA M. Space Telerobot Experiment System Based on NASDA ETS-VII Satellite: AIAA-97-3558[R]. Washington, AIAA, 1997.

[10] WILSON J R. Satellite Hopes Ride on Orbital Express[J]. Aerospace America, 2007, 45(2): 30-35.

[11] 陈磊, 高升, 袁宝峰, 等. 基于多相机的空间机械臂视觉系统[J]. 航天返回与遥感, 2014, 35(3): 35-42. CHEN Lei, GAO Sheng, YUAN Baofeng, et al. Multi-camera Based Space Manipulator Vision System[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(3): 35-42. (in Chinese)

[12] Committee on the Assessment of Options for Extending the Life of the Hubble Space Telescope, National Research Council. Assessment of Options for Extending the Life of the Hubble Space Telescope: Final report[M]. Washington, WA, USA: National Academies Press, 2005.

[13] MACLEAN S G, PINKEY H L. Calibration Procedures for the Space Vision System Experiment[J]. Proceeding of SPIE, 1991, 1526: 113-122.

[14] MAYBANK S. Camera Calibration of the KTH Head-eye System[R]. Technical Report CVAP 147, 1994.

[15] MACLEAN S G. Vision System Development in a Space Simulation Laboratory[J]. Proceedings of SPIE, 1990, 1395: 8-15.

[16] MCARTHY J. Space Vision System(SVS)[C]//Proceedings of 29th International Symposium on Robotics Automation and Robotics MACH'98 (Machine Tools) Control and Instrumentation. Birmingham, UK: DMG Business Media, 1998.

[17] ARUN K S, HUANG T S, BLOSTEIN S D. Least-squares Fitting of Two 3-D Point Sets[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1987, 9(5): 698-700.

[18] 谭启蒙, 胡成威, 高升. 空间机械臂视觉相机内参标定技术研究[J]. 航天返回与遥感, 2013, 34(6): 74-80. TAN Qimeng, HU Chengwei, GAO Sheng. Research on Calibration of Intrinsic Parameters for Space Manipulator Camera Based on 2D Planar Pattern[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(6): 74-80. (in Chinese)

[19] DONALD W M. An Algorithm for Least-squares Estimation of Nonlinear Parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431-441.

Study on Parameter Calibration of Photographic Camera with Visible Light for Space Manipulator

TAN Qimeng1JIA Xin2CHEN Lei1ZHANG Yun1CAI Zheng1

（1 Beijing Key Laboratory of Intelligent Space Robotic System Technology and Applications, Institute of Spacecraft System Engineering, CAST, Beijing 100094, China）（2 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

Parameter calibration is the key technique in measuring 3D pose of cooperative object by visible photographic camera for space manipulator, which can be used to represent a correct mapping function between 3D coordinates of visual target and its corresponding 2D image coordinates. The relateded coefficient matrix of characteristic parameters involves the estimation of intrinsic and extrinsic parameters calibration of photographic camera. To solve problems existed in the traditional calibrating technique, such as complicated operating steps, large accumulating error and poor accuracy, a novel approach is proposed by introducing a measuring reference combining a precise 2D planar target with a known checkerboard pattern and a datum mirror, which can accurately calculate intrinsic and extrinsic parameters step by step. Experimental results have shown that the standard deviation of intrinsic parameters lies in ±0.3pixel, with the re-projection error of corners not exceeding ±0.5pixel and the standard deviation of six degrees of freedom less than（0.6mm, 0.05°）. Accordingly, the proposed approach has obvious advantages at good maneuverability, fewer computing steps and smaller accumulating error, which can provide reliable 3D pose to assist space manipulator to capture the cooperative object.

photographic camera with visible light; calibration of intrinsic and extrinsic parameters; planar target; datum mirror; space manipulator

TP391

A

1009-8518(2018)05-0113-10

10.3969/j.issn.1009-8518.2018.05.015

谭启蒙，女，1982年生，2012年获北京邮电大学物理电子学专业博士学位，高级工程师。研究领域为机器人视觉、大尺寸3D测量及数字图像处理。E-mail：tanqimeng@foxmail.com。

2018-04-28

（编辑：王丽霞）