一种航天器位姿测量的鲁棒正交迭代法

张欢 王立武 唐明章



一种航天器位姿测量的鲁棒正交迭代法

张欢 王立武 唐明章

（北京空间机电研究所，北京 100094）

航天器位姿测量是许多空间任务和地面大型试验必不可少的关键环节，基于合作标志点的单目位姿测量技术是实现该测量的重要手段之一；由于受到外界复杂环境的干扰，标志点提取可能会出现野值点或者精度不一致的情况，传统的正交迭代方法对于该类问题不能够达到最优的求解精度，甚至求解错误。文章提出了一种基于M估计的鲁棒型正交迭代方法，使用M估计给每个标志点分配不同的权重，优化加权物方残差目标函数得到位姿参数。通过仿真验证和实物试验，证明了该方法可以较好地消除错误数据对测量的影响，提高了正交迭代算法的测量精度和鲁棒性。

位姿测量 正交迭代法 权值估计 鲁棒 航天器

0 引言

精确测量航天器的位姿是航天领域的一项基础技术[1-2]，是进行空间交会对接[3-4]、编队飞行[5]、太空机器臂[6]操作等空间任务不可缺少的前提，同时也是探测器缓冲着陆运动抛投实验[7]等地面验证试验的基础。近年来，由于光学相机体积小质量轻，基于图像的测量方法近距离测量精度高，因此基于单目相机图像的合作目标位姿测量技术在航天领域得到了深入的研究和应用。例如，美国的轨道快车项目在目标星上布置了角反射镜作为特征点，并在追踪星上安装了相机，相机对这些标志点进行检测后，使用合作目标位姿测量技术测得航天器之间的相对位姿[8]。

合作目标位姿测量技术利用人工布设在航天器上的特征光点或者是航天器本身具有的结构特征点，通过摄影测量可以求解得到航天器的位置和姿态参数。在摄影测量学中，使用个已知标志点的三维世界坐标以及二维图像像素坐标，求解世界坐标系相对于相机坐标系的问题，称为点透视算法（PnP）[9]。近些年，PnP问题研究得到了广泛的研究：第一个快速而高精度的算法是EPnP算法[10]，该方法通过最小化一个代数误差，可以快速解算位姿；直接最小二乘（DLS）算法[11]和OPnP方法[12]是可以快速、精确、能够处理多解情况的算法，它们使用多项式结式的方法得到残差的解析解，但往往提供了过多的可能解析解，且其中的绝大多数都不符合要求；UPnP方法[13]是一种能够同时处理中心投影模型和非中心投影模型的、线性复杂度的、并且是几何最优的算法；正交迭代（Orthogonal Iteration，OI）算法[14]是一种经典的广泛使用的迭代算法，与上述方法不同，该方法专门为了求解位姿估计问题而设计，具有精度高和计算速度快的优点，被广泛的应用于位姿测量领域。

近些年的PnP问题的求解着重在于提高求解速度和提高精度，而在航天领域中的位姿参数测量中还需要考虑算法的鲁棒性。这是由于太空环境中的强烈太阳光照或者是地面模拟试验环境中强烈灯光的影响，会导致图像出现过曝光现象。过曝光将大大降低标志点的提取精度，甚至得到错误的标志点图像坐标，即出现野值点。以上的介绍的EPnP、DLS和OI等PnP方法本质上是求解最小二乘问题，并且它们均假设每个标志点的提取精度一致，这不符合实际中野值点测量误差远大于普通标志点测量误差的事实。因此在存在野值点的情况下，上述PnP方法均不能够得到较好的位姿参数测量结果。

为了克服以上的困难，提高PnP算法鲁棒性，本文采用了鲁棒估计技术中的M估计[15]对正交迭代方法进行改进。其关键思想是通过赋予每个标志点不同的权重来改进优化经典正交迭代方法的目标函数，选择能使该目标函数达到最小值的位姿参数作为输出参数。权值的选择使用了鲁棒估计技术中的M估计，该方法可以自动地估计每个标志点的提取精度，精度越高赋予的权值越大；对于野值点，则赋予零权值。最终消除野值点与测量误差较大的点对位姿参数的影响，使得改进后的正交迭代法在保证计算精度的同时，也具有了较强的鲁棒性。

1 经典的正交迭代方法

为了使用正交迭代方法测量航天器位姿，需要在目标航天器上布置标志点，并建立一个与目标航天器固连的坐标系，称为世界坐标系，此外还需要在追踪航天器上或者是实验场中布置一台相机，用于获得标志的图像，并建立一个相机坐标系[16]。

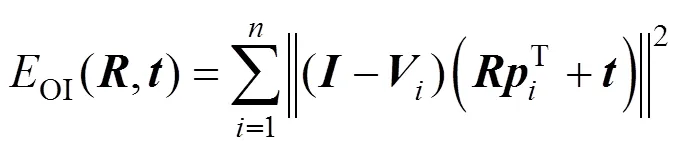
OI方法的基本思想是将求解旋转矩阵和平移向量的流程分开。在旋转矩阵已知的情况下，首先求解平移向量OI()使得目标函数OI(,)最小，

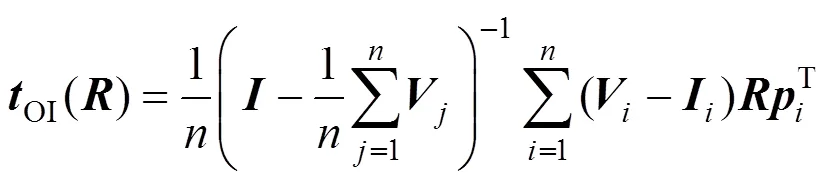
最后，使用求解绝对定向问题[17]的方法得到旋转矩阵。该流程可以循环往复，依次得到一系列的和，当位姿参数变化程度很小的时候停止迭代，输出和。

2 鲁棒正交迭代方法

从式（3）表示的优化目标函数中可以看出，该目标函数将所有的观测点数据都视为“平等”，即权值均相同。此时如果观测数据中存在野值点，该野值点必然会严重影响位姿参数测量。

为了克服野值点带来的影响，采用基于M估计的加权正交迭代算法以提高正交迭代算法的鲁棒性。该方法的基本思想是根据每一个标志点的提取精度，自动赋予以不同的权值。

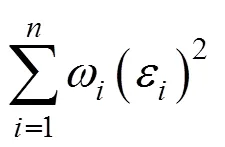
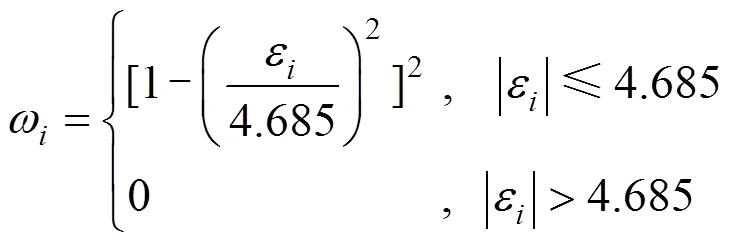
式中 阈值4.685由M估计方法给定[15]，该值的选取使得当残差满足标准正态分布时参数估计效果最优。

双权数函数的图像如图1所示，从图中可以发现，归一化残差的绝对值越大，权值越小。当归一化残差绝对值大于4.685的时候，认为该次的观测数据为野值点，赋予的权值为0，因而野值点数据不会影响加权物方残差函数，进而达到了剔除野值点对于位姿参数测量的影响。

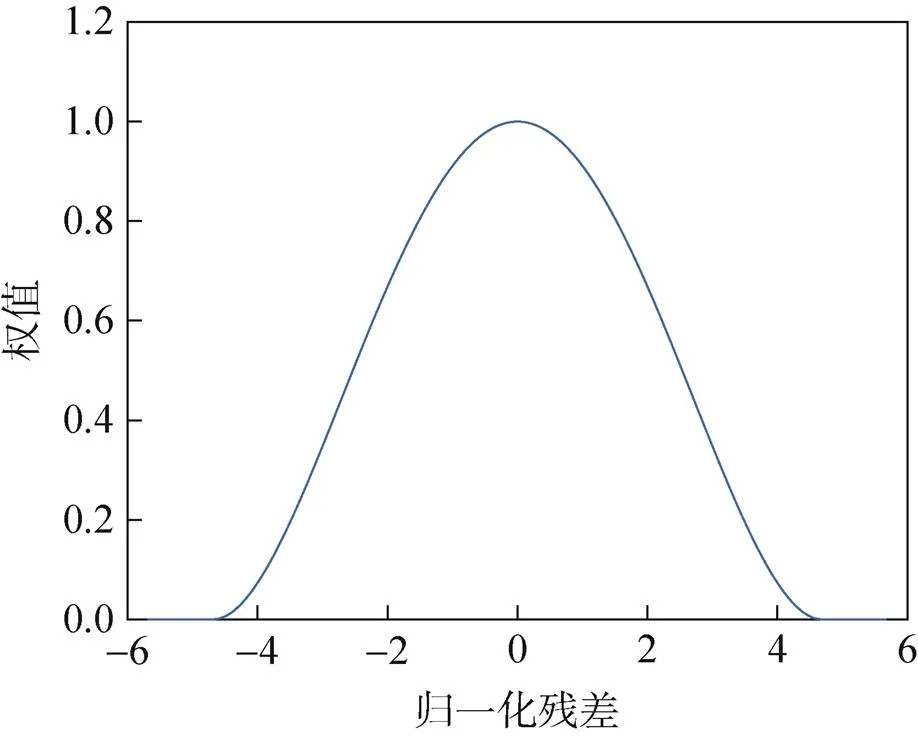
图1 双权数函数图像

权值确定之后，通过最小化加权物方残差函数可以求解得到位姿参数。首先将式（3）所示的目标函数进行加权，得到目标函数WOI(,)，即

式中WOI(,)为加权正交迭代算法（Weighted Orthogonal Iteration，WOI）的目标函数；为第个标志点对应的权重，≥0，权值的选择是通过M估计自动计算得出。当旋转矩阵给定的时候，WOI(,)可写成

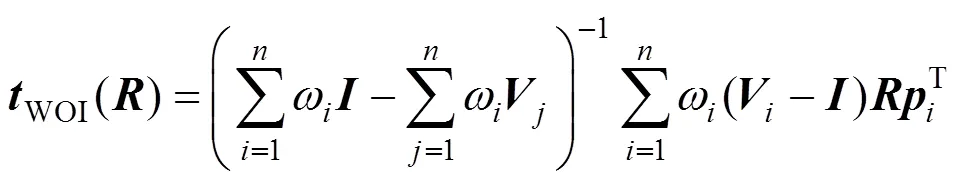
然后按类似于经典的正交迭代的流程，将旋转矩阵和平移向量依次使用迭代的方法进行求解。具体而言，首先分别计算()和的中心和，即

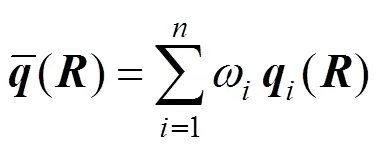
然后计算矩阵

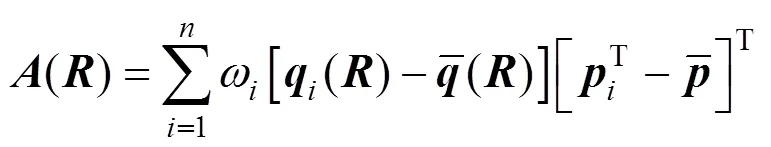
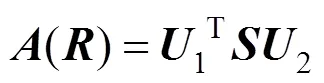
根据式（7）可以得到平移向量更新值(new)。如此循环往复，直到旋转矩阵和平移向量更新值稳定为止。

综合以上所述，鲁棒正交迭代算法步骤如下：

1）使用经典的正交迭代方法求解得到位姿参数初始值初始解(k)和(k)，其中表示迭代次数，初始时=0；

4）根据式（9）~（11）得到旋转矩阵更新值(k+1)，根据式（7）算得平移向量更新值(k+1)。

5）如果旋转矩阵和平移向量的变化量均小于给定阈值，则停止迭代，否则返回步骤2）。

3 仿真和试验验证

3.1 仿真试验

为了验证鲁棒正交迭代方法的有效性，利用Matlab进行了仿真验证，在计算精度和鲁棒性方面将其与传统的正交迭代方法进行对比。

为了与实验室实际使用的相机的内参数矩阵保持一致，仿真中采用的相机内参数矩阵为

由于实验室采用的中心投影相机，因此矩阵中方向和方向的等效焦距数值相同，光心图像坐标两个分量也相同。

每一次仿真中，随机生成旋转矩阵和平移向量。由于只有三个自由度，表示刚体绕三个轴的转角，可使用三维的罗德里格斯向量来等价表示。平移向量的、方向的分量t、t在[–100 mm，100 mm]内独立均匀分布，最后一个分量t选择为1 500 mm加一个[–250 mm，250 mm]间的均匀分布。仿真使用的标志点个数为12个，均匀分布在世界坐标系[–100 mm，100 mm]×[–100 mm，100 mm]× [–100 mm，100 mm]的立方体内。设置图像点的点位提取误差均值为0，方差为0.4个像素。为了测试鲁棒性，随机选择2个标志点的图像坐标，加入[0,50]像素的均匀分布噪声。根据仿真得到的罗德里格斯向量cal、平移向量cal，定义姿态的计算误差为D=cal–，平移向量的计算误差为D=cal–。仿真次数为15次。

为了方便显示，绘图时对姿态误差和位置误差进行了对数运算，图2分别给出了仿真的平移向量以及旋转矩阵的计算误差，表1为15次仿真试验的平移向量测量误差结果。从图2（a）以及表1可以看出，相比于经典的OI方法，本文提出的鲁棒正交迭代方法可以大幅度的提高平移向量的测量精度，有效克服了野值点带来的影响；由图2（b）以及表2可以看出，鲁棒正交迭代结果优于经典的正交迭代结果，可以有效地减少野值点的影响，提高测量精度，具有较好的鲁棒性。

在计算时间方面，由于需要额外进行权值的计算，鲁棒正交迭代法的运行时间要多于经典的正交迭代方法，鲁棒正交迭代方法需要的时间为0.04s左右，能够满足正常的航天器位姿测量的时间需求。

图2 经典正交迭代方法与本文方法的位置和姿态参数测量结果比较

表1 仿真试验中平移向量测量误差数据

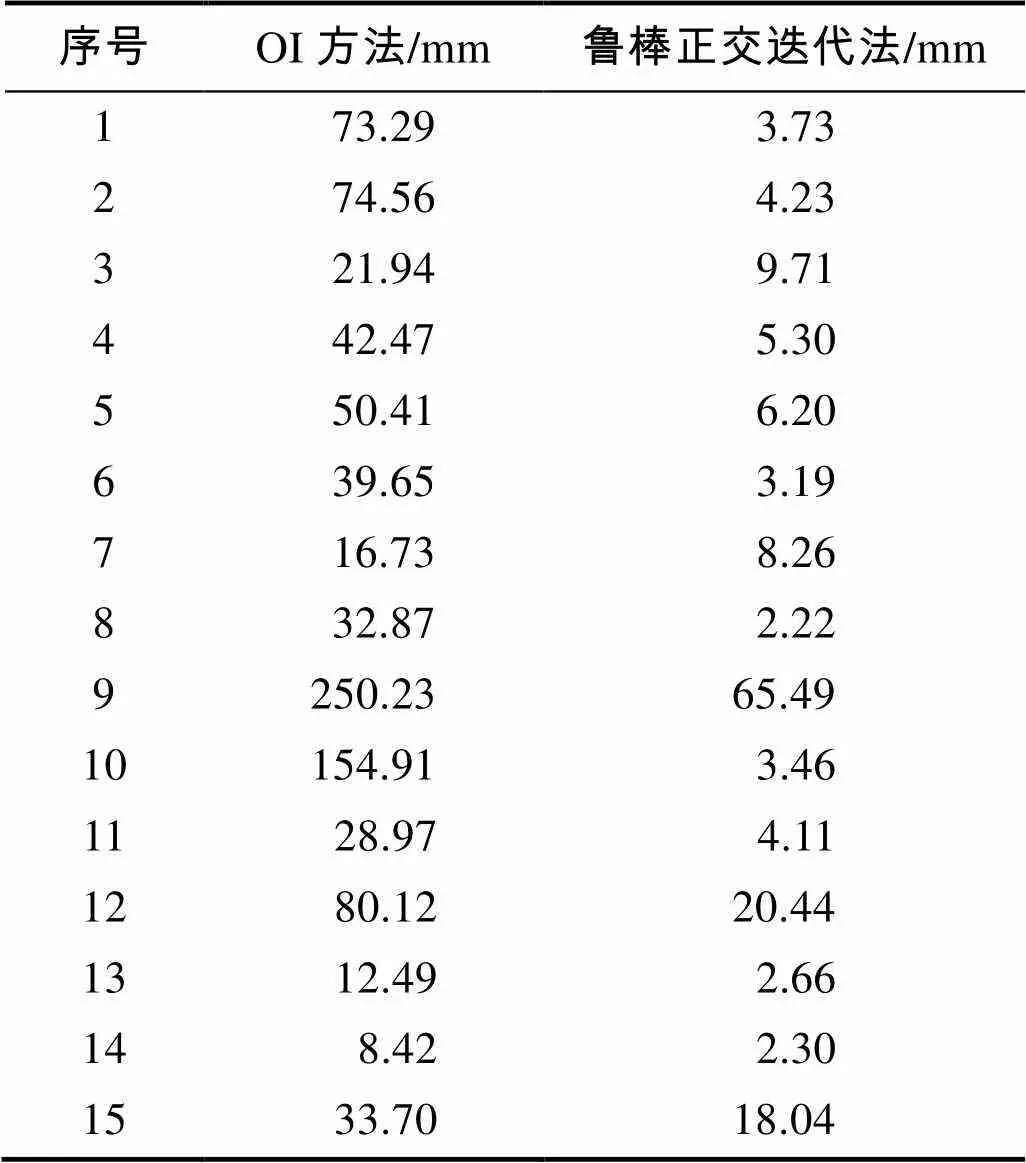
Tab.1 Translation vector measurement error data in simulation experiment

表2 仿真试验中姿态测量误差数据

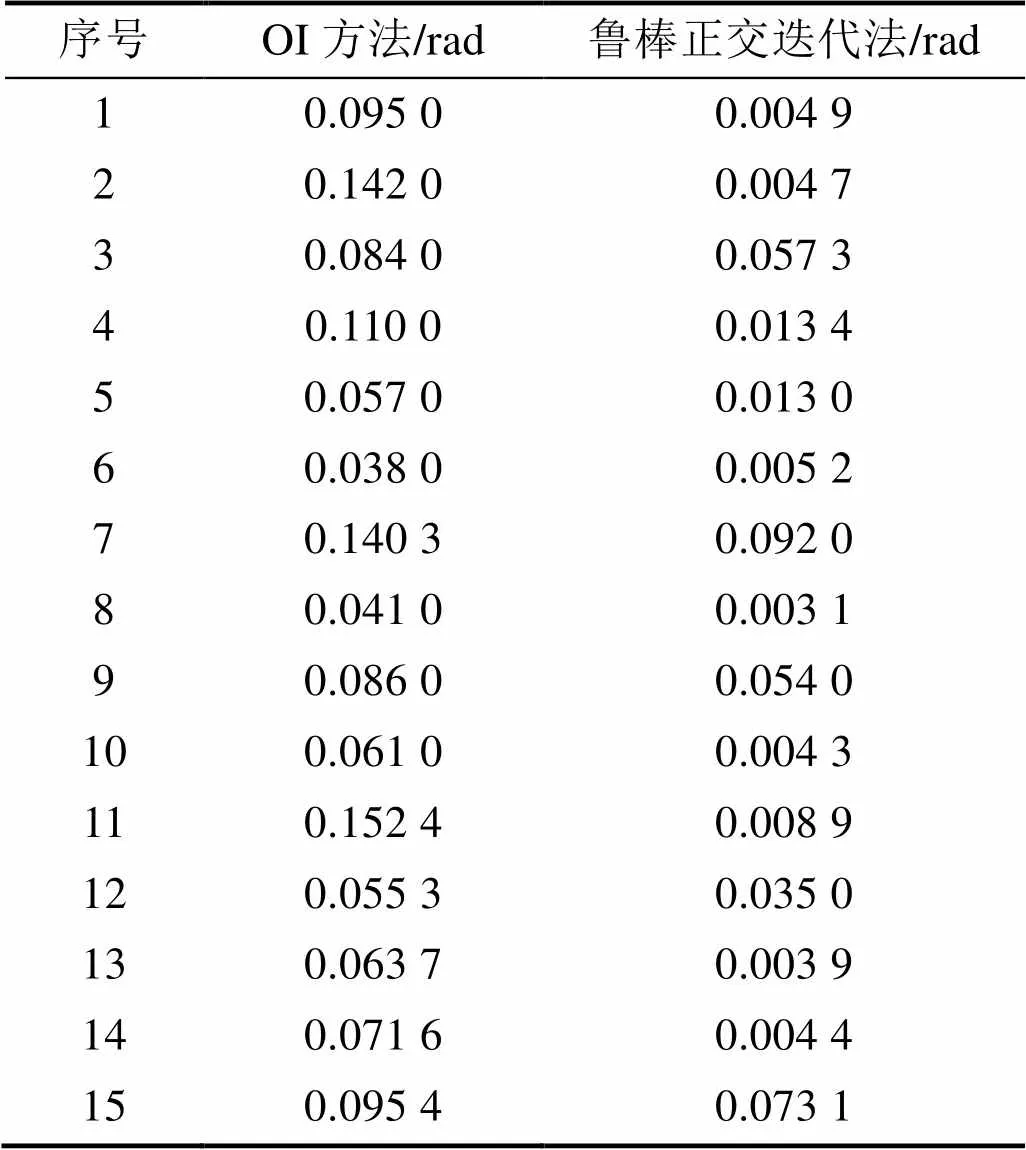
Tab.2 Attitude measurement error data in simulation experiment

3.2 实验验证

为了进一步验证鲁棒正交迭代方法的有效性，进行一组实物实验。实验装置由高精度控制平台和一台事先标定好内参数的相机组成，其中相机内参数使用张正友标定方法得到[18]。控制平台上固定了一块布置有若干标志点的铝板，世界坐标系固连在铝板上。标志点在世界坐标系中的坐标可以通过激光跟踪仪测量得到。由于世界坐标系到相机坐标系之间的旋转矩阵和平移向量难以直接测量，因此本文借助高精度控制平台移动世界坐标系，通过相机对标志点进行拍照，然后通过图像计算出前后两个世界坐标系相对于相机坐标系的位姿，进而计算出移动前后两个世界坐标系之间的位姿，将该位姿与高精度控制平台的结果进行对比，以此验证本文算法的鲁棒性。

在实验过程中，通过操作高精度控制平台，对铝板进行若干次平移，每次平移后，通过相机图像提取得到标志点的像素坐标。为了测试本文算法的鲁棒性，每次随机选择4个标志点的图像坐标，加入[0,50]的均匀分布噪声。将含有野值点的图像坐标代入本文鲁棒正交迭代方法，得到世界坐标系到相机坐标系之间的位姿参数，进而可以换算出两次平移之间的距离。将通过图像测量得到的平移量和控制平台输入的平移量进行对比即可验证本算法的鲁棒性。

实验数据如图3所示，其中图3（a）展示了实验中平移向量的测量误差结果；图3（b）展示了姿态参数的测量误差结果。可以看出，使用鲁棒正交迭代方法，能够有效克服野值点带来的影响，正确地进行位姿参数的求解。因此，本文提出的鲁棒正交迭代方法具有较好的鲁棒性。

图3 实验误差

4 结论

采用单目视觉系统对航天器位置姿态测量具有非接触、精度高、可靠性好、实施操作简单等特点，尤其在近距离范围内优势更为明显。为了提高经典的正交迭代算法的鲁棒性，本文基于摄影测量理论和鲁棒估计理论，提出了一种基于M估计的改进的鲁棒正交迭代算法。仿真与实验表明，相比于经典的正交迭代方法，该方法可以有效地克服野值点带来的影响，提高位姿解算的鲁棒性和计算精度。该方法可以应用于太空环境下的航天器位姿参数测量，也适用于地面的复杂光环境下的位姿参数测量，能够辅助完成空间交会对接、探测器缓冲着陆运动抛投实验等重大任务。

[1] 张庆君, 胡修林, 叶斌, 等. 基于双目视觉的航天器间相对位置和姿态的测量方法[J]. 宇航学报, 2008, 29(1): 156-161. ZHANG Qingjun, HU Xiulin, YE Bin, et al. Binocular Vision-based Relative Position and Attitude Determination Between Spacecrafts[J]. Journal of Astronautics, 2008, 29(1): 156-161. (in Chinese)

[2] 曹喜滨, 张世杰. 航天器交会对接位姿视觉测量迭代算法[J]. 哈尔滨工业大学学报, 2005, 37(8): 1123-1126. CAO Xibin, ZHANG Shijie. An Iterative Method for Vision-based Relative Pose Parameters of RVD Spacecrafts[J]. Journal of Harbin Institute of Technology, 2005, 37(8): 1123-1126. (in Chinese)

[3] 杜小平, 赵继广, 崔占忠, 等. 基于计算机视觉的航天器间相对状态测量系统[J]. 光学技术, 2003, 29(6): 664-666. DU Xiaoping, ZHAO Jiguang, CUI Zhanzhong, et al. Optical Method for Position-attitude Determination between Spacecrafts Based on Computer Vision[J]. Optical Technique, 2003, 29(6): 664-666. (in Chinese)

[4] 王保丰. 航天器交会对接和月球车导航中视觉测量关键技术研究与应用[D]. 郑州: 解放军信息工程大学, 2007. WANG Baofeng. Study on the Key Technologies of Computer Vision and Applications In RVD and Lunar Rover navigation[D]. Zhengzhou: Information Engineering University, 2007. (in Chinese)

[5] 徐文福, 梁斌, 李成, 等. 基于立体视觉的航天器相对位姿测量方法与仿真研究[J]. 宇航学报, 2009, 30(4): 1421-1428. XU Wenfu, LIANG Bin, LI Cheng,et al. The Approach and Simulation Study of the Relative Pose Measurement Between Space-crafts Based on Stereo Vision[J]. Journal of Astronautics, 2009, 30(4): 1421-1428. (in Chinese)

[6] 谭启蒙, 胡成威, 高升. 空间机械臂视觉相机内参标定技术研究[J]. 航天返回与遥感, 2013, 34(6):74-80.TAN Qimeng, HU Chengwei, GAO Sheng. Research on Calibration of Intrinsic Parameters for Space Manipulator Camera Based on 2D Planar Pattern[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(6): 74-80. (in Chinese)

[7] 晁志超, 姜广文, 黄伟, 等. 无人月球探测器缓冲着陆抛投试验视觉测量系统[J]. 光学精密工程, 2010, 18(9): 2044-2052.CHAO Zhichao, JIANG Guangwen, HUANG Wei, et al. Vision Measuring System for Soft-landing Drop Test of Unmanned Lunar Explorer[J]. Optics and Precision Engineering, 2010, 18(9): 2044-2052. (in Chinese)

[8] 徐文福, 刘宇, 梁斌, 等. 非合作航天器的相对位姿测量[J]. 光学精密工程, 2009, 17(7): 1570-1581. XU Wenfu, LIU Yu, LIANG Bin, et al. Measurement of Relative Poses between Two Non-cooperative Spacecrafts[J]. Optics and Precision Engineering, 2009, 17(7): 1570-1581. (in Chinese)

[9] 尚洋. 基于视觉的空间目标位置姿态测量方法研究[D]. 长沙: 国防科学技术大学, 2006. SHANG Yang. Researches on Vision-based Pose Measurements for Space Targets[D]. Changsha: National University of Defense Technology, 2006. (in Chinese)

[10] LEPETIT V, MORENO-NOGUER F, FUA P. EPnP: An Accurate O(n) Solution to the PnP Problem[J]. International Journal of Computer Vision, 2009, 81(2): 155-166.

[11] HESCH J A, ROUMELIOTIS S I. A Direct Least-Squares (DLS) Method for PnP[C]//IEEE International Conference on Computer Vision. IEEE, 2012: 383-390.

[12] ZHENG Y, KUANG Y, SUGIMOTO S, et al. Revisiting the PnP Problem: A Fast, General and Optimal Solution[C]//IEEE International Conference on Computer Vision, 2013: 2344-2351.

[13] KNEIP L, LI H, SEO Y. UPnP: An Optimal O(n) Solution to the Absolute Pose Problem with Universal Applicability[C]//Computer Vision-ECCV, 2014: 127-142.

[14] LU C P, HAGERG D, MJOLSNESS E. Fast and Globally Convergent Pose Estimation from Video Images[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2000, 22(6): 610-622.

[15] SUSANTIY, PRATIWI H, SRI S H, et al. M Estimation, S Estimation, and MM Estimation in Robust Regression[J]. International Journal of Pure & Applied Mathematics, 2014, 91(3): 349-360.

[16] 于起峰, 尚洋. 摄像测量学原理与应用研究[M]. 北京: 科学出版社, 2009.YU Qifeng, SHANG Yang. Videometrics: Principles and Researches[M]. Beijing: Science Press, 2009. (in Chinese)

[17] HORN BERTHOLD K P, HUGH M. Hilden and Shahriar Negahdaripour, Closed-form Solution of Absolute Orientation Using Orthonormal Matrices[J]. Journal of the Optical Society of America, 1988, 5(7): 1127-1135.

[18] ZHANG Z. A Flexible New Technique for Camera Calibration[J]. IEEE Transations on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334.

A Robust Orthogonal Iteration Method for Measuring the Pose of Spacecraft

ZHANG Huan WANG Liwu TANG Mingzhang

（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

Pose estimation of spacecraft is a key link indispensable for many space missions and large-scale ground tests. Monoclinic pose estimation based on cooperation points is one of the important means to realize this measurement. Due to the interference from complex environment, the sign point extraction may have outliers or inconsistencies in accuracy. The traditional orthogonal iteration method can’t achieve optimal solution accuracy and even obtain false solution for such problems. In this paper, a robust orthogonal iterative method based on M estimation is proposed, in which M markers are used to assign different weights to each marker point, and the residual objective function of weighted object is optimized to get the pose parameters. The results of simulation and experiment show that this method can eliminate the misdata influence on the measurement and improve the measurement accuracy and robustness of orthogonal iterative algorithm.

pose estimation; orthogonal iteration; weighted estimation; robustness; spacecrafts

O436；V19

A

1009-8518(2018)05-0066-08

10.3969/j.issn.1009-8518.2018.05.009

张欢，男，1987年生，2012年获南京理工大学军事化学与烟火技术专业硕士学位，工程师。目前主要从事航天器系统试验光学测量方面的工作。E-mail：491933842@qq.com。

2018-01-29

（编辑：夏淑密）