考虑加工余量的叶轮颤振稳定域预测分析

宋盛罡， 边立健， 冯闯

（1.中船重工鹏力（南京）智能装备系统有限公司，南京211106；2.温州职业技术学院，浙江温州325035；3.苏州斯莱克精密设备股份有限公司，江苏苏州215164）

0 引言

航空航天产业是国防制造业重要的组成部分之一，伴随着国家制造业的发展、大飞机项目的实施，对航空发动机的需求更是迫在眉睫，而叶轮是航空发动机的重要零部件，其制造加工周期长、材料去除率大、难度非常大。同时，叶轮的加工质量直接关系到整个装备的工作效率[1-2]。在叶轮加工过程中，由于其具有壁薄、刚度低、加工质量时变等特点，极易发生变形及振动，从而产生振纹，致使其加工精度往往难以保证。同时，叶轮等薄壁件加工振动问题由来已久，且影响因素复杂、形式多样，控制难度大，一直是业界研究的重点[3-5]。目前，已有众多学者针对此问题进行研究[6-8]，对加工系统进行颤振稳定域预测，选择适当的加工参数是避免发生颤振、提高加工质量的有效方法之一[9-11]。

本文针对叶轮加工过程中易出现的颤振现象，建立薄壁件动态铣削加工系统数学模型，进行铣削力系数辨识，并考虑叶轮加工过程中加工余量变化、刚度时变特点，对叶轮加工系统进行三维稳定域预测分析，为优化切削参数、避免颤振、提高加工质量、刀具设计提供必要依据。

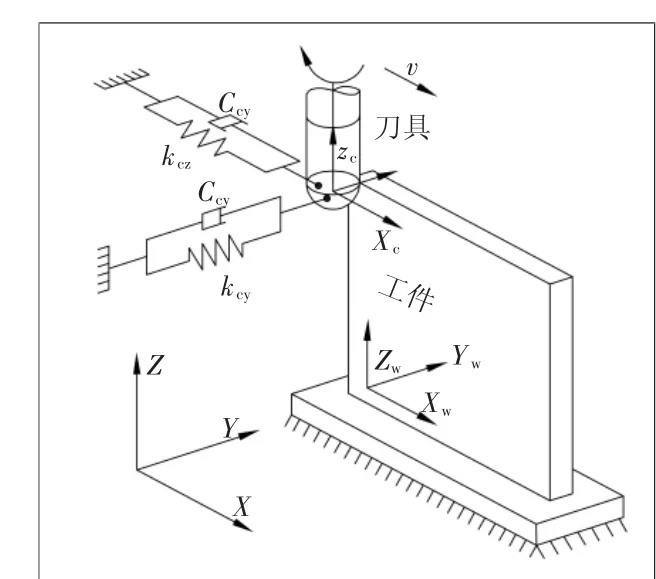
图1 动态铣削加工系统

1 铣削加工系统动力学建模

在薄壁件铣削加工过程中，随着加工过程的进行，工件的质量及刚度等都随之发生改变，此时二维稳定域往往不能客观、全面地将加工系统中稳定性的变化表达出来。因此，需要对颤振系统进行三维稳定域研究。

铣削加工系统模型如图1所示，其中OXYZ为参考坐标系，OccXcYcZc为刀具坐标系，OwXwYwZw为工件坐标系。

工件在铣削加工瞬间，其结构特性不会发生改变。此时，切削刀具的瞬时动态切削厚度hj（t）（考虑再生效应）可以表示为[12]：

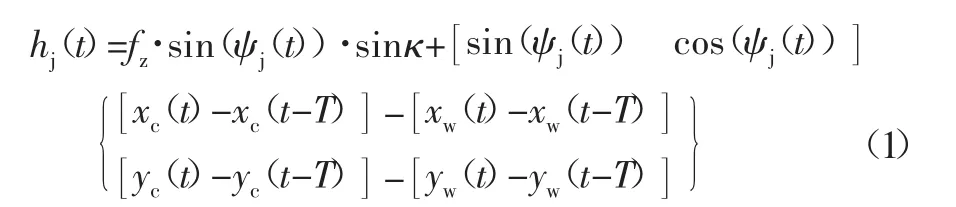
式中：fz为刀具每齿进给量；［xc（t）,yc（t）］T为刀具的位移量；［xw（t）,yw（t）］T为工件的位移向量；ψj（t）为示刀齿j的转角量，即

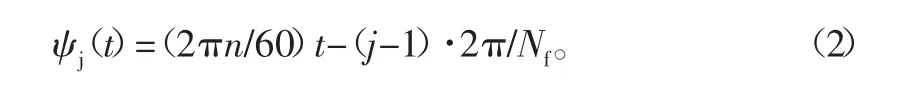
式中：Nf为刀齿数；n为转速。

在薄壁件铣削加工领域，工件Yw方向的刚度要远远小于工件Xw向的刚度，因此可不必考虑Xw向变形，则式（1）变化为

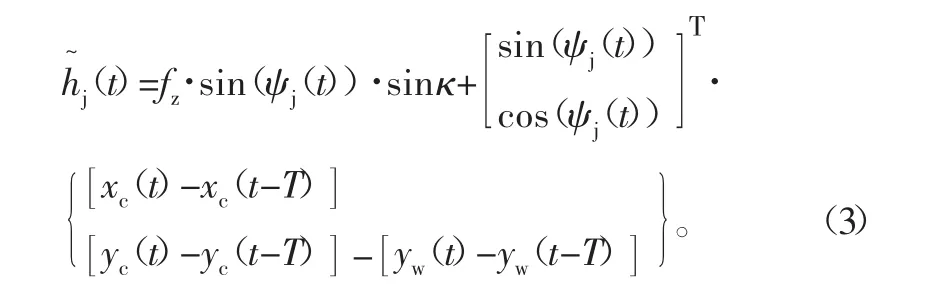
在铣削力研究方面，其基本铣削力数学模型[13]为：

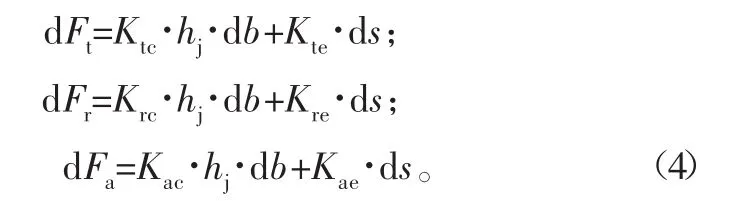
式中：dFt、dFr、dFa分别表示切向、径向、轴向铣削力微元；ds表示参与切削的切削刃长度微元。

那么，球头铣刀的瞬时切削力合力为

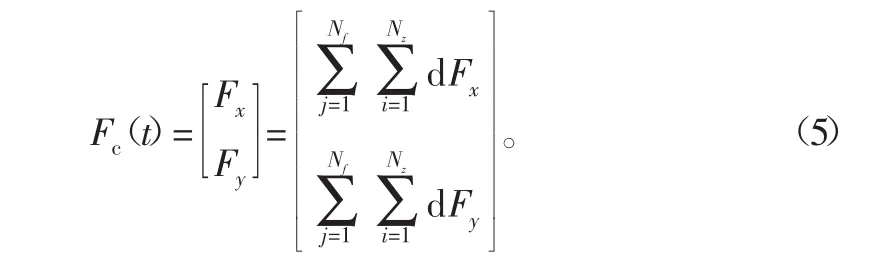
式中：Nz为第j条铣削刃铣削时参与铣削的微小单元数量；Fx和Fy为刀具受到的作用力。

当同时考虑工件及刀具的多模态效应，并将qx（t）和qy（t）为刀具在X、Y两方向上的模态坐标，同时都保留pc阶模态，此时的振型矩阵可表示为Px和Py，假设轴向切深相对较小，对铣刀的模态耦合进行忽略处理，那么铣削系统动力学模型的数学表达式[14]可表示为

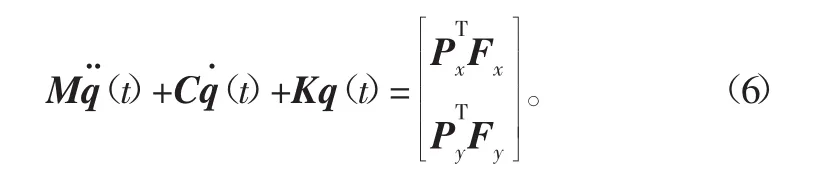
2 基于全离散法的颤振稳定域预测

全离散法具有较多优点，其中之一是计算效率高。使用类似于广泛运用于哈密顿系统中的变换式[15]，设p（t）=则式（6）可以转化为如下状态空间形式：

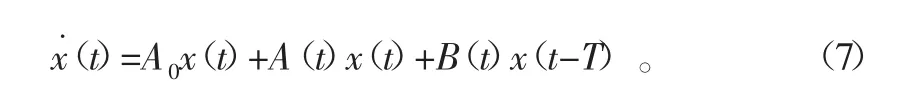
式中：

设刀具旋转周期T等同于时滞量，并将其等距离散，即T=mτ。根据精细积分法[16]，可得

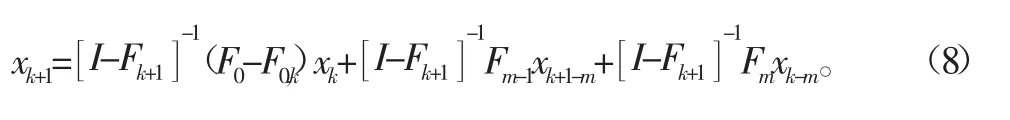
式中：yk=col（xk,xk+1,…,xk+1-m,xk-m）；

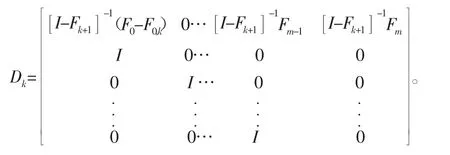
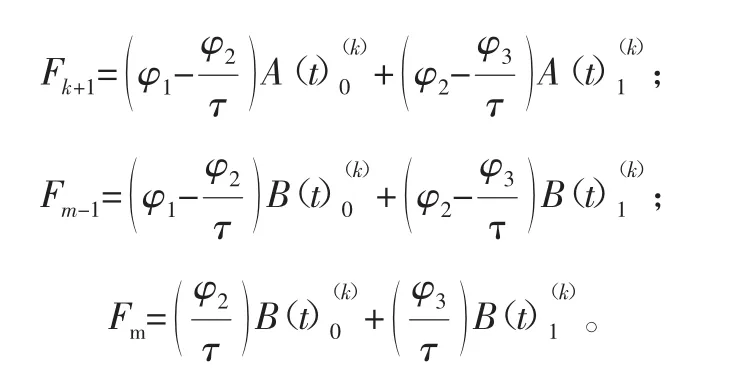
图2 刀尖点频率响应函数曲线

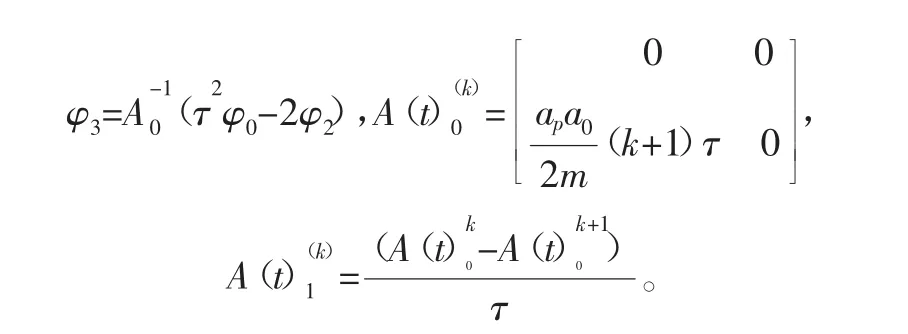
然后，系统在单个时间周期上的状态转移矩阵φ可以通过矩阵序列Dk，（k=0,1,…,m－1）构造出来，即yk+1=Dkky。

其中φ定义为φ=Dm－1Dm－2…D1D0。最后，根据Floquet理论，若转移矩阵φ的所有特征值的模均小于1，则系统稳定。

3 系统模态参数及铣削力系数识别

以MIKRON UCP710五轴数控机床、SANDVIK球头铣刀（R216.64-08030-AO09G 1610）为例建立模态实验系统，应用模态分析软件Cutpro对模态实验信号进行分析处理，即得到“机床-刀具”系统的FRF图形。优化拟合该“机床-刀具”系统的频响函数，即可得到相应的系统结构x向和y向的频响函数曲线，如图2所示。表1为“机床-刀具”系统的刀具（直径φ8）的等效模态参数。

表1 “机床-刀具”系统的刀具（直径φ8）等效模态参数

应用Gradisek[17]平均铣削力方法及模型识别铣削力系数。机床为MIKRON UCP710五轴数控机床，刀具为SANDVIK球头铣刀（R216.64-08030-AO09G 1610），实验工件为TC11。

实验采用干切削、不加任何冷却液、顺铣的加工方式。表2为铣削实验参数。

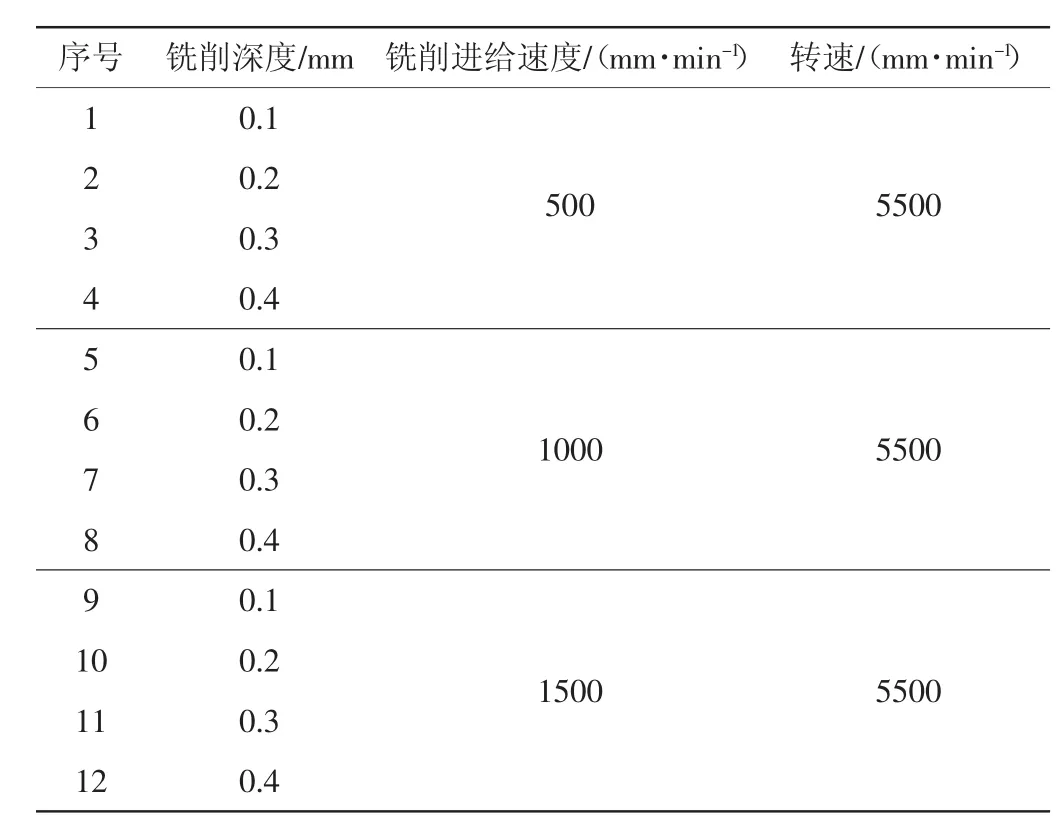
表2 实验参数

实验采用Kistler9257B测力仪；信号采集分析系统为东华DH5922；加速度传感器采用PCB，其灵敏度参数为10.42 mV/g；Kistler5007电荷放大器。铣削测试系统建立后，依次进行铣削加工实验，对测试数据计算得到平均铣削力。图3为铣削力系数测试系统原理图。

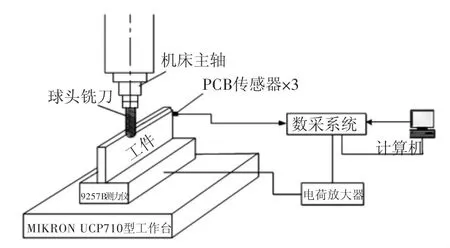
图3 铣削力系数测试系统

表3 TC11的铣削力系数 N/mm2

根据实验模型进行计算，计算结果如表3所示。

4 叶轮加工余量变化对颤振稳定域的影响

由于叶轮壁薄，加工过程易产生振动，难以保证加工质量，因此对叶轮进行颤振稳定域仿真，可有效指导加工，提高加工质量与效率。同时在叶轮加工过程中，叶片的加工余量会随时发生变化，因此考虑叶轮加工余量时变的特点，根据全离散法可计算出该铣削系统的颤振稳定域。图4为叶片加工过程中切削余量的变化图，叶轮加工余量由1.5 mm逐渐变化为无加工余量。

图4 叶轮铣削加工余量的变化

考虑叶轮加工余量时变的特点进行仿真，得到的铣削加工颤振稳定域的变化情况如图5所示，从图中可以发现随着时间参数的变化，铣削加工系统的稳定域发生了微小的变化。

5 结 论

颤振现象一直是叶轮加工过程中普遍存在的，加工过程中对颤振现象的抑制可有效提高叶轮的加工质量。本文建立了薄壁件动态铣削系统数学模型，并进行铣削力系数辨识，基于全离散法对叶轮加工过程进行三维颤振稳定域预测分析，得到：1）叶轮加工过程中随着加工余量变化，铣削系统的三维稳定域变化微小，铣削稳定性曲线有整体下移的趋势;2）叶轮稳定域的预测分析可能会与实际加工情况有一定的偏差，因为柔性加工系统是一个十分复杂的系统，基于现有条件不会考虑到所有的影响因素，同时颤振现象是一个极其复杂的问题，因此稳定域的确定会与实际加工过程有一定的偏差，但这种偏差是可以接受的。后续应加强对薄壁件动态铣削系统数学模型的研究，构造更准确的数学模型，这样可以更好地为叶轮加工的参数选择提供依据。