基于遗传算法的通信系统传输网络拓扑架构研究
2018-11-09夏文云马晓亮
王 琼,夏文云,马晓亮
(江苏第二师范学院 物理与电子工程学院,江苏 南京 210013)
0 引言
传输网络一般采用核心-汇聚-接入的三层结构,基于安全考虑,汇聚层面通常选择两个节点,接入层的其他宏基站采用双归的方式接入这两个汇聚节点,从而形成传输环路,实现对末端节点的业务收敛。这就要求网络拓扑的优化必须在满足遍历所有节点的前提下,降低整体建网成本,即占用管线长度和路由条数越小越好。这与著名的推销员旅行问题(Travel Saleman Problem or TSP)极其相似[1],即要求推销员遍历既定的城市,而使得总的路费开销最小。
传统方法多以经验为基础,通过简单的计算完成网络优化,但是这往往会牺牲网络的经济性。遗传算法模拟自然进化过程,是一种具有并行特征的搜索算法,利于对解空间进行搜索,加快对解的搜索速度,便于推广到多节点的网络优化设计中,是解决大规模网络优化问题的有效工具。
本文借助数学模型的思想[2],将传输网络的拓扑优化抽象为NP-Hard问题,并利用遗传算法,使得在满足覆盖和安全的前提下,整体建网成本最低。
1 NP-hard模型
NP是指非确定性多项式(non-deterministic polynomial,缩写NP)。所谓的非确定性是指,可用一定数量的运算去解决多项式时间内可解决的问题。传输网络采用核心-汇聚-接入的三层结构,其中,接入层最靠近末端节点,数量最多,结构也最复杂。传输系统的拓扑网络结构与TSP问题类似[3,4],是一个改进型的双点NP-hard问题,如图1所示,如何能够在满足双归和环上最多节点限定的条件下,环路总成本最低。

图1 传输系统接入层网络
在传输系统接入层网络中,每个汇聚子区内有两个汇聚节点,区域内的所有宏基站均采用双归的方式接入。在已知任意两个基站点之间的管线连接成本,以及限定每个接入环下挂宏站数量的条件下,要求整体建网成本最低,即管线成本和设备成本总和达到最低。图1中从A到B规划若干条路由遍历所有基站点,要求满足总成本最低,即管线长度最短且路由条数最少。其中限定条件为单条路由下挂点有上限,同一条路由不可重复经过同一段落。已知条件为任意两个基站点之间的管线连接成本已知。对区域内接入环结构最优的NP-hard问题进行数学建模,成为一个求函数最小值的优化问题。
本文通过对资管系统中的现网任意站点之间接入层光缆纤芯长度进行摸查,得到任意基站间的最短接入层纤芯长度矩阵表。同时,根据无线专业的站点规划选址库,对待建站址进行撒点,结合现有基站的分布确定任意基站间需要新建管线的新建光缆长度矩阵表。设备成本主要受环路数量影响,环路数量越多,对汇聚设备的端口占用越多,设备成本越高。
2 遗传算法
遗传算法(Genetic Algorithm)[5-7]是一类借鉴生物界的进化规律演化而来的随机化搜索方法。由于遗传算法采用随机运算,对搜索空间无特殊要求,无需求导,具有运算简单、收敛速度快等优点,因此近年来有很快的发展,并在组合优化、自适应控制、机器学习等许多领域获得应用。遗传算法流程如图2所示。
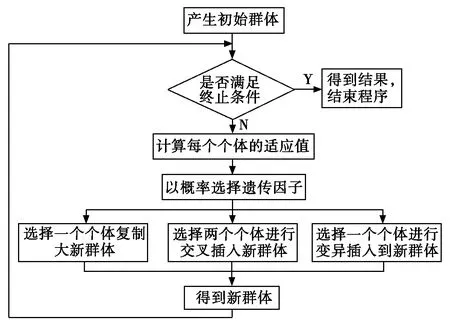
图2 遗传算法流程图
1) 建初始状态
首先,我们做一些基本处理:将所有1—N个点编号,起点为1号,终点为N号。计算各点两两间的相关度(即成本),用一组数表示,若完全不相关,则取相对较大的数,或者正无穷。
其次,要产生一组样本空间,步骤如下:
a) 生成一个样本的数组,用于存放路径以及每条路径经过的点,数组为二维,行存放一条路径经过的点的号码,列存放不同路径的信息。数组行数不大于N/MIN,列数不大于MAX。
b) 对于每条路径经过点的个数限制,我们用在MIN(环路最小节点数,取1)到MAX(环路最大节点数,取8)之间产生一组随机整数,以此作为每条路径所经过点的数目。
c) 对路径数以及每条路径经过的点数进行约束,即需要满足数组内的点包含所有N个点,当要求各点只能利用一次时,亦可以将数组调整为全部N个点的不重复随机排列。
d) 另设一份向量描述样本的信息,即路径的选择与长度等情况。
e) 以上可获得一份样本,重复a)-d)可得到一组样本空间,其中要检查避免各样本的相似性过大,以求获得较为全面的“基因库”。需要注意,样本空间中的样本数量需要根据实际情况调节,当问题复杂度较低时,样本数可取较少,当问题复杂度较高时需多取样。
2) 评估适应度
接下来,对获得的样本空间进行个体评价,步骤如下:
a) 考虑基因适应度的计算。在本接入环问题中,由于目标是令总花费最少,所以每个样本的路径总长越长,与目标越远,即两者负相关。因此,我们可以取函数1/S作为样本基因的适应度(S为样本的路径总长)。当然,还可以取其它类似的函数作为适应度,如当负相关程度较大时,可取1/S^2或者1/S^3等等,可按实际情况调整。
b) 评价每个基因,得到各自的适应度,并进行归一化,即使所有基因适应度相加为1,各基因按比例调整。
3) 繁殖
然后进行遗传算法中的关键操作,即对“基因库”进行选择、交叉、变异操作:
a) 选择。通过取随机数模拟基因被选中的概率,根据随机数落在样本适应度的空间位置判断,显然适应度大的“优秀”基因容易被选中,当然“不优秀”的基因也不会被完全放弃,这点十分重要。
b) 交叉。截取选中的基因的一部分,然后相互交换。在本接入环问题中,即按一定概率原则交换两个样本中不同路径中的一部分点的位置。优秀的基因可能在交叉中诞生。
c) 进行完交叉操作后需要重新约束每个样本,使其满足问题条件。
d) 遗传。对于一些相比之下“不优秀”的基因,我们单独随机修改其中的数据,即路径分配以及点的经过顺序。此项改动可以较大,以达到“基因突变”的效果,使其有可能成为“优秀”的基因。
e) 记录a)- d)的数据,得到新一代的“基因库”。
4) 下一代
最后,通过循环重复上述过程,使“基因库”不断更新并且遗传,记录每一代的最优解信息。迭代终止的条件为以下两种:
a) 认为设置迭代次数,如可设置到达1000次时迭代终止,最后的解即视为最优解。迭代次数的设置可视实际情况决定。
b) 观察每一代的最优解,当在很长一段时间内解不再更新,即可认为趋于稳定,此时可输出最优解。
3 数学建模
已知有起点(汇聚点A)与终点(汇聚点B)两个点,此外还分布着N个点(宏基站),各点两两之间可能连通(有直达接入层光缆),亦可能不连通(无直达接入层光缆)。要求由起点开始经过某些点到达终点,所经过的点有数量限制(环路最小节点数设为MIN,环路最大节点数设为MAX),路径数无限制,但最终且必须遍历每个点。通过结合遗传算法最终求出最优拓扑结构及建网总花费[8,9]。
限定条件为:单个环网最大节点数小于8个且不能产生同缆环即同一环路拓扑中相同路径不得经过2次。
已知条件为:管线费用成本(通过站点管线长度矩阵表确定)、设备费用成本(汇聚端口占用+基站接入设备)。
设由起点出发分出K条路径,K的值由算法动态决定。每条路径的初始载重为1,随着深度搜索载重变为hk(k=1,2,3……N),每个点的权重di为(i=1,2,3……N),N为离散点的个数。离散点i到离散点j之间的相关度为Cij。所有点的总集合设为{Q}。
设nk为第k条路径需要经过的离散点总数,用集合Rk{rki≤i≤nk}来对应第k条路径要经过的离散点,其中rki表示第k条路径要到达的第i个离散点。
rk0为第k条路径的起始点。
目标函数:
使得满足如下条件:

.
(1)
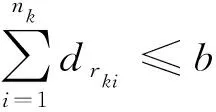
(2)
MIN≤nk≤MAX(k=1,2,…,K).
(3)
Tkx(rkm,rkl)≠Tky(rkl,kkm),
Tkx,Tky∈Tk,x,y=1,2…,nk+1^x≠y.
(4)
上述表达式中:式(1)表示所有离散点都应遍历,但可重复使用;不等式(2)表示每条路径的权重不超过路径的载重;不等式(3)表示每条路径经过的离散点总和不大于最大要求点数,且不小于最小要求点数;式(4)表示每条路径不走回头路,也不两次经过相同的线段,即避免成同缆环。
4 实例验证
以某运营商片区现有站点分布为例,我们对此片区的拓扑进行优化。

图3 某运营商片区站点分布
如图3所示,该区域现有2个汇聚节点:分别定义为(O)和(Z),周边分布有10个现有机房,分别编号为基站(A)……(Y)。将现有的光缆长度按照0.12元/纤芯公里进行折算,得到各站点之间管线连接成本矩阵表。其中,99表示无现有直达光缆,需要新建(实际运用中可考虑新建成本,按照1.5万元/公里*光缆长度+需要新建管道长度进行折算,本例中为演示方便,统一按99考虑)。
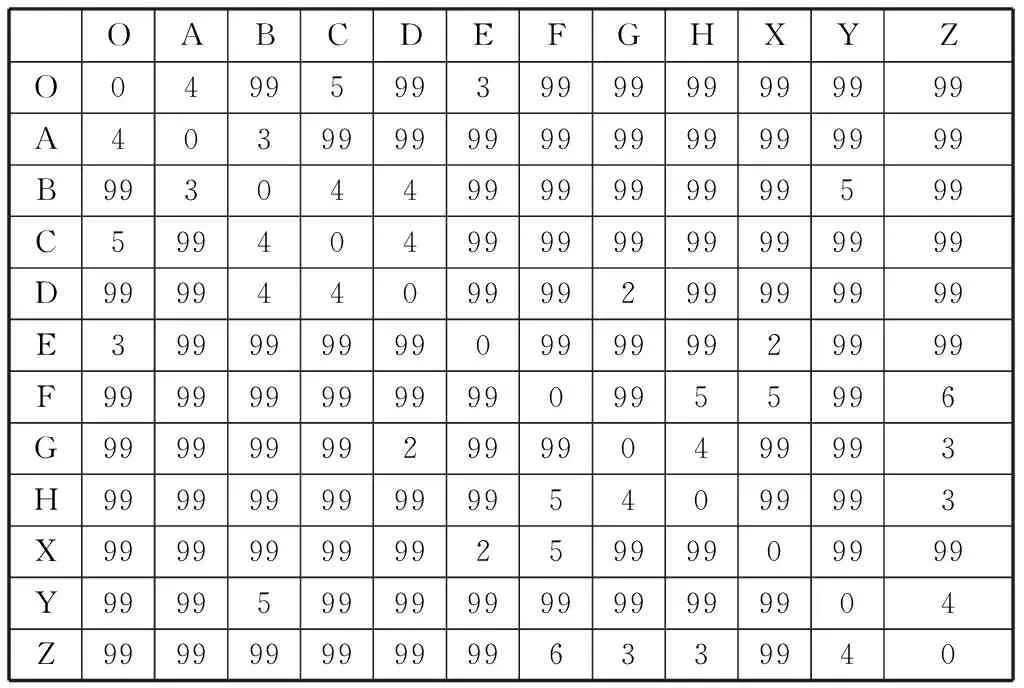
表1 站点连接成本路由矩阵表(单位:千元)
本次设定单个接入环的环路节点数量上限为4,下限为1,建立数学模型后,利用遗传算法求解。我们采用matlab进行编程运算,设定100次迭代计算之后,返回结果如图4所示。
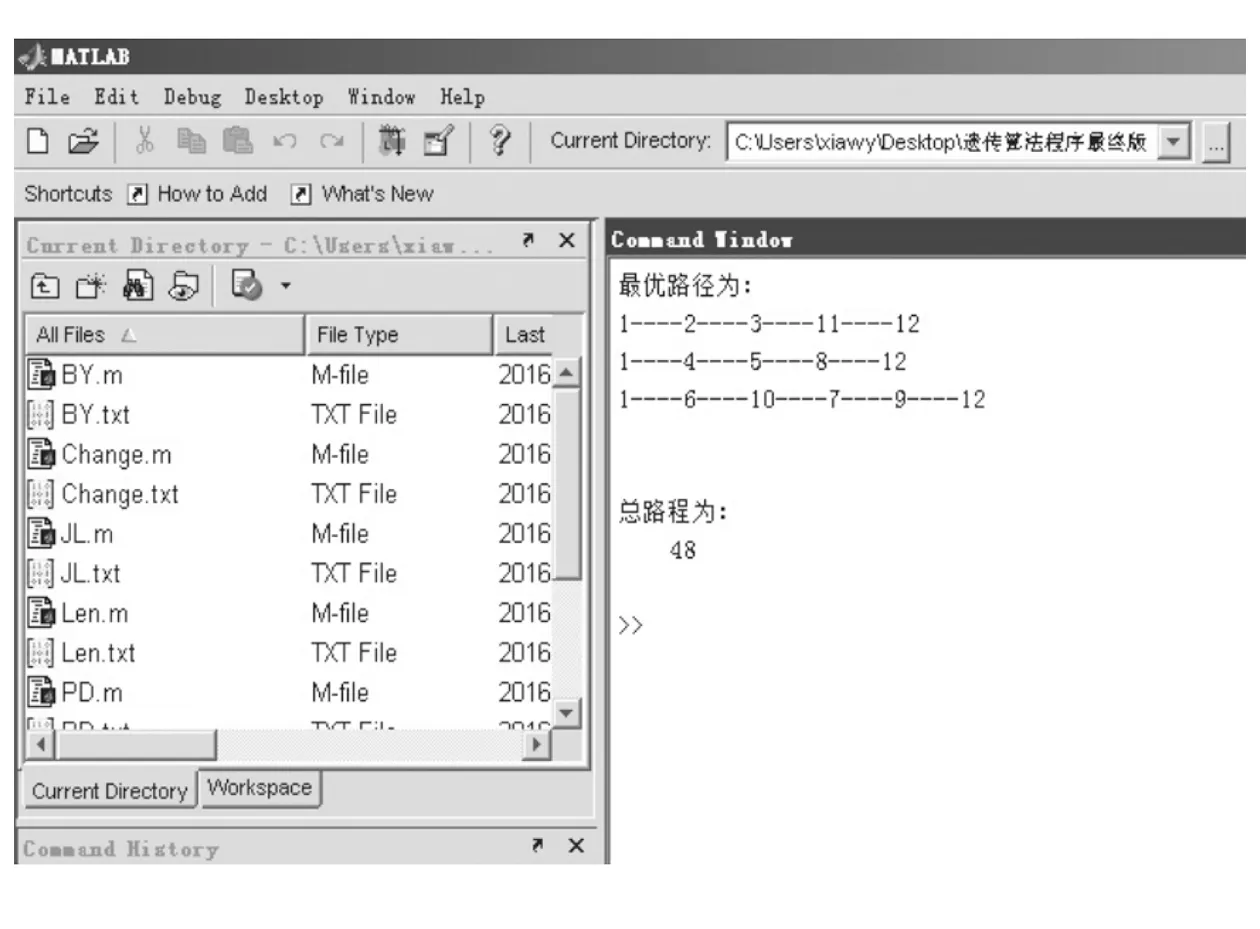
图4 程序计算结果
程序中总路程48表示总的费用成本花费4.8万元,数字和基站点位对应情况如下:

程序值123456789101112基站编号OABCDEFGHXYZ
即程序输出的最优拓扑环路数量为3,拓扑路径如下:
1) O-A-B-Y-Z
2) O-C-D-G-Z
3) O-E-X-F-H-Z
最优路线图输出如图5所示。

图5 拓扑最优路线路
5 结束语
本文借助数学模型的思想,将电信通信网络传输系统的拓扑优化抽象为NP-Hard问题,并利用遗传算法,使得在满足网络覆盖和安全的前提下,整体建网成本最低。这为运营商实现低成本、高效率地进行传输拓扑优化提供了一个合理的解决方案,在实际开发和应用中具有很高的借鉴和参考意义。
