拉格朗日松弛法在机组组合中的应用
2018-11-09杨立
杨 立
(山西大众电子信息产业集团有限公司,山西 太原 030024)
1 机组组合问题的提出
机组组合问题,是在电力系统中根据负荷预测各发电机组的成本,决策各机组在未来调度周期内各个时段的开停机计划,在满足系统负荷需求和各类约束条件下,实现总成本最小。电力系统的负荷是变动的,白天以及晚上刚开始的时候负荷是比较高的,而在凌晨时负荷是处于低谷的;工作日的负荷就要比周末的负荷要高。电力是不能被大规模存储的,发电量和用电量要处于平衡的状态,因此不同时间段内要进行不同的机组组合以满足这种平衡的需要。
开启足够的机组以满足系统最大的负荷,会造成相当大的浪费,在某些时刻关掉一些机组,会节省很大费用,从经济性上考虑,机组组合是非常有必要的。另一方面,机组有最小出力限制,在负荷低谷的时候,这么多机组同时运行,可能不能满足负荷平衡的要求。因此,恰当的机组组合对电力系统的安全经济运行是非常重要的。
2 机组组合问题的数学描述
2.1 机组组合的目标函数

(1)
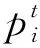
2.2 机组组合的约束条件
功率平衡约束:
(2)
机组启停次数约束:
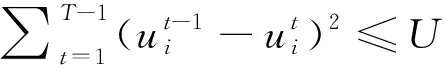
(3)
最小运行时间约束:
(4)
其他约束:如水火协调、必须运行机组、燃料限制、环境约束、电网安全。
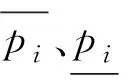
3 机组组合问题的求解
从数学角度看以上目标函数以及约束,机组组合问题具有高维数、非凸、离散、非线性的特点,在数学上为NP-Hard问题。现阶段应用于电力系统机组组合问题的算法大致分为两类:一类是传统算法;另一类是基于人工智能的算法。本文主要对传统算法中的拉格朗日松弛法在机组组合中的应用进行研究。
3.1 拉格朗日松弛法基本思路
拉格朗日松弛法在机组组合中的应用是通过求解对偶问题来得到原问题的解的,它通过一种松弛技术,避免了因耦合带来的“组合爆炸”问题,具体推导如下[1]:
在目标函数中针对系统耦合约束(负荷平衡约束和备用约束)分别引入拉格朗日乘子λ和μ,得到增广函数:
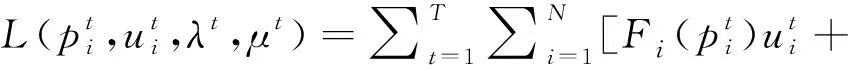
(5)
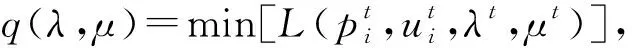
其对偶问题为:
(6)
对偶问题是一个极大极小问题,意义是对于不同的λ和μ,增广函数有不同的最小值,这些最小值中最大者为最优解。如果原问题符合凸规划条件,则满足强对偶定理,即对偶问题的最优解就是原问题的最优解。但机组组合问题的决策量为0-1变量,是离散、非凸的,不满足对偶定理,因此对偶问题的最优解同原问题最优解之间必然存在对偶间隙[2]。
将得到的增广函数变换形式:
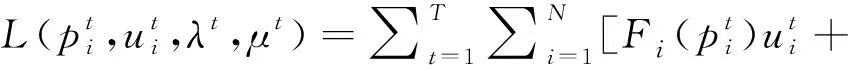
(7)

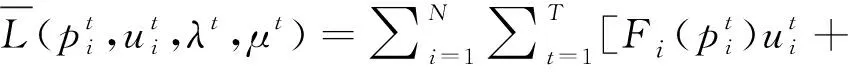
(8)
这样就能实现机组之间的解耦,也就是说
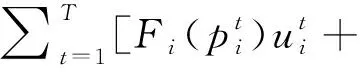
(9)
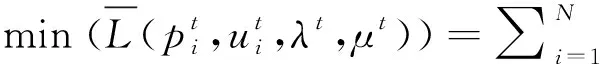
(10)
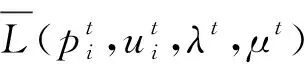
(11)
求解的结果是:
(12)
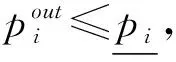
3.2 拉格朗日乘子初值选择以及调整
首先求q(λ,μ)对λ和μ的梯度:
(13)
(14)
(1) 对λt的调整[3]
当备用约束不满足时,
(15)
λt,k+1=βλt,k+(1-β)bt,k
(16)
其中β在0.4到0.8之间。
(2) 对μt的调整[3]
直接用梯度进行调节往往比较慢,通常采用如下方式进行调至。
第一次迭代时令εt,0=0。第k次迭代时,有εt,k。

μt,k+1=μt,k,εt,k+1=εt,k
(17)
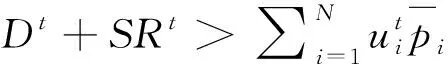
(18)
其中ε取所组合机组中容量最小的上限值。
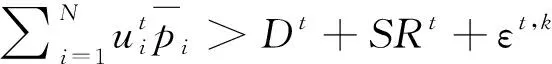
(19)
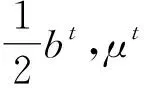
3.3 拉格朗日松弛法计算
拉格朗日松弛法最大的优点在于它的计算量与系统规模成线性关系,克服了维数障碍,机组越多算法效果越好,因此适用于大规模的系统优化问题。其缺点在于:当目标函数非凸时,利用对偶方法求解,存在对偶间隙,需要根据对偶问题的优化解不断更新拉格朗日乘子最终得到更精确的最优解,这是拉格朗日松弛法的一个难点。另外,在算法的迭代过程中可能出现振荡或奇异现象,需要采取适当的措施加快收敛速度[4]。
4 算例分析
4.1 算例
该算例是拿文献[1]中TABLE 5.4中的例子作为算例的。
在此算例中,成本函数为机组出力的一次函数,亦即:
F(P)=无负载时成本+成本微增率×P
(20)
由于成本函数为线性函数,在进行经济调度时,各机组按比费用由低到高的顺序依次从下限功率调至上限功率,从而完成最优经济调度。
由于启动方式有冷启动和热启动两种方式,冷启动方式在平时停机过程中是不耗能的,而热启动方式在平时停机过程中是要耗能的,本文在处理的时候将每个机组的状态稍微做了修改,传统的状态一般为0-1两个状态,本文在设置时设置了{00(停机状态且启动为冷启动方式)-01(停机状态且启动为热启动方式)-10(开机状态)}这三个状态,以便能够将启动的两种方式也都能考虑进去。这样四台机组连接起来就是一个八位二进制数,在本文中将其转换为了十进制,比如00101001,表示第一台机组关机,且开机方式为冷启动方式,第二台机组开机,第三台机组开机,第四台机组关机,开机方式为热启动方式,十进制数为41。
4.2 拉格朗日松弛法计算结果
经过了14次迭代,对偶间隙终于收敛到了0.05内,最优机组组合见表1,拉格朗日乘子以及对偶间隙在迭代过程中的数值见表2。
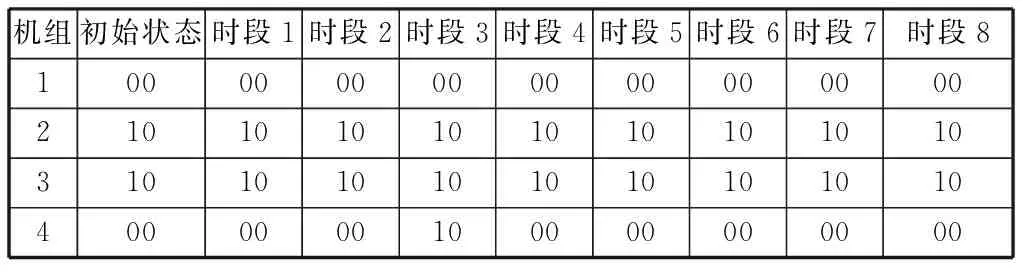
表1 最优机组组合
最小费用为7.410 99×104R。
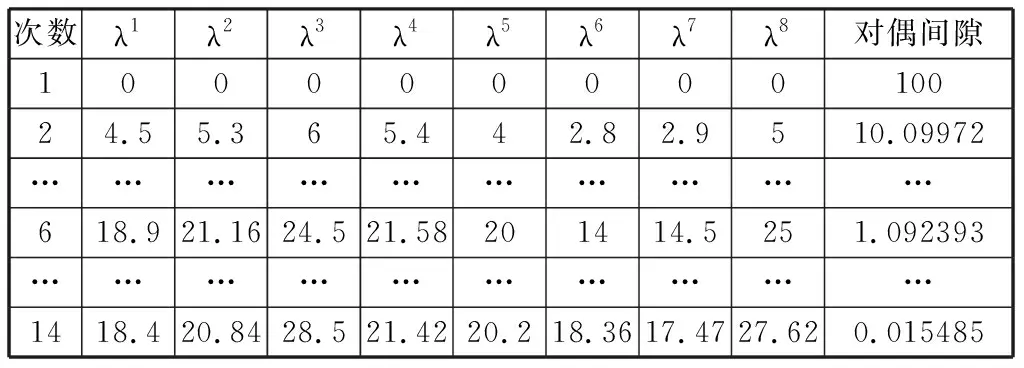
表2 拉格朗日松弛法迭代过程
5 结论
以上算例最终计算结果与原文一致,表明复现成功了。通过本次对机组组合问题的研究学习,基本掌握了解决机组组合问题的一种经典方法,可为日后的学习研究做基础。
