基于位姿反馈的三臂空间机器人抓捕轨迹规划

蓝启杰 刘宜成 张 涛

1.四川大学电气信息学院，成都，610065

2.清华大学自动化系，北京，100084

3.西昌卫星发射中心，西昌，615000

0 引言

空间机器人是代替或协助人类在太空环境中执行在轨服务的特种机器人，在降低成本和风险方面有突出的优势，已成为空间技术发展与应用的热点，其应用领域非常广泛，包括在轨组装、维护、清理、实验、辅助航天员活动等，由于其存在特殊的运动学和动力学性质，因此受到许多研究人员的关注［1⁃4］。

相比单臂和双臂空间机器人系统，三臂或多臂空间机器人更灵活，具备执行更加复杂任务的能力［5］。三臂空间机器人执行在轨任务时，可以采用多种工作方式。采用双臂抓捕操作、单臂稳定基座位姿的方案时，2个机械臂完成协同抓捕的任务，1个机械臂实现基座位姿稳定［6］。基于运动学特征方程求解关节运动轨迹是机器人连续路径规划的基本方法，但运动学或动力学奇异是机械臂的固有特性，在奇异点附近，采用雅可比矩阵直接求逆会造成关节角速度突变而导致控制不可实现。目前，已有学者提出回避奇异的方法来保证奇异点附近关节角速度的连续性和有限性，比如阻尼最小方差法［7］、选择性最小阻尼方差法［8］、“奇异分离+阻尼倒数”方法［9］、“奇异转化+阻尼倒数”方法［10⁃11］，这些方法都是在奇点附近对设计路径做微小改变，但都在不同程度上牺牲了位姿跟踪精度，即使机器人离开奇异区域，误差仍然存在。

为减小和消除上述方法的跟踪误差，本文在三臂空间机器人的轨迹规划过程中，引入机械臂末端和基座的位姿反馈，将机械臂关节角速度作为控制变量，设计闭环系统的反馈控制率，在误差运动方程上对关节角速度进行求解，实现高精度的位姿误差控制和轨迹跟踪。

1 三臂空间机器人模型

如图1所示，空间机器人系统由基座和在其上安装的3个机械臂组成，每个机械臂有6个自由度。机械臂1和机械臂2实现目标跟踪、抓捕，以下称为任务臂；机械臂3实现跟踪阶段和抓捕时刻的基座位姿平衡，以下称为平衡臂。图1中，j（j=1，2，3）为机械臂标识；i（i=1，2，…，6）为连杆和关节标识；ΣI为惯性坐标系；ΣE为末端坐标系；ΣB为基座参考坐标系；B0、C0分别为基座及其质心；Jj，i为机械臂 j连杆 i的关节；Cj，i为机械臂 j连杆 i的质心；aj，i、bj，i分别为机械臂 j的关节 Jj，i到质心 Cj，i的位置 矢 量 和 质心 Cj，i到关节 Jj，i+1的位置矢量；bj，0为基座质心C0到机械臂j的第一个关节 Jj，1的位置矢量；φk为矢量 bj，0与基座坐标系X轴的夹角。

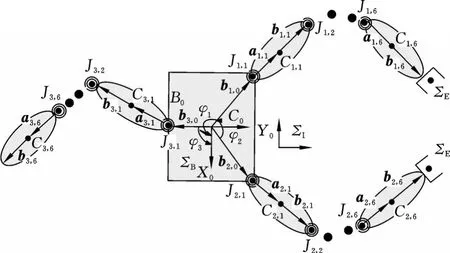
图1 三臂空间机器人结构模型Fig.1 Structural model of three-arm space robot

1.1 运动学模型

根据各连杆相对位置关系，可得各机械臂末端的位置矢量：

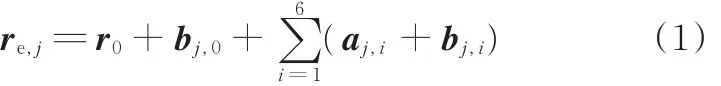
式中，re，j为惯性系下机械臂j的末端位置矢量；r0为惯性系下基座质心位置矢量。

根据各连杆相对速度关系，可得各机械臂末端速度矢量：

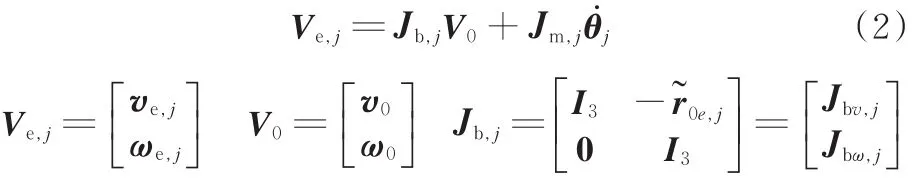
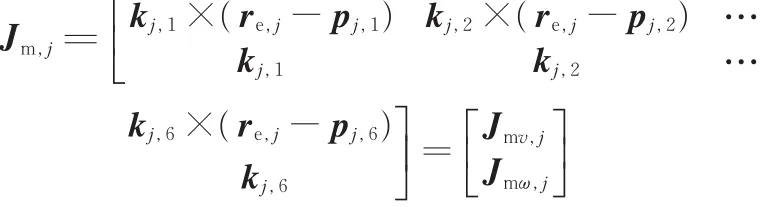
式中，Ve,j为机械臂j末端线速度ve,j和角速度ωe,j组成的矢量；V0为基座质心线速度v0和角速度ω0组成的矢量；Jb,j为基座雅可比矩阵；Jm,j为机械臂j雅可比矩阵；j为机械臂j的类节角速度。

整个系统的线动量

式中，Μ为系统总质量；JTω,j为系数矩阵；rog为系统质心相对于基座质心的位移矢量；C1为常数。

整个系统相对于卫星本体质心的角动量

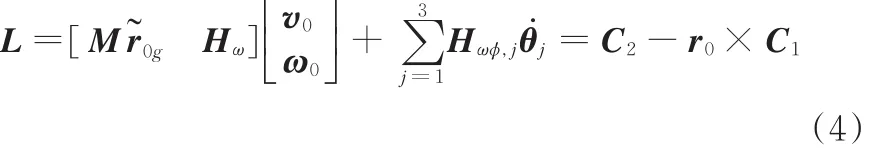
式中，Hω、Hωϕ为耦合矩阵；C2为系统相对惯性系的总角动量，为常数。

联立式（3）、式（4），可推导出基座质心速度矢量：

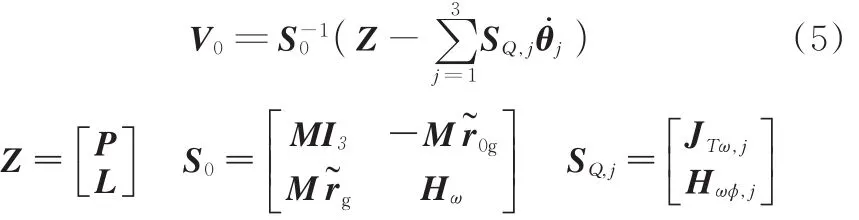
式中，~rg为整个系统质心的位置矢量。

1.2 误差运动学模型

在运动学模型基础上，引入期望位姿指令，可以得到系统的误差运动学模型。机械臂末端或基座质心位置误差及其导数可表示为

式中，p为末端或基座的实际位置；pd为末端或基座的期望位置；v为末端或基座的实际线速度；vd为末端或基座的期望线速度。

机械臂末端或者基座质心姿态误差可表示为

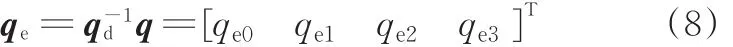
其中，qe为姿态误差；qd为期望姿态；q为实际姿态，均采用四元数法表示。姿态误差及其导数也可用修正的罗德里格参数表示为

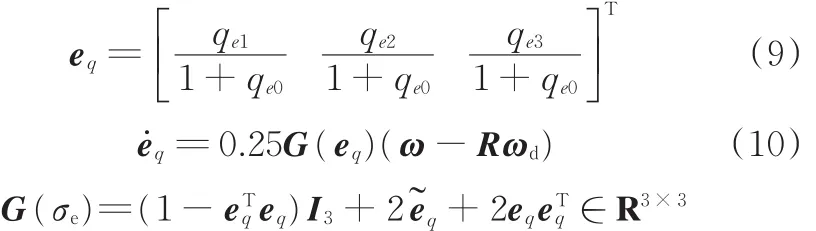
式中，eq为姿态误差；ω为实际角速度；ωd为期望角速度；R为实际姿态相对于期望姿态的旋转矩阵。

定义位姿误差矢量e=（ep，eq）T，综合式（7）、式（10）可得误差运动学方程：

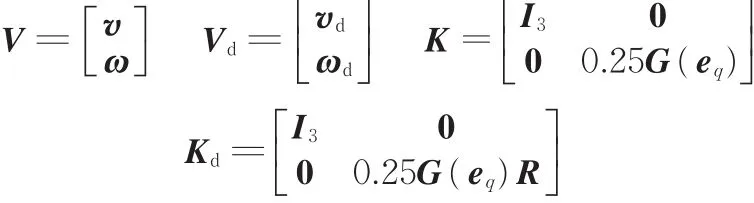
结合式（2）和式（11）可得2个任务臂末端位姿误差运动方程：

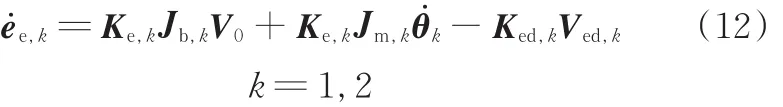
式中，k为关节角速度。

同理，可得基座质心位姿误差运动方程：

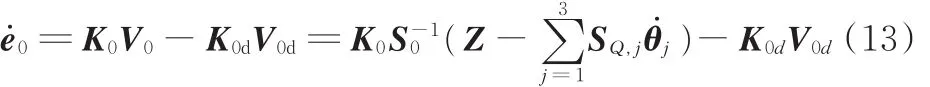
2 机械臂轨迹规划

空间机器人轨迹规划一般指在运动学或动力学的基础上，分析关节空间或笛卡儿空间轨迹的规划和生成。给定任务臂末端初始和目标位姿，可求出末端期望轨迹，然后通过运动方程反解即可得到任务臂关节角运动规律，当雅可比矩阵奇异时，需要采用避奇异算法。利用动量守恒方程对平衡臂进行速度级规划时也可能出现雅可比矩阵奇异的情况。如前所述，采用现有避奇异算法会产生末端或基座位姿跟踪误差。因此，本文根据误差运动学方程（式（12）、式（13））分别对任务臂和平衡臂进行轨迹规划。首先将2个任务臂关节的角速度作为控制变量，设计利用末端位姿反馈的控制器，实现末端高精度位姿跟踪。将任务臂规划得到的关节角速度视为常数向量代入式（13），将平衡臂关节角速度作为控制变量，设计利用基座位姿反馈的控制器，实现基座高精度的稳定。

2.1 任务臂轨迹规划

由式（12）看出，任务臂末端位姿误差运动状态可以通过任务臂关节角速度来控制，由此引入末端位姿误差，使得末端位姿运动满足：

其中，λe，k为末端位姿反馈增益矩阵，其对角元素都大于零。t→∞时，末端位姿误差ee，k将按指数速度渐进收敛至0，能实现对期望末端位姿的无误差跟踪。联立式（12）、式（14）可以求出任务臂关节角速度：

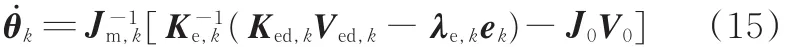
本文采用基座稳定无扰动的方案，即满足V0=06×1。当 Jm，k不可逆时，可采用“奇异分离+阻尼倒数”［9］或者DLS方法［12］求其近似值：

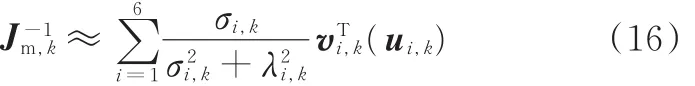
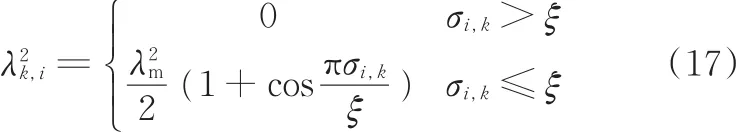
式中，λm为最大阻尼值；ξ为阈值；vi,k、ui,k为矩阵Jm,k的正交奇异向量。

引入阻尼系数后，机械臂关节角速度可以连续平滑地渡过奇异区域。

由于末端位姿反馈的引入，按照式（15）规划的任务臂关节角速度不仅可以实现末端位姿误差收敛至0，还可以减小奇异区域内的末端位姿误差，收敛速度通过设计反馈增益矩阵λe，k元素值进行调节。

2.2 平衡臂轨迹规划

任务臂规划完成后，将求得的关节角速度视为常量并代入基座质心位姿误差运动方程（式（13）），采用速度级方式对平衡臂关节角速度进行规划。六自由度平衡臂能同时抵消2个任务臂运动对基座质心位姿的耦合影响，达到稳定基座质心位姿的目的。由式（13）可以看出，基座位姿误差运动可以通过平衡臂关节角速度控制，由此引入基座位姿误差，使基座位姿运动满足：

与任务臂相同，λ0为对角元素都大于零的反馈增益矩阵，能使基座质心位姿误差收敛至0，达到稳定基座质心位姿的目的。

联立式（13）、式（18）可以得出平衡臂关节角速度：

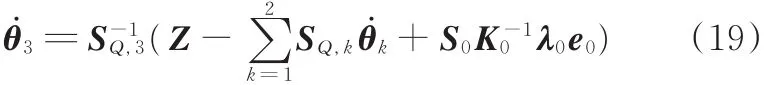
当SQ，3不可逆时，采用与任务臂相同的避奇异算法进行奇异回避。

由于基座位姿反馈的引入，按照式（19）规划的平衡臂关节角速度可以使基座位姿误差收敛至0，减小平衡臂奇异区域内基座位姿误差，还可以削弱外界扰动对基座位姿的影响，收敛速度通过设计反馈增益矩阵λ0元素值进行调节。

3 仿真分析

在建立三臂空间机器人仿真模型的基础上，对本文提出的轨迹规划算法进行了数值仿真，并且同“奇异分离+阻尼倒数”的轨迹规划方法［7］进行了对比分析。

3.1 仿真模型

仿真实验的3个机械臂均采用PUMA560型，且均采用D⁃H参数建模［13］，机械臂D⁃H坐标系结构如图2所示，D⁃H参数值如表1所示。基座、机械臂质量特性参数如表2所示。

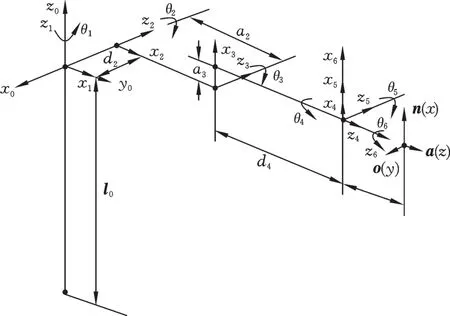
图2 机械臂D-H坐标系Fig.2 D-H coordinate system of manipulator

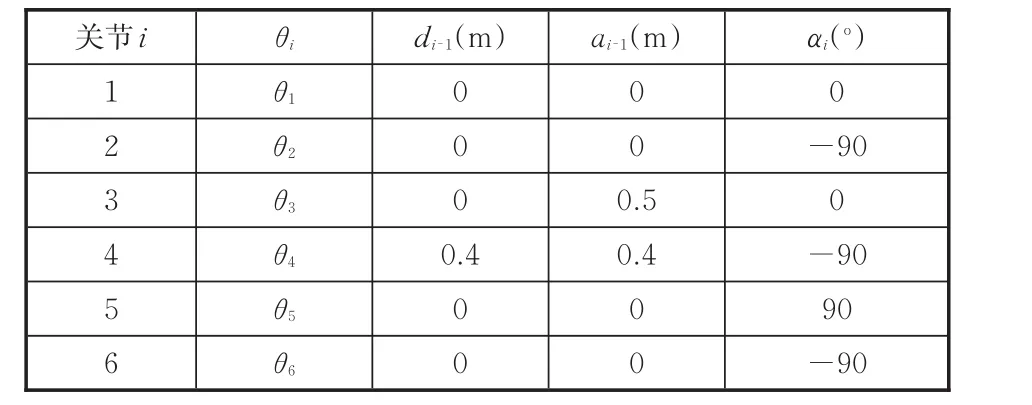
表1 D-H参数Tab.1 D-H parameters

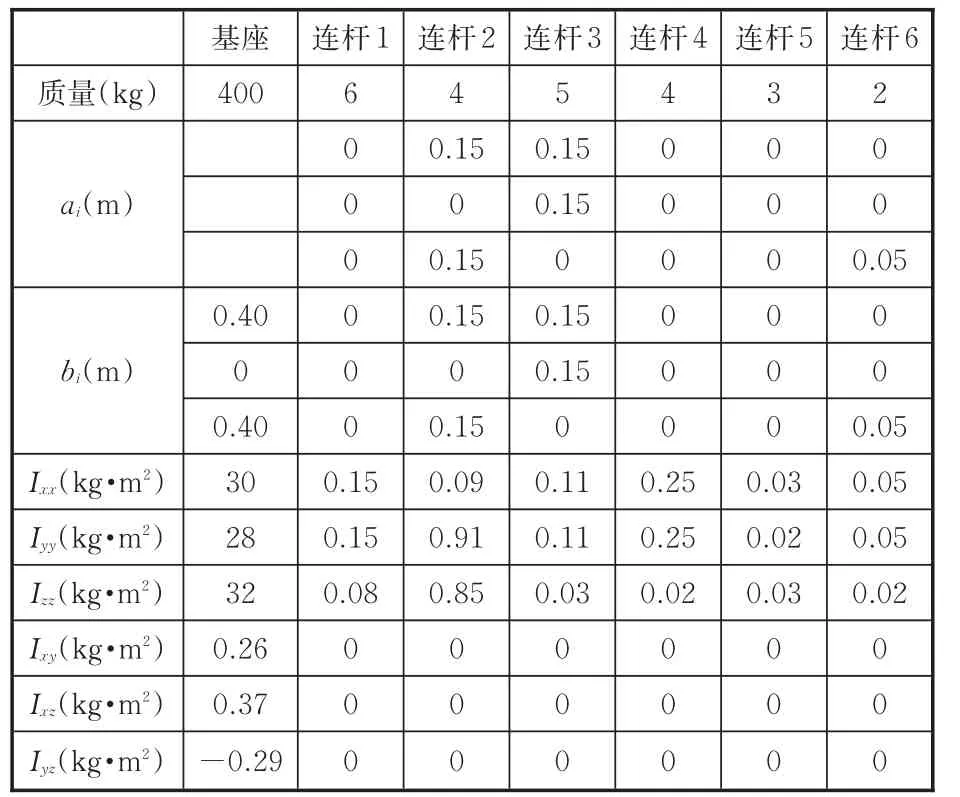
表2 空间机器人质量参数Tab.2 Mass properties of space robot

3.2 轨迹规划仿真

利用MATLAB/Simulink工具对运动学模型和规划算法进行验证。假设系统初始线动量和角动量均为0，仿真时间tf=20 s。最大阻尼值λm=0.05，奇异阈值ξ=0.10，反馈增益矩阵为diag（2，2，2，2，2，2）。

任务臂1末端惯性系下初始位姿为

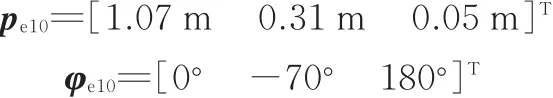
任务臂2末端惯性系下初始位姿为

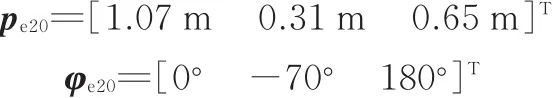
两个任务臂末端惯性系下目标位姿为

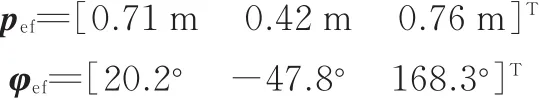
基座惯性系下的初始位姿为

任务臂初始关节角为

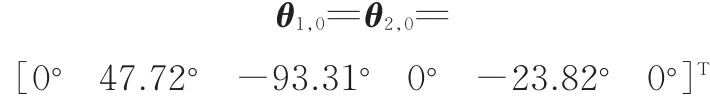
平衡臂初始关节角为

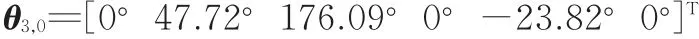
任务臂与平衡臂的关节角速度如图3～图5所示。

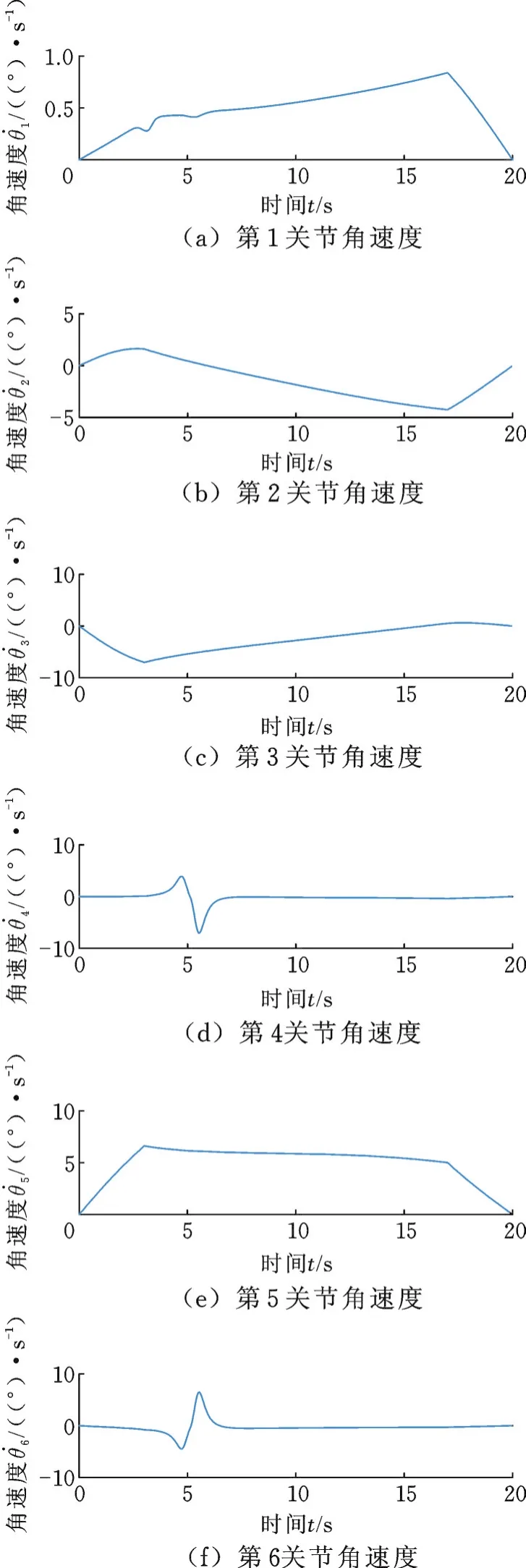
图3 任务臂1关节角速度Fig.3 Joint angular velocity of the first task arm

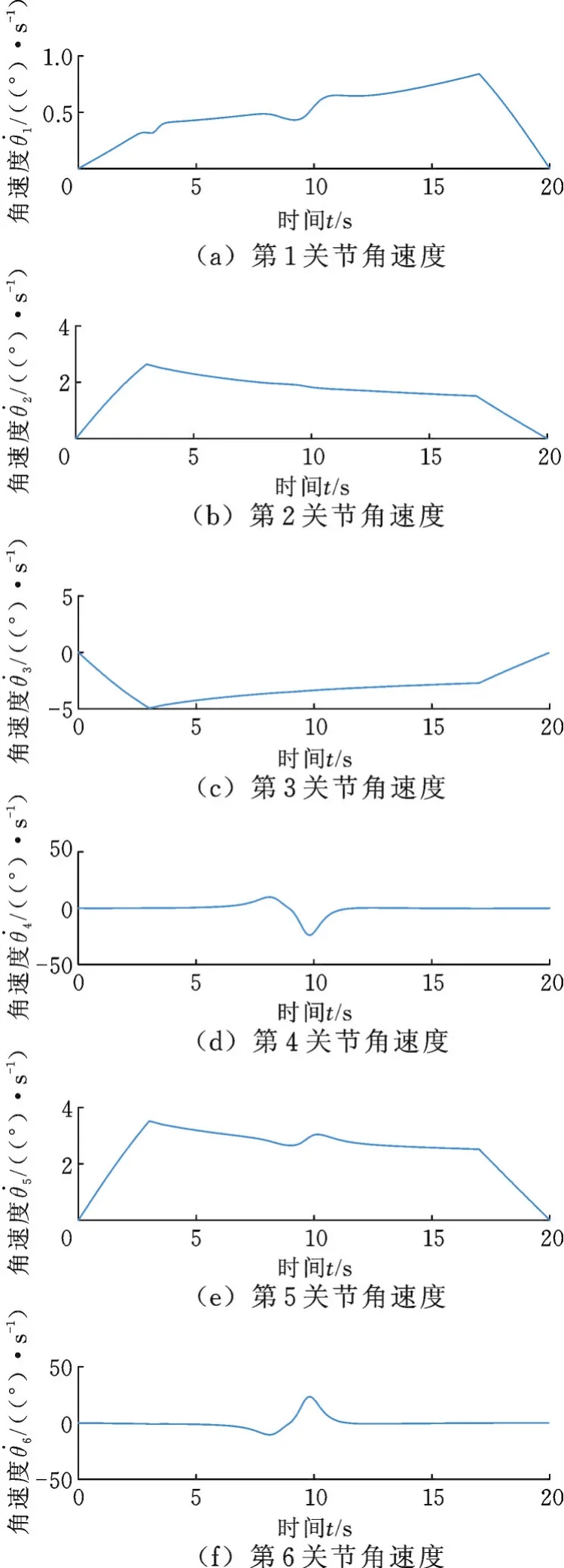
图4 任务臂2关节角速度Fig.4 The joint angular velocity of the second task arm

由图3～图5可以看出，机械臂关节角速度变化趋势连续平稳，系统模型准确，算法有效。机械臂最大关节角速度为18°/s，满足机械臂运动限制要求。

由图6、图7可看出，任务臂1在5.1 s时产生腕部奇异，任务臂2在8.9 s时产生腕部奇异，平衡臂在3.1 s时产生腕部奇异。由于阻尼系数的引入，任务臂1末端在4.1 s时开始出现位姿跟踪误差，位置跟踪最大误差（三轴合成）为2.1×10-4m，末端姿态跟踪最大误差（轴角法）为0.2°。任务臂2末端在7.1 s时开始出现位姿跟踪误差，位置跟踪最大误差（三轴合成）为6.3×10-4m，末端姿态跟踪最大误差（轴角法）为1.1°。任务臂渡过奇异区域后，末端位姿误差收敛至0。基座在1.7 s时开始出现位姿误差，位置跟踪最大误差（三轴合成）为2.6×10-5m，姿态跟踪最大误差（轴角法）为0.05°。平衡臂渡过奇异区域后，基座位姿误差均收敛至0。

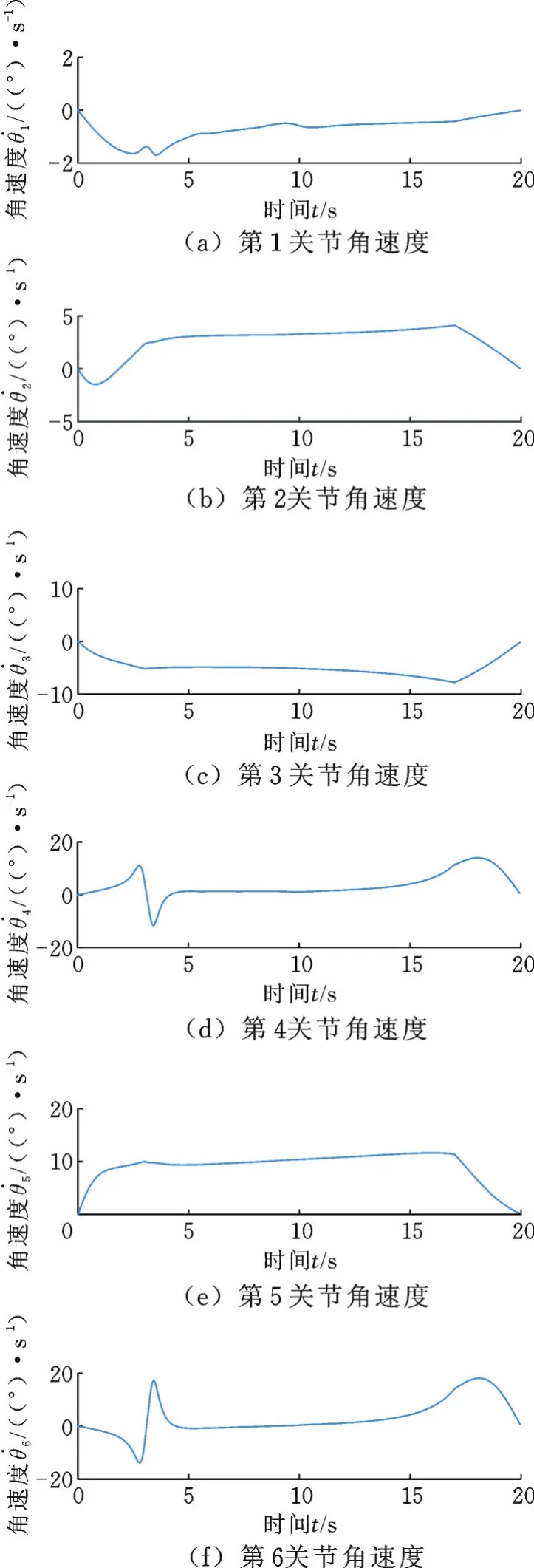
图5 平衡臂关节角速度Fig.5 The joint angular velocity of the balance arm

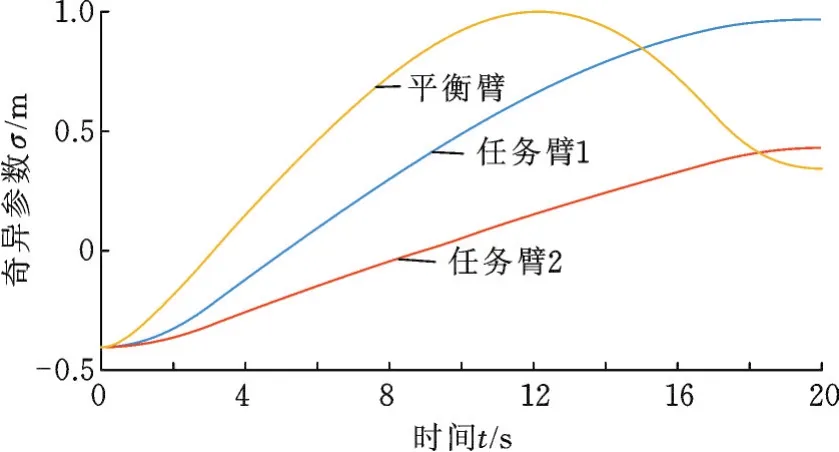
图6 腕部奇异参数Fig.6 Singular parameter of wrist

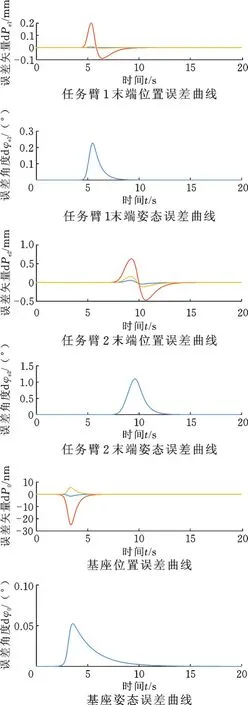
图7 任务臂末端位姿误差和基座位姿误差Fig.7 The pose error of end-effector and base

由图8看出，仅采用“奇异分离+阻尼倒数”回避奇异时，任务臂1末端位置跟踪最大误差为0.5×10-3m，姿态最大误差为0.3°。任务臂2末端位置跟踪最大误差为2.9×10-3m，姿态最大误差为1.6°。基座位置跟踪最大误差为3.9×10-5m，姿态最大误差为0.05°。机械臂末端和基座位姿误差在机械臂产生奇异后一直存在。引入位姿反馈控制后，奇异区域内位姿跟踪误差减小，机械臂渡过奇异域后误差均收敛至0。

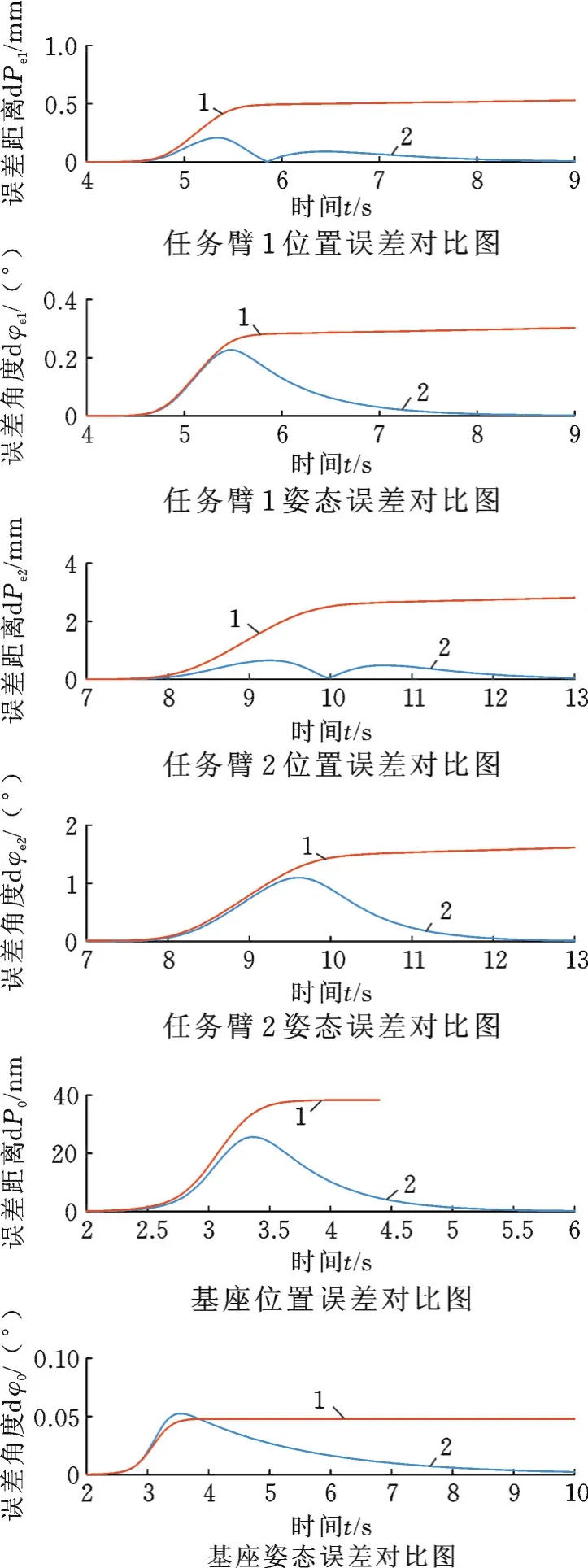
图8 两种方法的误差对比Fig.8 Error comparison of two methods

综合上述仿真结果可以看出，本文方法不仅能减小机械臂在奇异区域内出现的位姿跟踪误差，而且在机械臂渡过奇异区域之后，该误差能快速收敛至0，完成末端高精度跟踪连续路径的任务，同时确保基座位姿无扰动。

4 结论

本文提出的“位姿误差反馈”方法不需要对机械臂构型进行详细的分析，对机械臂的质量也没有任何的特殊要求，具有很好的通用性，而且能同时应用在单臂、双臂等多种空间机器人系统构型上。理论和仿真结果表明，对于连续路径跟踪，以前的回避奇异方法并未对阻尼系数所引起的误差进行处理。本文方法将轨迹规划问题转化为控制问题，不仅可以减小由阻尼系数带来的位姿跟踪误差，而且在机械臂渡过奇异域之后还可以彻底消除末端或基座的位姿跟踪误差。