金属波纹管单点增量成形过程研究

石 珣 李 言 杨明顺 姚梓萌 侯晓莉

西安理工大学机械与精密仪器工程学院，西安，710048

0 引言

金属波纹管是一种外型呈现规则波浪样、带有横向波纹的管状零件。它不仅具有高的弯曲疲劳强度和弹性稳定，而且在外力作用下能产生轴向、横向、角向位移，在国防、石油化工、航空航天等各种工业领域广泛应用［1］。传统的波纹管加工方法有焊接成形、机械成形和液压成形等，在工艺流程中的关键工序容易出现未焊透和气孔以及圆度低、波形不饱满等各类缺陷，难以保证最终成形件的质量［2］。

管类零件单点增量成形技术引入“分层制造”的思想，通过一个简单成形工具施加载荷，按照预先设定好的成形轨迹，逐次分层得到需要的零件，可以成形多种复杂成形零件，该工艺不需要预先制造模具、所需制造周期短，适应于多品种小批量生产和低成本快速成形新产品［3⁃4］。

目前，已有学者进行了将单点增量和薄壁管成形相结合的成形分支管的研究。TERAMAE等［5］进行了薄壁管增量成形分支管管壁材料变形行为的研究，结果表明各向异性（R值）不影响厚度减薄率，分支管厚度减薄分布几乎是均匀的。YANG等［6］基于实验进行了不锈钢薄壁管增量成形分支管的研究，得到不锈钢薄壁管增量成形分支管的推荐尺寸，同时对增量成形分支管实验中出现的缺陷原因进行了分析。管成形工艺研究方面，RAUJOL⁃VEILLÉ等［7］进行了薄壁钢管增量成形轴承内圈工艺的研究，发现优化的成形工艺可降低1/4回弹量。ALVES等［8］利用模具对薄壁管的一端进行成形研究，获得了薄壁管成形中延性破损等成形极限时的工艺参数。程秀全等［9］进行了非轴对称管件缩径成形的研究，分别得到了偏心类和倾斜类管件缩径成形的最优工艺参数组合。WEN等［10］提出了一种薄壁管增量成形工艺，并通过实验成形了一些传统工艺较难成形的特殊形状零件。

管成形技术研究其他方面，BECKER等［11］提出了一种管件弯曲增量成形工艺，与传统成形工艺相比，增量成形工艺应力叠加小，弯矩和回弹量也小。MOHEBBI等［12］进行了管件流动旋压成形，发现管旋压成形中的剪切应变不仅发生在纵向，也发生在横向，综合影响成形管件几何精度。KUWABARA［13］提出了一种高温条件下铸造铝合金管的流变成形工艺，并通过实验验证了仿真分析的准确性和鲁棒性。MOHEBBI等［14］进行了增量成形多层复合管研究，分析工艺参数对多层复合管成形粘结强度的影响。

由上述管类零件单点增量技术国内外研究现状的分析可知，目前的研究主要集中在成形工艺开发、工艺优化和材料变形行为方面，还没有学者进行单点增量成形技术与波纹管成形相结合的研究。笔者将单点增量技术引入波纹管成形工艺，利用有限元数值模拟，研究金属管单点增量成形过程，分析过程中成形力的变化趋势、材料变形位移和塑性应变分布的变化规律，并通过实验进行验证。

1 成形原理

金属管单点增量成形原理如图1所示。通过导轨控制刀架上的工具轮X向（管的径向）层进给后，沿着Y向（管的轴向）对管壁加工成形，最终经过多道次层进给完成成形过程。其中，vx、vy分别为工具轮X向（径向）进给速度和Y向（轴向）进给速度。图1中，n为机床的主轴转速，L为管料原始长度，l为波纹轴向长，t0为管料的原始壁厚，t1为成形工件圆弧顶点处的管壁厚度，b为工具轮的厚度，r为管料原始外半径，R为成形工件波峰处管外半径，z为工具轮两层成形轨迹的高度差，α为成形波纹斜壁角度。金属管单点增量成形装置如图2所示，夹紧装置分为管芯轴和三爪卡盘，将芯轴装入金属管中，防止三爪卡盘夹紧金属管导致的管壁变形。

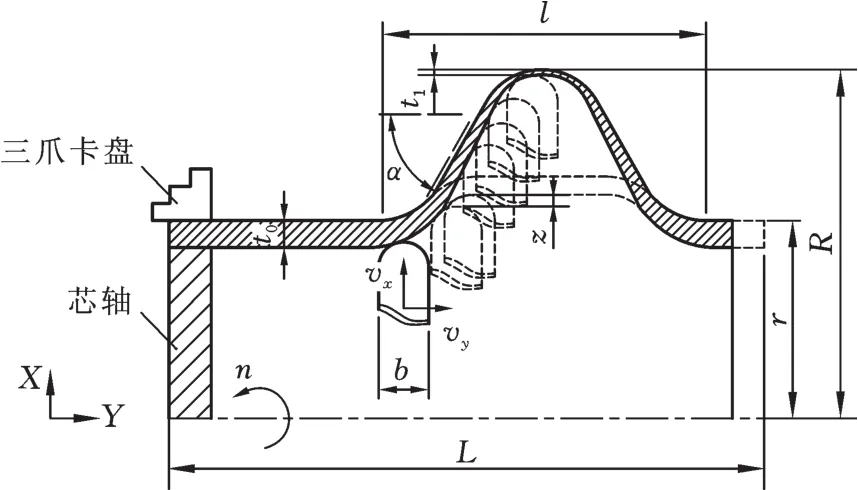
图1 金属管单点增量成形原理Fig.1 Incremental forming principle of metal tube

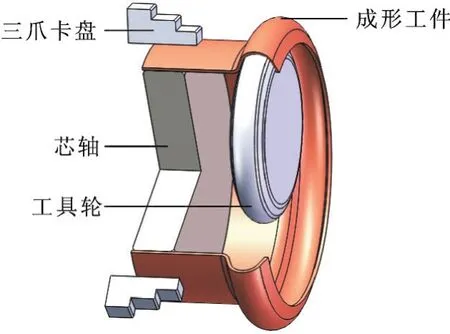
图2 金属管单点增量成形装置Fig.2 A clamping device of metal tubes

2 有限元模型的建立

金属管选用T3紫铜材料，其化学成分（质量分数）见表1，材料性能参数见表2，增量成形实验参数见表3。

表1 T3紫铜管的化学成分（质量分数）Tab.1 Chemical composition of T3 red copper（mass fraction） %

表2 T3紫铜材料性能Tab.2 Uniaxial tensile properties of T3 red copper

表3 T3紫铜管的增量成形实验件参数Tab.3 Incremental forming part of process parameters

金属管增量成形过程中，工具轮头部的圆弧半径为3 mm，工具轮的厚度b=8 mm，工具轮层进给成形路径如图1所示。通过拉伸实验得到该T3紫铜管塑性应力应变关系，如图3所示。

有限元模型中的金属管毛坯（T3紫铜管）选择各向同性本构模型；相互作用模块（工具轮和管壁之间）采用库仑摩擦条件，摩擦因数设定为0.1；接触选择面与面接触，接触算法选择罚函数算法；网格模块单元类型选择实体单元C3D8R，规格为0.5 mm×0.5 mm×0.5 mm；分析步模块采用动力、显式（Explicit）分析步。为了节省计算总时间，加快模型计算速度，质量放大系数设定为1 000，工具轮采用解析性旋转刚体模型。建立的金属管单点增量成形有限元模型如图4所示。

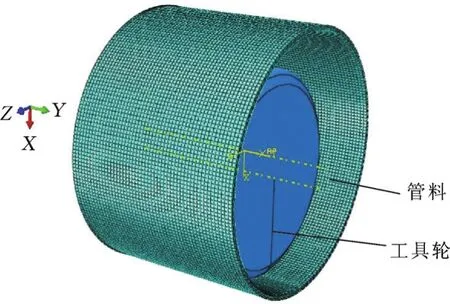
图4 金属管单点增量有限元模型Fig.4 Finite element tube model of SPIF

3 仿真结果分析

3.1 成形力

上述有限元模型总共经历12层成形路径，分析得到模拟成形结果，在一个分析步中提取20个点，得到X、Y、Z三个方向的分力随时间的变化，如图5所示。由图5可以看出，成形过程中，X向分力Fx、Y分力Fy和Z向分力Fz在成形最初阶段不断上升之后在稳定曲线的上下波动，X向分力相比Y、Z方向的分力大，X向分力在金属管单点增量成形过程中对成形性的影响较大。

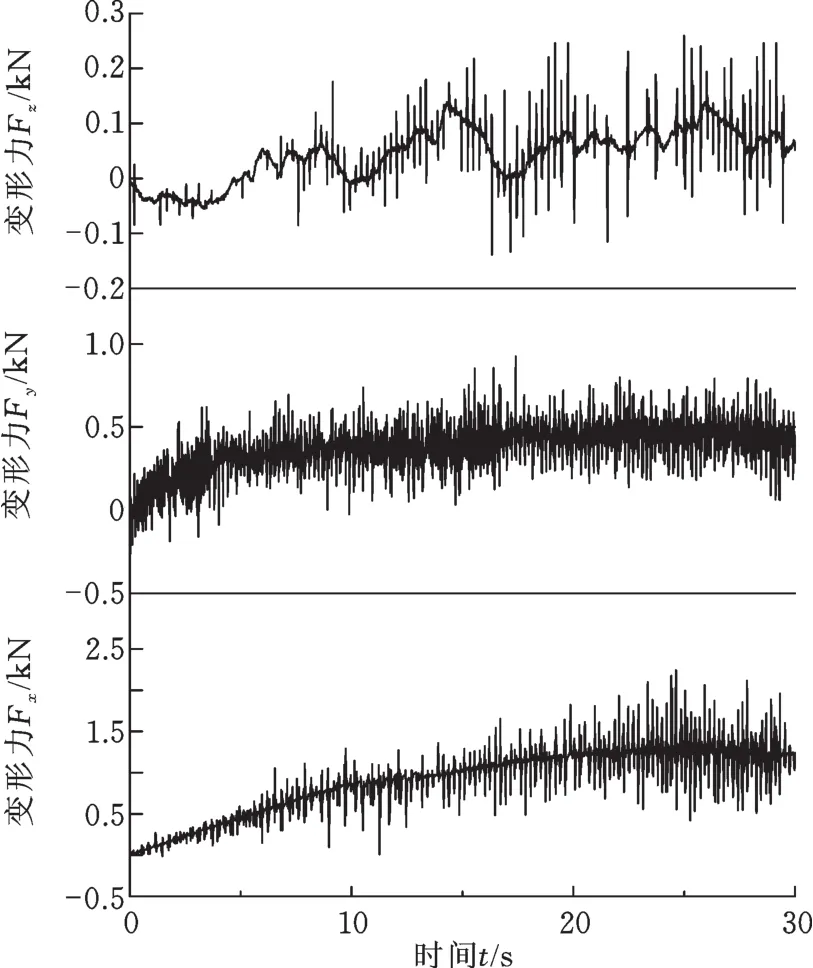
图5 有限元模型成形过程三向力Fig.5 Evolution of three orthogonal directions predicted by finite element simulation

3.2 成形应力

金属管增量成形过程中的等效应力分布变化如图6所示。在增量成形25%时，应力集中在工具轮和管壁接触区域；随着工具轮层进给成形，应力集中在管壁变形区的中部和变形区边缘处；成形完成后，管壁变形区边缘处有较大的应力集中，如图6d所示。

图6 成形过程应力分布Fig.6 Stress distribution during forming process

3.3 管壁材料局部变形位移

在成形区管壁内外两侧设置6个高斯点（图7），分析成形过程中工具轮X方向从0.5 mm位置成形移动到3.5 mm位置时这6个高斯点的位移，评判金属管增量成形过程中管壁材料局部变形位移是否对成形质量有影响。成形过程不同的2个成形瞬间中，工具轮分别进行了6次层进给，从X向的0.5 mm位置移动到3.5 mm位置。3个高斯点的位置在管壁的内表面，记为GPx_L；另外3个高斯点的位置在管壁的外表面，记为GPx_U。图7中两个相邻高斯点之间的初始距离是1 mm。

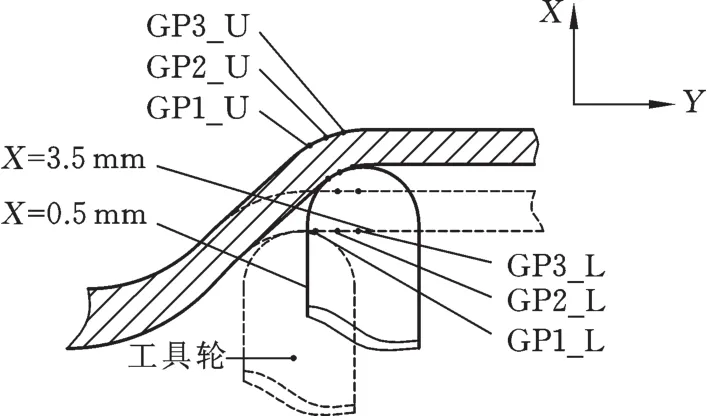
图7 管壁6个高斯点的位置Fig.7 Location of six Gauss points used to evaluate the local springback

增量成形过程中的管壁材料局部变形位移，可以通过分析工具轮加载在管壁X方向变形位移得出。选定的6个高斯点的X坐标随成形时间变化，如图8所示，截取的仿真成形分析步时间是17 s。工具轮在X正向对管壁进行成形，位于上表面的3个高斯点与下表面3个高斯点的X正方向位移是相似的。

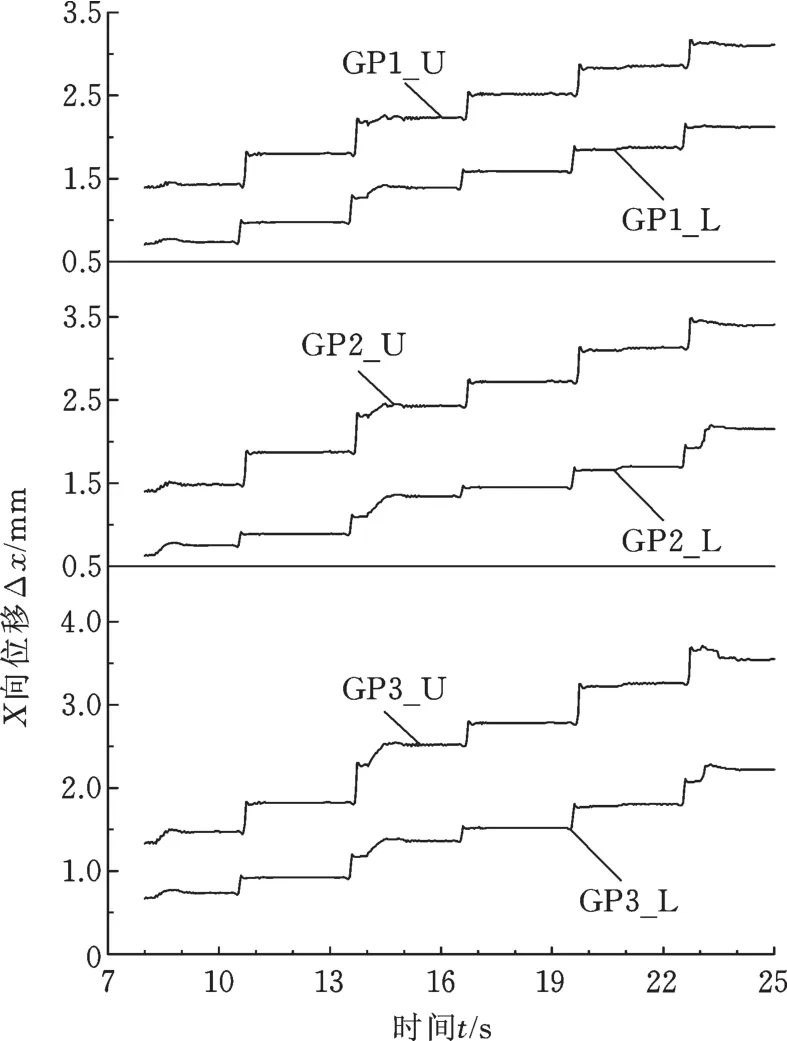
图8 6个高斯点X向位移数值变化Fig.8 Numerical evolution of the X-coordinate measured in six different Gauss points of the sheet

通过分析仿真增量成形过程中管壁上的高斯点X方向位移，可以间接预估局部成形区域的变形位移情况，如图8所示，管壁连续变形时的变形位移最为突出。当工具轮前端经过第一个高斯点GP1_L时，该点的高度高于GP2_L和GP3_L，即GP1_L的X向位移大于GP2_L和GP3_LX的X向位移；当工具轮前端离开高斯点GP1_L，层进给成形管壁时，GP1_L点X向位移变化量与GP2_L和GP3_L点位移变化量相比，呈现降低趋势。高斯点GP1_U开始成形到最终成形结束，从第13 s开始，GP1_U的X向位移值变化量与GP2_U和GP3_U的X向位移变化量相比，快速减小。最终时刻GP1_L点的X向位移和GP1_U高斯点趋势一致，X向位移分别小于内表面和外表面其他两点的位移。金属管装夹固定端距离成形区域管壁有一段距离，已成形管壁的局部区域缺少固定支撑是该区域发生负向运动趋势的主要原因。

3.4 成形应变

图9所示为仿真成形件最大塑性应变和最小塑性应变对比曲线。距起点12.42 mm位置（厚度减薄最大位置）的塑性应变最大；管口方向距起点5～10 mm与装夹方向距起点15～19 mm最大应变曲线的上升段均匀变化，间接证明了厚度减薄符合正弦规律的正确性。装夹方向和管口方向两端位置附近对应底部变形区，最大塑性应变变化小，趋势平缓。最大塑性应变距起点12.42 mm位置对应圆弧过渡区，变形最剧烈，最大塑性应变也最大。图10所示为成形波纹区域（底部变形区Ⅰ、斜面拉伸区Ⅱ和圆弧过渡区Ⅲ）。

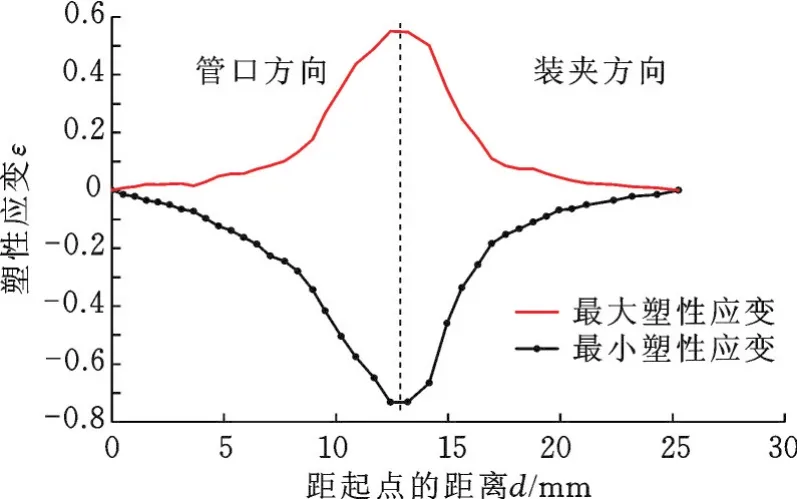
图9 仿真成形件的最大塑性应变和最小塑性应变Fig.9 Predicted plastic strain between a minor plastic strain and major plastic strain of the forming path

图11 所示分别为成形件外部和内部的等效塑性应变。工具轮与管内壁之间接触成形，塑性应变的最大值出现在管内表面上，管外表面相对管内表面等效塑性应变小16%。

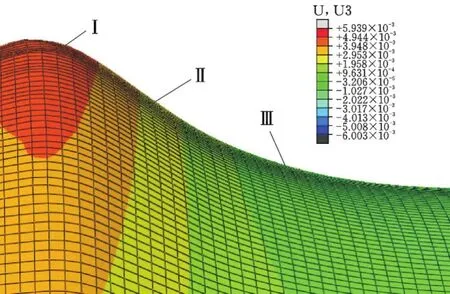
图10 成形波纹区域分布Fig.10 Distribute of forming corrugated area

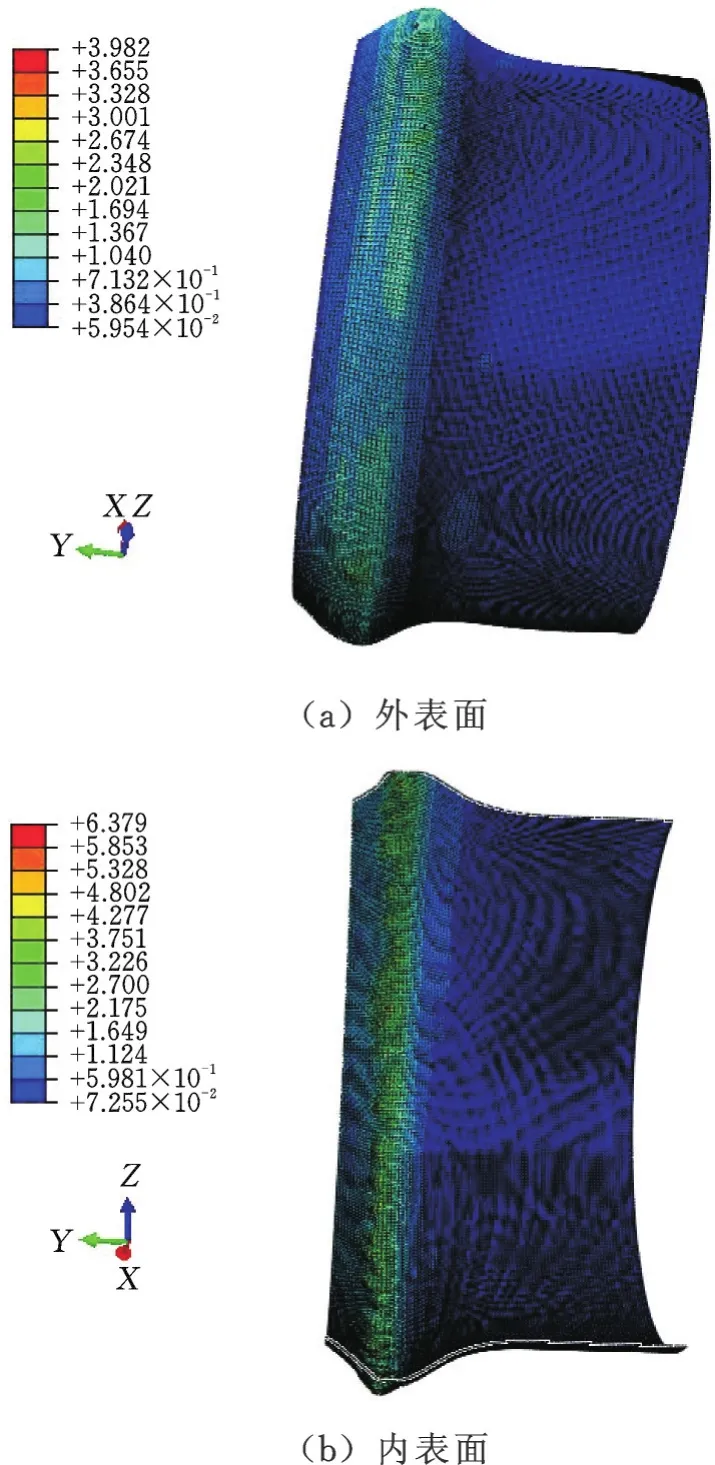
图11 成形件等效塑性应变云图Fig.11 Equivalent plastic strain distribution after formingaexteriortubesurfaceandbinteriortubesurface

管壁内外表面6个高斯点的等效塑性应变随时间变化曲线如图12所示。6个高斯点的历程时间是17 s，对应增量成形过程中的两个不同成形瞬间，工具轮分别进行了6次层进给。由于金属波纹管的成形经过多层轨迹的累积成形，因此塑性应变的变化是多次的，并且塑性应变在成形工具轮多次层进给成形中逐渐增大。层进给成形管壁过程中，当工具轮离开高斯点，塑性应变曲线随时间变化很小。每对高斯点位于同一横截面上，塑性应变的增大也就发生在每对高斯点的同一时刻。塑性应变增大的幅度也与工具轮每次层进给量有直接关系。

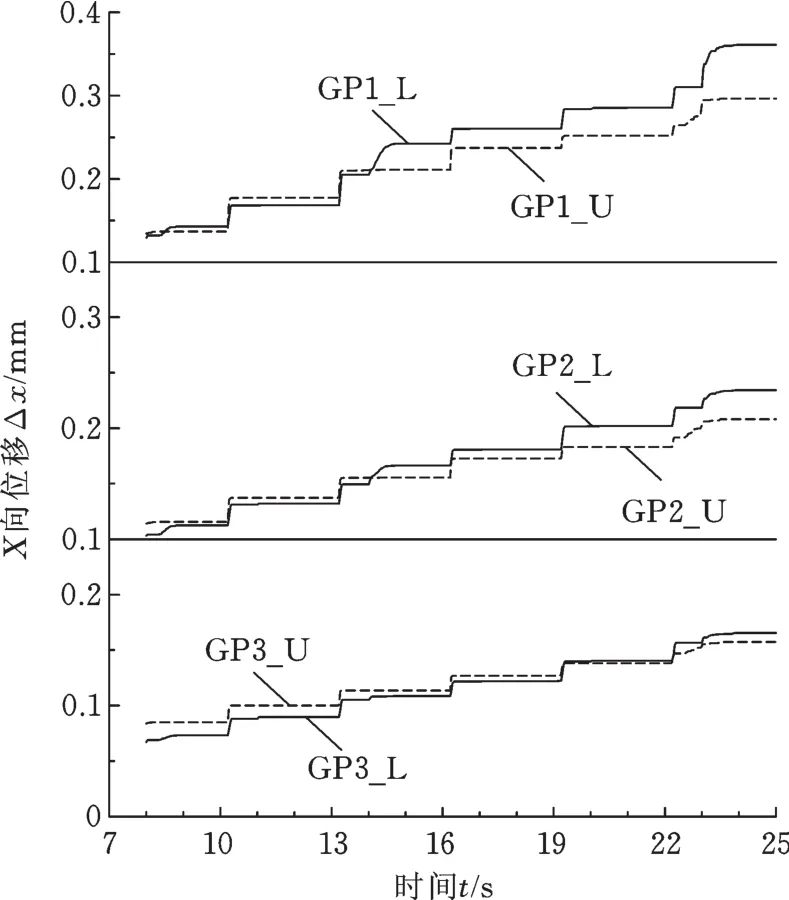
图12 仿真成形管壁6个高斯点等效塑性应变曲线Fig.12 Evolution of the equivalent plastic strain measured in six different Gauss points of the tube wall

4 实验验证

4.1 波纹管增量成形实验装置

采用CA6140车床进行金属波纹管成形，测力装置采用Kistler⁃9257三向压电晶体式测力仪、Kistler5070电荷放大器和北京波普数据采集处理系统，如图13所示。其中，测力仪量程为0～5 000 N，数据采集处理系统的采样频率为2 000 Hz，采样时间为30 s。润滑油选用福斯RENO⁃FORM FW 10S。工具轮材料为CrWMn，并且进行调质处理，如图14所示。工具轮尺寸、管材毛坯材料与尺寸、层间距、转速、进给速度、成形件尺寸都与有限元模型相同。成形后的金属波纹管样件如图15所示。

图13 增量成形测力装置Fig.13 Force measuring device of incremental forming

图14 成形工具轮装置Fig.14 A forming tool of metal tubes

图15 成形件Fig.15 Formed part

4.2 成形分力的测量

实验金属管单点增量成形波纹管过程中的3个方向分力如图16所示。实验增量成形样件过程中，X向分力Fx从初始时间开始经历一段上升区间后逐渐达到平稳状态，之后在稳定曲线上下波动，Fx比Fy、Fz大，验证了有限元模型的正确性。仿真和实验的3个方向分力都是经过一段上升区间后，在稳定曲线上下波动，且Fx比Fy、Fz大。

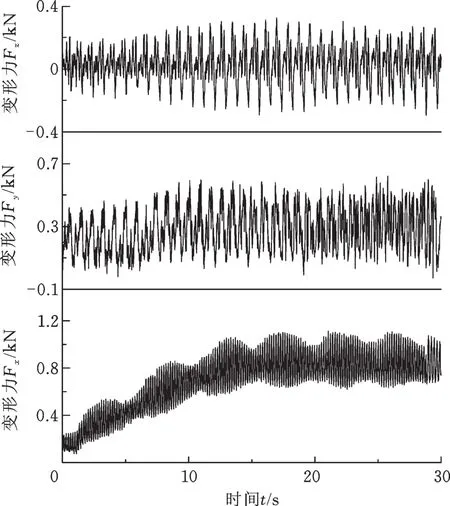
图16 三向成形力实验数据分布图Fig.16 Evolution of the experimental forming tool force measured in three directions

表4、表5所示分别为仿真和实验的平均成形力和最大成形力，有限元模型和实验测量的三向成形分力结果误差在可控范围内，进一步验证了有限元模型的准确性、可靠性。

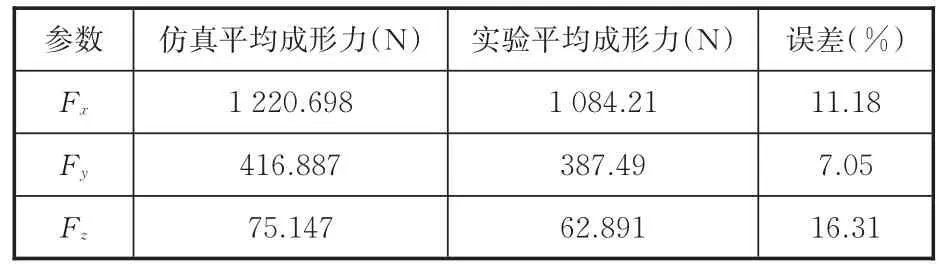
表4 仿真和实验的平均成形力Tab.4 Simulation and experimental data of average forming force

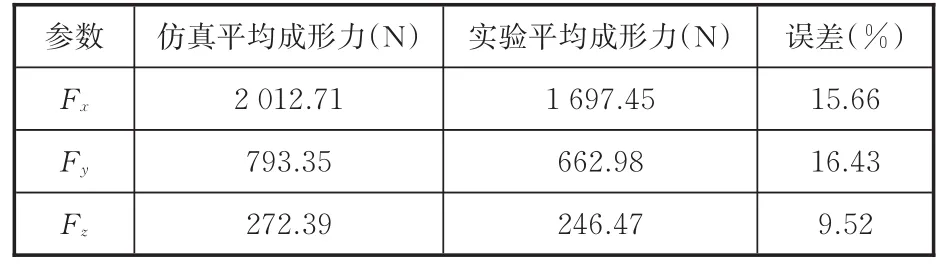
表5 仿真和实验的最大成形力结果对比Tab.5 Comparison between simulation and experimental data of maximum forming force

由于受机床振动、芯轴和金属管装配的配合公差、卡盘装夹工件配合圆度、工具轮芯轴弹性变形、机床进给误差、测力仪与机床装配效果、润滑条件、刀架装配效果的综合影响，实验测量到的3个方向分力在稳定后的一定范围内波动，且实验中测量到的三向分力与仿真模型提取的三向分力相比略小。

4.3 工艺参数对表面质量和波纹高度的影响

金属管增量成形过程中，层间距增大，管壁材料的应变随之增大，管壁加速变薄，层进给成形能力随之降低，并且对成形管壁表面质量产生影响，不合适的层间距会在管内壁产生螺纹状缺陷，成形后会存在大小不一的金属碎屑；主轴转速过高，会导致扩径发生，主轴转速过低，导致管壁材料变形过程不均；轴向进给速度也会对金属管增量成形产生影响，轴向进给速度过大，易导致与成形区接壤处管壁破损，轴向进给速度过小，易导致管壁起皱。为了研究层间距z、主轴转速n、轴向进给速度vy对成形质量的影响，设计表6所示的单因素工艺参数实验。

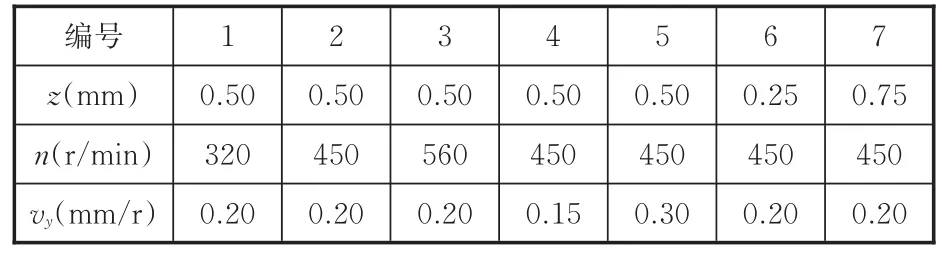
表6 工艺参数Tab.6 Process parameters

对7组工艺参数进行金属管增量成形实验，得到工艺参数对增量成形波纹高度的影响，如表7所示。由表7可知，主轴转速n对波纹高度的影响最大，其次是层间距z，轴向进给速度vy对波纹高度的影响不明显。主轴转速过大，会导致管壁的应变增大，同时高的主轴转速会产生大的离心力，导致扩径发生，最终的波纹高度偏大于理论值。过大的层间距会使管壁加速变薄，层进给成形能力也会随之降低，导致波纹管高度偏小于理论值；过小的层间距会导致工具轮与管壁接触范围变小，管壁材料的塑性变形不完全，管壁没有完全塑性变形，在成形完成后产生回弹变形，从而导致波纹高度的偏小于理论值。根据7组工艺参数实验，z=0.25 mm、n=320 r/min、vy=0.2 mm/r时的金属波纹管单点增量成形质量较好，波纹高度精度较高，不会出现破裂和起皱现象，并且成形后金属碎屑较小。

表7 不同工艺参数成形的波纹高度Tab.7 Corrugated height of different process parameters after forming

4.4 成形件波纹高度的测量

金属波纹管单点增量成形后，管壁上波纹形状尺寸是衡量波纹管加工质量的一项重要指标。因此，根据工艺参数实验，采用z=0.25 mm、n=320 r/min、vy=0.2 mm/r这组优化的工艺参数进行增量成形。加工完成后，使用基恩士VHX⁃5000三维显微系统测量成形件波纹高度。测量得到的实验数据与采用相同工艺参数进行仿真模拟数据如图17所示。由图17可知，仿真和实验得到的波纹高度数据整体分布一致。经过测量，仿真和实验数据在距起点8.65 mm位置处误差最大，最大误差为0.532 mm，最大误差百分比为16.78%，则有限元模拟与实验建立的金属波纹管增量成形结果是可靠的和正确的。

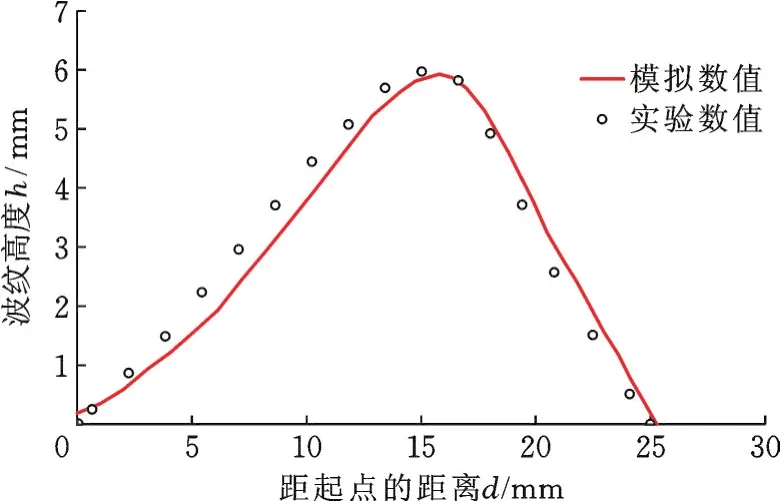
图17 波纹成形高度模拟数值和实验数值Fig.17 Simulation data and experimental data

5 结论

（1）将单点增量成形技术引入金属波纹管成形过程，提出了一种基于增量成形技术的金属波纹管成形工艺，并通过有限元模拟分析了金属管增量成形过程。

（2）通过分析仿真增量成形三向分力数据可知，X向分力Fx是管壁变形的主要成形分力，且经过一段上升区间后在稳定曲线上下波动；初始成形时，应力集中在工具轮和管壁接触区域，成形完成后，管壁变形区边缘处有较大的应力集中；当工具轮施加载荷于某一高斯点时，该点材料的变形位移数值变化较大，当工具轮离开时，该点变形位移增量趋势变小，并且当管壁成形为斜壁后，该点的变形位移变化趋势会大大降低；斜面拉伸区和圆弧过渡区材料的塑性应变大，该区域为管壁容易发生过度减薄和断裂，从而影响成形质量。

（3）搭建了金属管单点增量成形实验平台，通过金属管单点增量成形波纹管实验，验证了有限元模型的准确性和鲁棒性，进一步验证单点增量成形波纹管工艺的可行性，并对优化单点增量成形波纹管工艺方法有借鉴参考意义。