短纤维与基体的界面应力传递分析及界面刚度预测*

2018-11-09郭灿胡龚高

特种结构 2018年5期

郭灿胡龚高，2

（1.重庆大学土木工程学院 400045；2.山地城镇建设与新技术教育部重点实验室（重庆大学） 400045）

引言

纤维增强复合材料的剪滞模型最早由Cox［1］在1952年提出，该理论假定基体和纤维的接触面是理想界面。之后很多的研究者将剪滞模型应用到复合材料的应力传递研究中。Shetty等［2］利用剪滞模型在分析单根纤维拔出试验时估算复合材料的界面应力，刘永胜［3］在界面理想的情况时理论分析了复合材料的应力传递，Gao［4］等研究了界面完全粘结时的基体及纤维的应力分布。为了考虑界面的不完全粘结，使模型更加真实，有研究者在研究复合材料的过程中用不同的模型模拟界面，高庆等［5］在分析修正传统剪滞模型时的界面应力传递，通过有限元验证修正剪滞模型的必要性。王坎盛等［6］在经典剪滞理论的基础上利用内聚力模型表征界面的力学行为得到复合材料的应力传递。目前描述复合材料的界面的力学行为主要有线性材料模型［7］、三相材料模型［8］和内聚力模型［9］，其中内聚力模型是研究复合材料界面的主要手段，它表征的是基体与纤维的分离量与界面应力的关系，模拟了界面的硬化，软化，直至破坏的过程，能较好地模拟纤维与基体间界面的力学行为，因而在研究短纤维复合材料上得到广泛的应用。目前的内聚力模型主要有双线性应力位移法［10］、梯形应力位移法［11］、多项式型应力位移法［12］三种。其中双线性应力位移法能够较好地模拟界面的力学性能，已有人利用该模型模拟了纤维拔出，宗要武等［13］在有限元分析中引入内聚力模型模拟了钢纤维增强水泥基材料的界面荷载传递。本文在考虑基体正应力的情况下，利用剪滞理论，引入双线性应力应变位移法模拟界面的滑移关系，推导出纤维应力分布与界面刚度及材料参数的关系。最后从理论上讨论界面刚度对纤维应力分布的影响；利用试验的相关数据，求得界面刚度，通过与王坎盛等［6］的结果比较发现基体正应力对预测界面刚度的影响较大。

1 界面应力传递的理论推导

1.1 双线性cohesive模型

线性张开应力位移法则最初是由Mi等［14］提出的一种简单而有效的内聚力模型，双线性模型被普遍应用于有限元分析软件中进行计算分析，与其他张开位移关系相比，双线性张开位移关系模型简单有效，能较好地与有限元算法相适应。本文应用该模型模拟基体与纤维之间界面的力学行为，其界面切向应力与分离量的关系如图1所示。

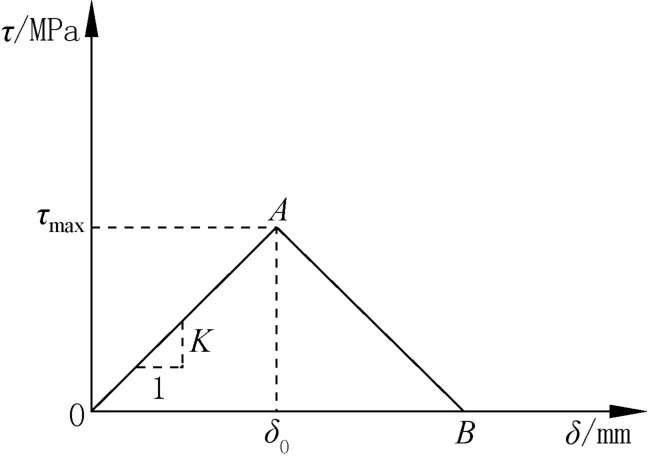
图1 双线性模型Fig.1 Bilinearcohesivezonemodel

对于双线性应力位移关系，切应力达到最大值之前，切应力随着分离量线性增长，即在材料未达到其自身的开裂强度之前，材料仍处于线弹性阶段。随之当张开应力超过最大值之后（δ0≤δ≤δf），材料出现损伤，随张开位移的增大而线性减小，直到τ趋于0，材料完全破坏。本文只考虑线弹性部分。

1.2 剪滞模型

建立如图2所示的应力传递的简化图，其中xoyz为空间坐标系，该模型长度为L，纤维所在位置长度为2Lt，半径为a，受到应力荷载为σ，该模型在空间上为轴对称模型。

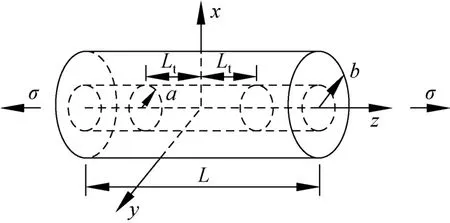
图2 应力传递分析模型Fig.2 Modeloftransferanalysisforstress

在代表性单元中，采用柱坐标系，其平衡方程为：

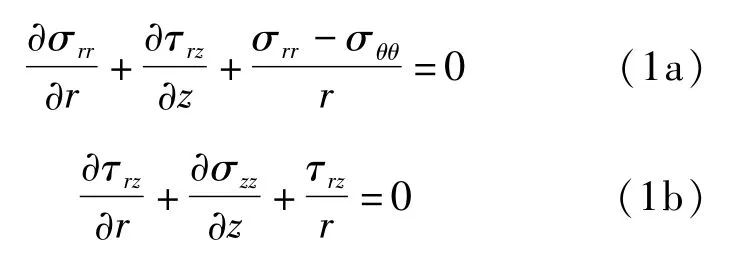
根据文献［4］可知纤维与基体的正应力满足方程式：

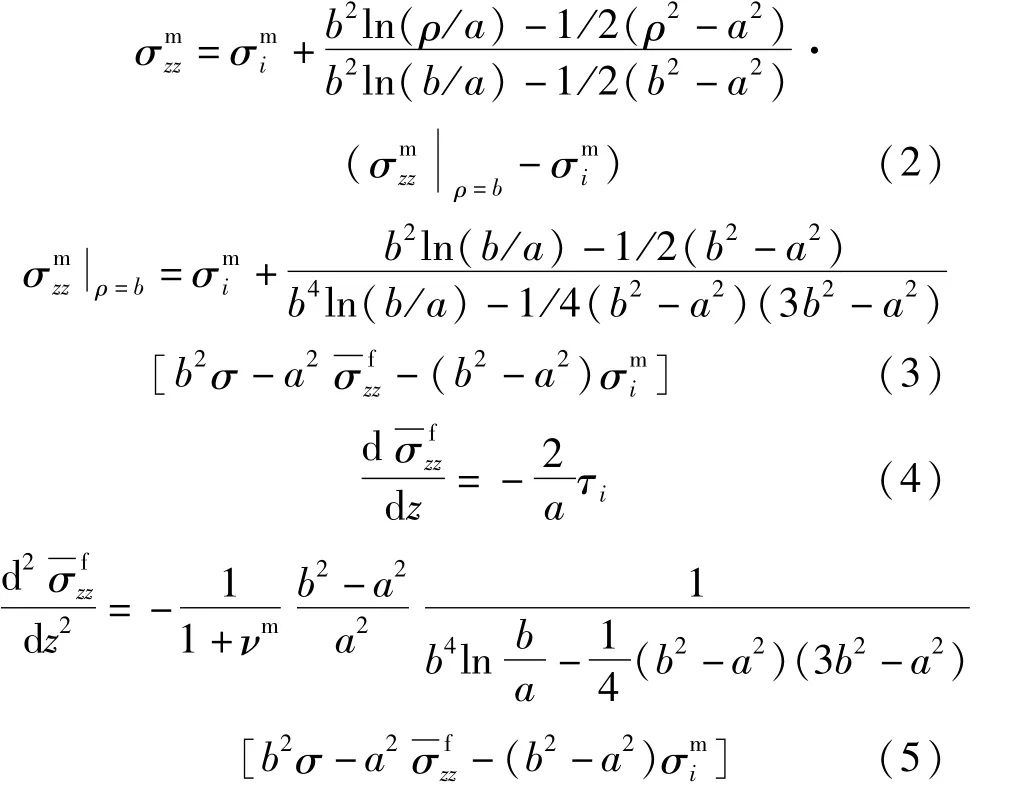
1.3 引用双线性cohesive模型

在工程实际中，由于在制作纤维复合材料的过程中，纤维与基体之间难免会有各种缺陷使得界面不完全粘结，而cohesive模型已被许多学者用来模拟复合材料界面的不完全粘结，即基体和纤维在界面（－Lt≤z≤Lt，ρ＝a）上存在分离量δ：

对式（6）两边求导得到纤维与基体在界面上的应变关系：

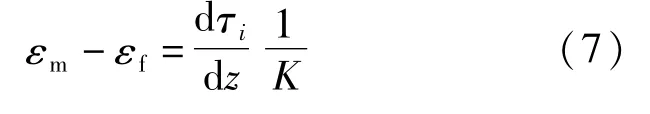
由于纤维只受轴向应力的作用，可得在r＝a处的应力应变关系式：

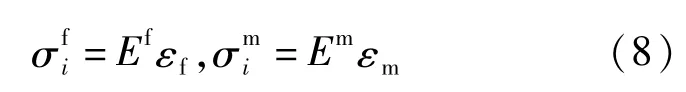
又因为纤维的横截面积很小，界面上的正应力可以用平均正应力取代，把式（8）代入式（7）得到基体与纤维在r＝a处的正应力关系：

然后对式（4）求导可得：

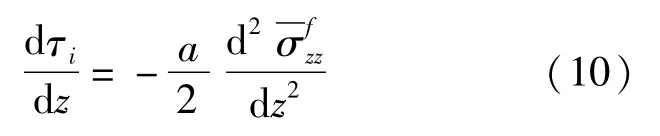
将式（9）、式（10）代入式（5）得到有关纤维正应力满足的方程：

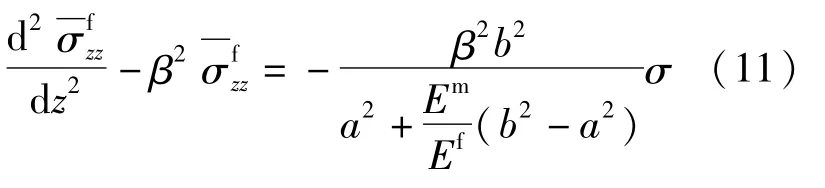
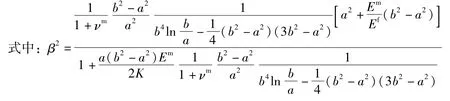
由式（11）求得纤维的平均正应力：

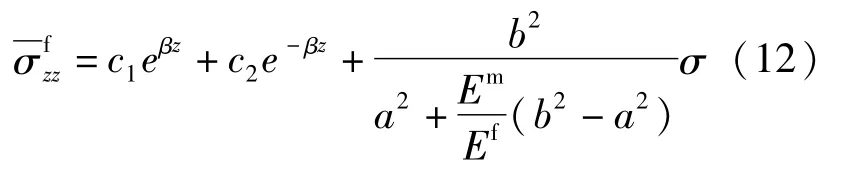
再把式（12）代入式（4）得到纤维在ρ＝a处的切应力：

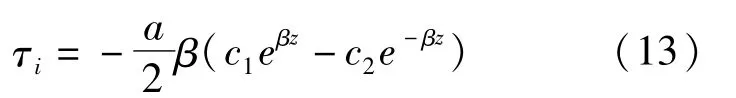
在这里沿用文献［6］的假定，假定纤维末端没有应力传递，因而有边界条件＝0 代入式（12）得到c1、c2：

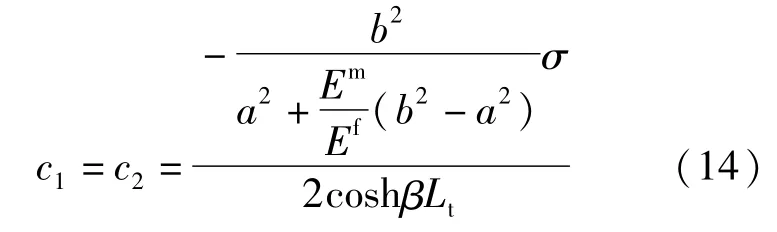
将c1、c2代入式（12）、式（13）得到：

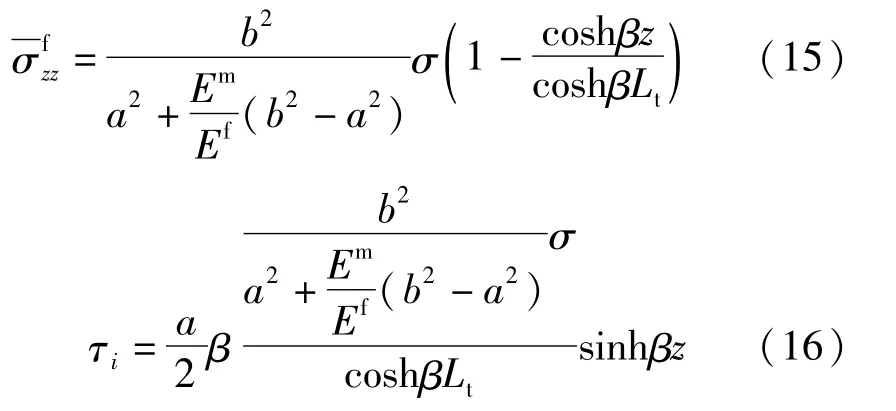
把式（15）、式（16）代入式（9）得到：

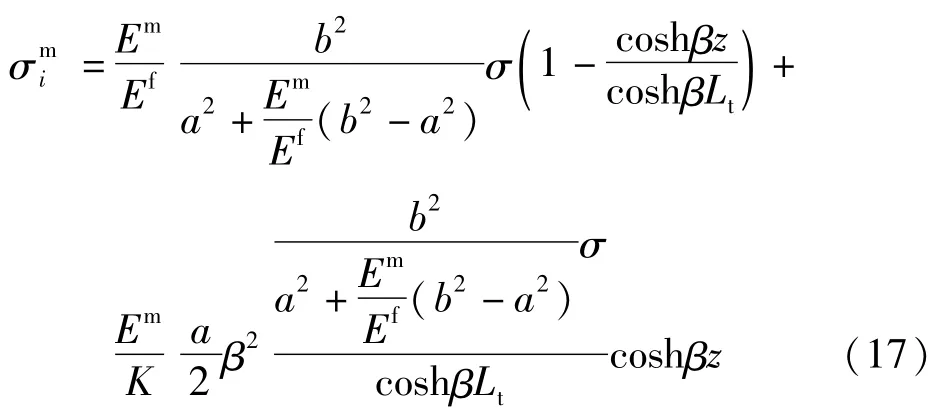
最后把式（17）、式（15）、式（3）代入式（2）可以得到有关基体正应力的表达式为：

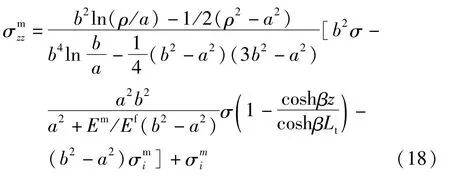
由式（15）、式（16）可以求得纤维正应力的最大值在z＝0处，而纤维切应力的最大值在z＝Lt处，纤维的最大正应力和最大切应力分别为：

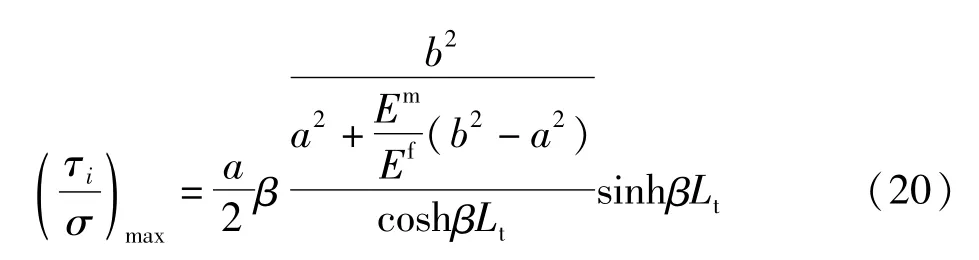
文献［6］计算了不考虑基体正应力的纤维应力分布，式（19）、式（20）是通过考虑基体正应力所得到的纤维正应力分布最大值，下面对比分析两者所预测的界面刚度的区别。

界面刚度取文献［6］中K＝1855.35MPa／mm。材料为亚麻纤维和环氧树脂，参数如下所示［16］：a＝0.15mm，b＝1mm，Ef＝10000MPa，Em＝3322MPa，νm＝0.39，σ＝33.22MPa。所得结果如图3、图4所示。

图3 纤维轴向正应力的最大值随纤维长度的变化Fig.3 Maximum of axial stress for fiber to the length of fiber

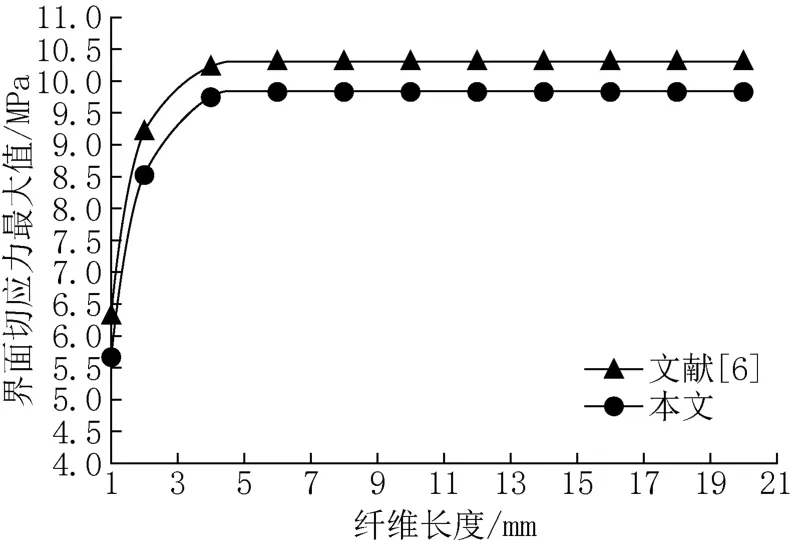
图4 界面切应力最大值随纤维长度的变化Fig.4 Maximum of interfacial shear stress for fiber to the length of fiber

由图3、图4可知，在界面刚度为K＝1855.35MPa／mm时，在不同的粘结长度下，根据式（19）所求得的纤维正应力最大值较文献［6］的小，差别在10%以下；根据式（20）求得的界面切应力较文献［6］的大，差别也在10%以下。

2 分析与讨论

2.1 界面刚度对纤维应力分布的影响

取不同界面刚度K，2Lt＝10mm，根据式（15）、式（16），分别得到纤维正应力、纤维切应力沿纤维轴向分布的情况，如图5、图6所示。在不同的界面刚度K的影响下，得到纤维应力分布的曲线，K＝∞时，纤维基体理想粘结。显然，当K较小时，纤维正应力和纤维切应力的分布变化受到K值的影响明显，且纤维正应力随纤维长度的增大而减小，在z＝0时，纤维正应力最大，在z＝Lt时，纤维正应力为0，即满＝0；纤维切应力刚好相反，且在z＝0时，纤维切应力为0。由图6可知，随着K值的增大，纤维正应力也相应增大。所给相同的外界荷载，在任意的纤维位置，理想粘结时的纤维正应力大于非理想粘结时的纤维正应力。

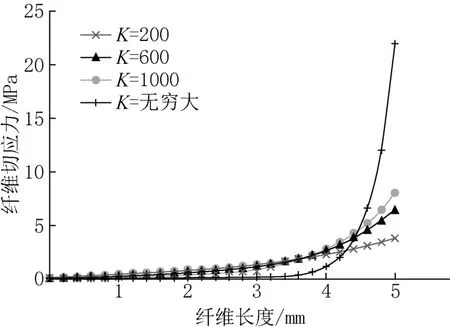
图5 不同刚度下纤维的切应力分布Fig.5 Distribution of shear stress of interface with different interface stiffness

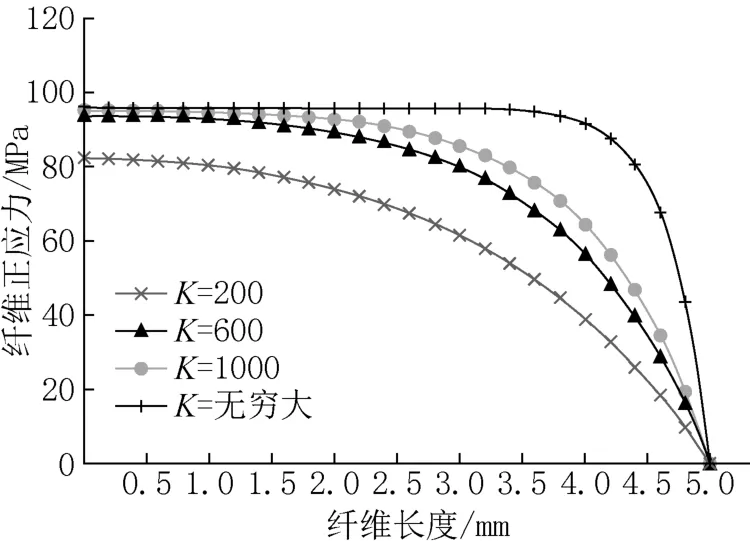
图6 不同刚度下纤维的轴向正应力分布Fig.6 Distribution of axial stress of fiber with different interface stiffness

2.2 纤维长度对极限应力的影响

在单丝断裂试验［15］中，发现纤维中部首先发生断裂，之后随着外加应力荷载的增大，纤维多次发生断裂。为了从理论上验证该现象，假定当纤维应力达到极限应力时，纤维发生断裂，即在同一根纤维中，复合材料受单向拉伸时，纤维最先断裂在纤维中间（因为纤维正应力最大值在纤维中间）。利用文献［16］的参数：纤维的极限应力＝191MPa。把纤维长度作为横坐标，外加极限应力作为纵坐标，取不同的界面刚度，根据式（19）得到外加极限应力与纤维长度的曲线关系如图7所示。

图7 外加极限应力随纤维长度的变化关系Fig.7 Change of the exert ultimate stress with fiber lengths

由图7可知当确定纤维的极限应力时，外界给的极限应力随纤维长度的增大而减小，当界面刚度越小时，这种变化越明显；纤维首次断裂在纤维的中部，之后随着纤维长度减小，应力重新开始分布，直到下一段纤维的应力达到极限值时，纤维继续出现断点；而当纤维长度减小到一定值时，纤维越难断裂，这从理论上解释了单丝断裂试验［16］过程中的现象。

2.3 界面刚度的确定

单丝断裂试验［15］即纤维在纤维正应力最大值时首先发生断裂，之后随着应变荷载的增加，纤维逐段断裂，在每一次纤维发生断裂后，断点附近应力值突减，轴向最大应力值也相应减小，纤维中的应力重新分布。继续加载过程中，纤维轴向应力才会增大，直到发生新的断裂。运用式（15）预测了文献［16］实验中的界面刚度。参数同2.2节所示，纤维长度2Lt＝10mm，在实验中当外界施加应变达到2.1%时纤维首次发生断裂。代入式（19）求得β＝0.74，继而得到K＝408MPa／mm；如果不考虑基体正应力影响，K＝1855.35MPa／mm［6］，由此可知，是否考虑基体正应力，对所预测的界面刚度K的影响较大。