基于柔度矩阵主对角斜率的结构损伤识别方法*

王立宪 周宇 狄生奎 吴长

（1.兰州理工大学西部土木工程防灾减灾教育部工程研究中心 730050；2.兰州理工大学甘肃省土木工程防灾减灾重点实验室 730050）

结构损伤多由于设计和建造缺陷或使用不规范等原因导致混凝土开裂、钢筋锈蚀等多因素非线性叠加，损伤进而会体现在结构自振特性的退化上，并可通过结构局部或整体刚度下降来描述，良好的结构损伤识别指标可以定性、定位、定量的描述结构损伤［1］。Pandey A K和Biswas M提出柔度差法，采用损伤前后柔度矩阵做差得到柔度差矩阵，通过模型试验及数值算例验证柔度矩阵用于梁结构损伤识别的有效性［2－3］。Aktan A E和Zhao J均通过算例和实验验证了柔度指标相比于频率和振型指标对损伤诊断有更好的敏感性［4－6］。柔度矩阵可通过较低阶模态参数获取较高的精度，较高阶模态参数对柔度矩阵贡献反而渐小，因此柔度矩阵类损伤指标可避免大量运算和有限元建模修正，诸多学者据此对基于柔度矩阵类损伤指标做了大量研究［7－10］。Ko等提出柔度矩阵改变率指标作为损伤诊断指标［11］。孙宗光等提取损伤前后柔度矩阵对角元素之间的比值求柔度矩阵变化率，用来识别斜拉桥损伤位置［12］。荆龙江和项贻强提出利用柔度矩阵主对角元素的变化绝对值判定大跨斜拉桥损伤位置［13］。曲率指标是对曲线平坦程度的衡量，包含二阶导数以及平方项可放大损伤处数值差异。Zhang Z和Aktan A E提出柔度曲率的结构损伤识别指标［14］。曹晖等提出模态柔度曲率差指标［15］，并在文献［16］里验证了模态柔度曲率差用于框架结构损伤识别。姚京川等提出柔度曲率改变率指标用于损伤诊断［17］。李永梅等提出柔度差曲率指标，并用于不同支承条件下梁结构损伤识别研究［18，19］。彭念等通过简支梁和两跨连续梁数值算例验证所提出仅基于损伤柔度曲率的损伤识别新指标［20］。

本文提出基于柔度矩阵主对角元素斜率的两个损伤识别指标：柔度矩阵斜率差（Flexibility Slope Difference，FSD）、柔度矩阵差斜率（Flexibility Difference Slope，FDS），通过提取损伤前后柔度矩阵主对角元素，按行顺序排成n×1阶列向量，柔度矩阵斜率差是对列向量求一次差分得到差分向量后做差得到，柔度矩阵差斜率通过对损伤前后列向量的差向量后求一次差分得到。通过简支梁不同位置、不同程度单点、两点和连续梁不同程度多点损伤工况，验证指标FDS和指标FSD识别效果并比较研究。

1 基于柔度矩阵斜率的损伤指标

斜率可以表示数列相对某一标准水平的倾斜程度和平均变化率。柔度矩阵内第i行第j列的元素为在单元j处施加单位力，单元i上产生位移，其主对角元素由相邻单元贡献叠加而成，相比其他非对角线元素有代表性。本文通过结合柔度矩阵对角元素与斜率提出柔度矩阵差斜率（FDS）指标、柔度矩阵斜率差（FSD）指标，构建方法过程如下。

1.1 构建损伤指标FSD和FDS

柔度矩阵可通过提取频率和振型向量构建［2］：

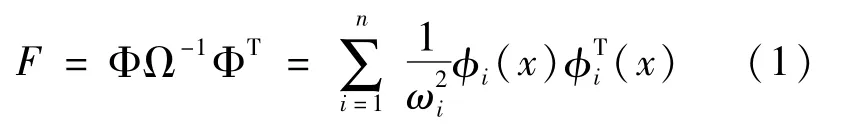
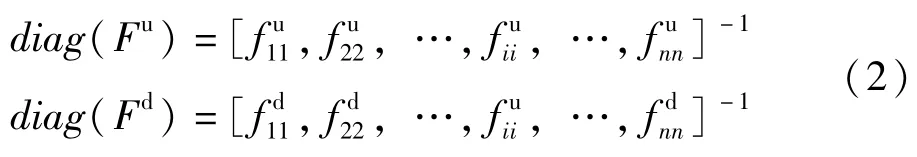
式中：上标d代表已损伤量；上标u代表无损量；diag（·）表示取括号内矩阵主对角元素按行顺序构成列向量，fii为构建列向量的柔度矩阵主对角元素。

1.2 构建柔度矩阵斜率差指标（FSD）

求损伤前后的柔度矩阵主对角元素斜率，即对diag（Fu）和diag（Fd）求一次差分，得到损伤前后主对角元素斜率列向量：

再求斜率列向量的差向量得：

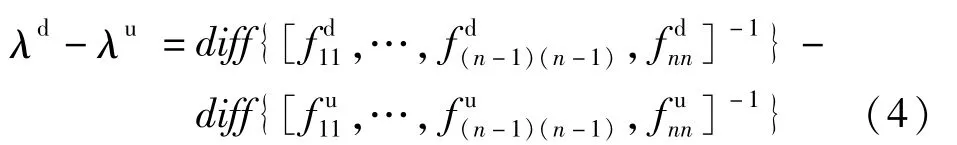
取式（4）式列向量中各元素绝对值得到柔度矩阵斜率差FSD指标：

1.3 构建柔度矩阵差斜率指标（FDS）

对损伤前后柔度矩阵主对角向量求差得：

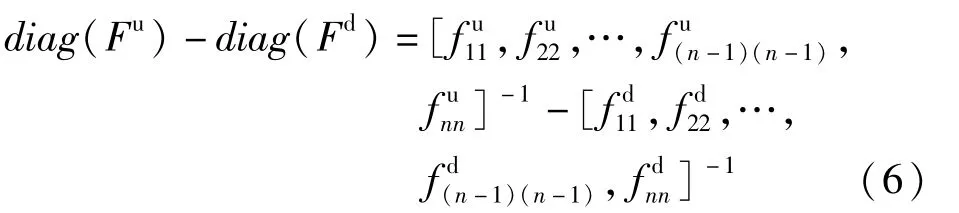
由式（6）各元素绝对值构成新的列向量Δ：

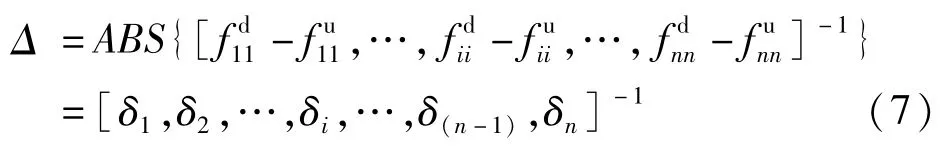
对差向量求一次差分，再取绝对值得柔度矩阵差斜率FDS指标：

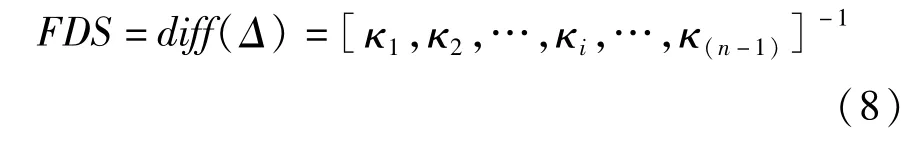
1.4 识别损伤

利用上述两种新指标，以x轴为单元号，y轴为损伤指标函数值，采用MatLab绘制损伤指标曲线图用于损伤位置判别和损伤程度评价。通过损伤指标曲线图的阶跃畸变点位置对损伤位置进行定位识别，利用损伤指标曲线图畸变幅值对损伤程度进行定量判别。

2 简支梁算例

2.1 模型概况和损伤工况

本文采用有限元软件MIDAS／Civil对简支梁进行损伤识别，采用梁单元进行模拟。建立的简支梁有限元模型基本参数：简支梁长为2m，材料弹性模量取33.141GPa，材料密度取2549kg／m3，材料泊松比取0.2，梁截面尺寸为0.15m ×0.2m，截面惯性矩为1×10－4。全梁共100个梁单元，从左至右依次排列，如图1所示。

图1 简支梁有限元模型Fig.1 Finite element model of a simple beam

简支梁各损伤工况通过降低单元弹性模量的5%、10%、20%、30%、40%方式来降低局部刚度，以此模拟局部损伤相应的百分数，单元质量不变且截面不削弱。各损伤工况汇总于表1。

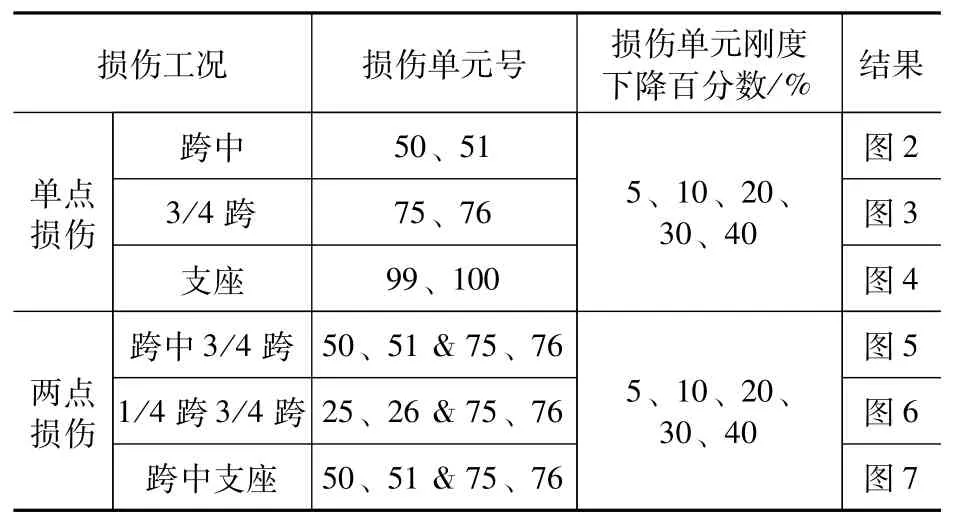
表1 简支梁损伤工况Tab.1 Damage cases of a simple beam

2.2 损伤识别结果分析

使用MIDAS／Civil提取简支梁模型损伤前后前三阶模态参数并作归一化处理，通过MatLab程序编写柔度斜率差FSD和柔度差斜率FDS公式，处理模拟数据，并绘制FSD和FDS曲线进行分析研究。损伤指标曲线图均以单元号作为横坐标、损伤指标值为纵坐标，通过损伤指标曲线畸变点标识损伤位置，以畸变幅值标识损伤程度。

1.单点损伤工况

简支梁单点损伤工况下（损伤工况见表1）损伤指标曲线如图2～图4所示。

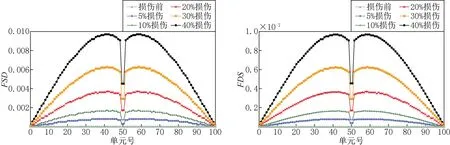
图2 简支梁跨中单点损伤工况Fig.2 One damaged element in the mid-span

通过图2比较FSD和FDS识别效果可以看出，两指标曲线均在跨中处第50单元出现阶跃畸变，且不同损伤程度呈现幅值差异，精确地识别了损伤的发生、损伤的位置，有效地标识了损伤程度的不同。尤其对跨中轻微损伤如5%时，该两种指标仍可较好的识别。

图3 简支梁四分之三跨单点损伤工况Fig.3 One damaged element in the 3／4th span

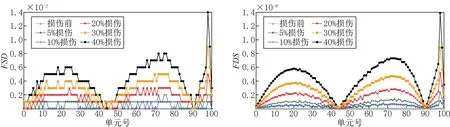
图4 简支梁支座单点损伤工况Fig.4 One damaged element near the support

由图3曲线形态特征可知，简支梁3／4跨单点损伤工况下，柔度矩阵主对角元素在第20单元和第65单元处出现变化率峰值。图3中FSD和FDS曲线在3／4跨（第75单元）处出现阶跃畸变点，精确地指出了损伤发生的位置，对损伤程度给出了定性判别。

由图4表明，在支座处出现不同程度损伤时，FSD和FDS曲线均在第18单元和第72单元附近出现峰值，FDS指标可以通过曲线阶跃畸变点精确地识别损伤发生位置，即支座附近（第98、第99单元），通过曲线阶跃畸变点处幅值标识出损伤程度差异。FSD指标仅在损伤超过20%时能准确标识阶跃畸变点位置。

单点损伤工况下，FSD相比于FDS曲线光滑、圆润，曲线数据不稳定点更少，识别精度更高。由图2～图4可以看出，在跨中、3／4跨、支座单点损伤工况下，FSD损伤指标幅值分别为9.8 × 10－3、5.8 × 10－3、1.4 × 10－3，FDS 损伤指标幅值分别为9.8 ×10－8、5.8 ×10－8、1.4 ×10－8。损伤曲线幅值从跨中向支座呈现出近似线性降低趋势，说明从对应梁跨中单元向对应支座单元的柔度矩阵主对角元素变化率下降。

2.两点损伤工况

简支梁在两点损伤工况下（损伤工况见表1）损伤指标曲线如图5～图7所示。

由图5中FSD和FDS曲线可以发现，跨中和1／4跨两点损伤的FDS和FSD曲线均在第49单元（跨中）、第76单元（四分之三跨）处出现峰值和阶跃畸变点，阶跃畸变点位置和幅值准确标识了损伤发生的位置和损伤程度。比较图5中FDS和FSD曲线，同一损伤程度下，跨中损伤处阶跃值大于1／4跨，其损伤识别敏感性优于1／4跨。

由图6中FSD和FDS曲线可看出，简支梁1／4和3／4跨两点损伤工况下，曲线在第26单元、第74单元处同时出现峰值和阶跃点，说明该两个指标在该工况下识别损伤位置和程度的整体效果良好。跨中处虽出现极小值，但未出现阶跃畸变点，所以并不影响损伤识别效果。

由图7中FSD和FDS曲线可知，跨中和支座处两点同时发生同等程度损伤时，曲线在跨中第50单元处出现阶跃畸变点，畸变位置明显且幅值大，标识了跨中不同程度损伤，但在支座附近阶跃幅值较轻微，识别效果相比跨中不明显。

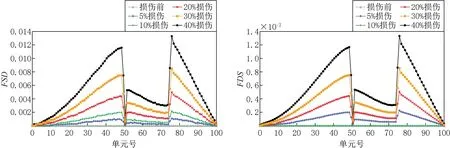
图5 简支梁跨中 ＆ 四分之三跨两点损伤工况Fig.5 Two damaged elements in the mid-span ＆ the 3／4th span

图6 简支梁四分之一 ＆ 四分之三跨两点损伤工况Fig.6 Two damaged elements in the 1／4th span ＆ the 3／4th span

图7 简支梁跨中 ＆ 支座两点损伤工况Fig.7 Two damaged elements in the mid-span ＆ near the support

两点损伤工况下，FDS指标曲线的平滑性和数据稳定性优于FSD指标曲线。参照单点损伤识别结果可得到同样结论，FSD和FDS两个指标识别损伤的敏感性由跨中位置向支座位置呈现降低趋势。

3 连续梁算例

3.1 模型概况和损伤工况

采用有限元软件MIDAS／Civil对连续梁进行损伤识别，采用梁单元进行模拟。建立的连续梁

有限元模型基本参数：连续梁尺寸为3×2.0m，材料及截面特性同简支梁算例。全梁共300个梁单元，从左至右依次排列，如图8所示。

图8 连续梁有限元模型Fig.8 Finite element model of a continuous beam

连续梁局部损伤的模拟方法与简支梁算例相同，以降低单元刚度实现。损伤工况见表2。

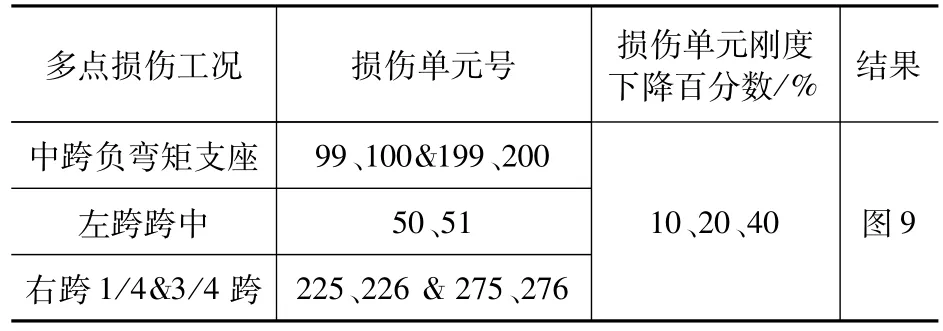
表2 连续梁损伤工况Tab.2 Damage cases in a continuous beam

3.2 损伤识别结果分析

连续梁多点损伤工况下（损伤工况见表2）损伤指标曲线如图9所示。

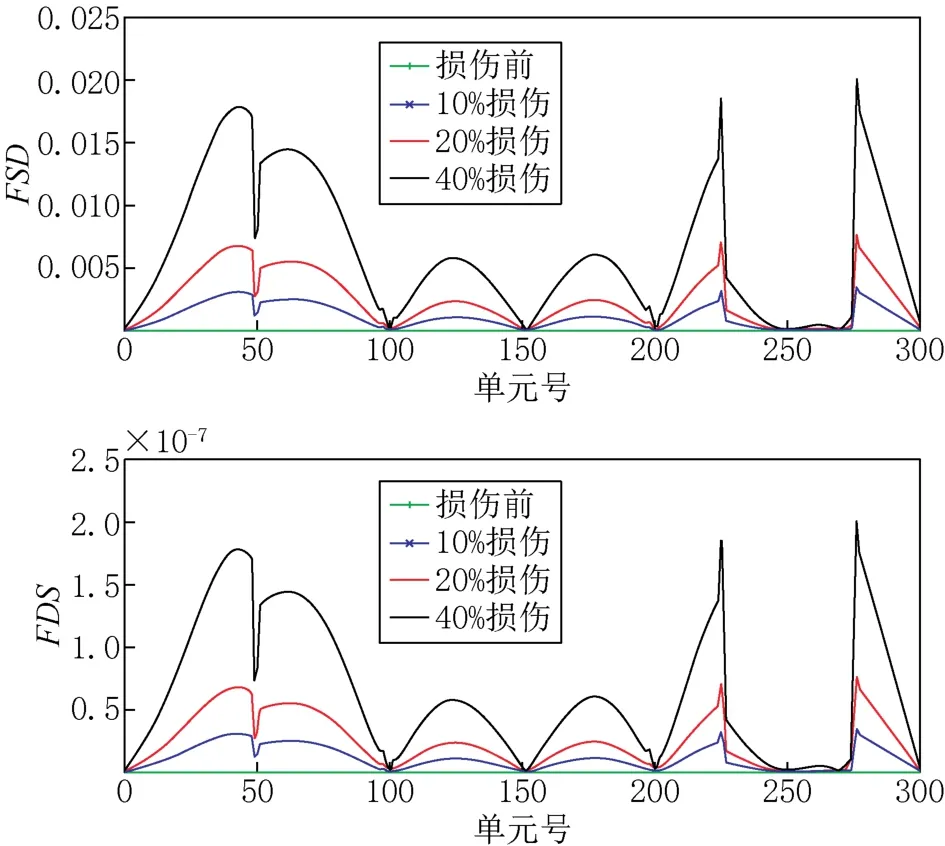
图9 连续梁多点损伤工况Fig.9 Multiple damaged elements in a continuous beam

通过比较图9中FSD和FDS指标曲线，可以看出两曲线形态特征差别不大，均表现在左跨跨中（第50单元）、右跨1／4跨（第225单元）和3／4跨（第275单元）出现明显阶跃畸变，在两负弯矩支座（第100单元和第200单元）处，指标曲线阶跃畸变轻微。FSD和FDS指标应用于连续梁多点损伤识别时，在支座处损伤识别敏感性较低，但可以精确识别非支座部位损伤的位置并定性判别损伤程度。

4 结论

本文提出对提取损伤前后柔度矩阵主对角元素，先进行一次差分再求差向量得到柔度矩阵斜率差FSD损伤识别指标，同时先求差向量后做一次差分得到柔度矩阵差斜率FDS指标。通过建立简支梁和连续梁算例，绘制FSD曲线及FDS曲线进行对比研究，验证所提出的FSD和FDS两个新损伤识别指标的识别效果。研究分析表明：

1.柔度矩阵斜率差（FSD）和柔度矩阵差斜率（FDS）均可作为简支梁结构单点、两点损伤识别指标和连续梁非支座处损伤识别指标，识别过程中可通过曲线阶跃畸变点位置精确标识损伤位置，并通过畸变曲线幅值大小定性判别损伤程度。

2.FSD和FDS两个指标对简支梁和连续梁非支座部位不同程度损伤诊断精确度高，行之有效。简支梁和连续梁从跨中向两侧支座呈现出指标识别敏感性下降趋势，对支座处轻微损伤识别精度较低。

3.在简支梁结构损伤识别过程中，FDS损伤指标曲线相对于FSD损伤指标曲线光滑，数据均匀稳定，识别精确程度相对较高。

4.本文所提出的柔度矩阵斜率差（FSD）和柔度矩阵差斜率（FDS）在计算工作量上较柔度曲率类指标少一次中心差分，用于快速判定损伤发生、定位最危险点具有一定优势。