基于高斯分布的检测算法在居民用电行为异常分析中的应用

刘丰威，胡文，陈臣

（广州供电局有限公司，广东广州，510620）

0 引言

当前在用户用电的过程中，存在窃电、欺诈等一系列问题，这些问题会导致电力损失，统称为非技术性损失NTL(Non-Technical Loss)。非技术性损失不仅仅会影响电力系统的正常运行，而且对于整个电网的调度也会产生显著影响，甚至由于窃电等行为的存在会引发安全事故。因此，对于电力企业以及电力系统而言会对用户的用电行为进行稽查。目前稽查用户行为异常主要靠人工进行筛选，而依靠人工筛选的工作量大、效率低等原因，如果考虑利用机器学习对居民用电行为进行分析，自动筛选出用电异常嫌疑比较大的用户，重点对筛选出的用户进行分析，减少其工作量。其中高斯分布的检测算法能够进行对用电行为进行分析，因此希望通过高斯分布的检测算法对居民用电行为异常进行分析。

1 居民用电行为异常分析常用算法分析

1.1 规则制定法

这是比较常用的一种方法，即通过历史经验或者对数据进行一定的处理并且得到阈值，并且制定一系列规则，在用户用电量在一定条件下高于该阈值的时候便自动判定为异常。

该方法优点为简单快捷，可以通过规则一步得出用电异常的用户或者通过阈值得到用电嫌疑用户，但是缺点也十分明显，即根据历史经验或者对数据简单处理的阈值可能不能精准的定位到实际的阈值。

1.2 聚类分析法

其基本原则都是： 希望族（类）内的相似度尽可能高，族（类）间的相似度尽可能低（相异度尽可能高）。常用的聚类方法有以下四种。

划分聚类：给定一个n个对象的集合，划分方法构建数据的k 个分区，其中每个分区表示一个族（族）。大部分划分方法是基于距离的，给定要构建的k个分区数，划分方法首先创建一个初始划分，然后使用一种迭代的重定位技术将各个样本重定位，直到满足条件为止。

层次聚类：层次聚类可以分为凝聚和分裂的方法；凝聚也称自底向上法，开始便将每个对象单独为一个族，然后逐次合并相近的对象，直到所有组被合并为一个族或者达到迭代停止条件为止。分裂也称自顶向下，开始将所有样本当成一个族，然后迭代分解成更小的值。

基于密度的聚类：其主要思想是只要“邻域“中的密度（对象或数据点的数目）超过某个阀值，就继续增长给定的族。也就是说，对给定族中的每个数据点，在给定半径的邻域中必须包含最少数目的点。这样的主要好处就是过滤噪声，剔除离群点。

基于网格的聚类：它把对象空间量化为有限个单元，形成一个网格结构，所有的聚类操作都在这个网格结构中进行，这样使得处理的时间独立于数据对象的个数，而仅依赖于量化空间中每一维的单元数。

1.3 基于高斯分布的检测算法

异常检测的样本数据，可能有标签，但通常正常状况的样本很多，异常状况的样本很少，并且出异常的原因通常也不尽相同。所以，可以只针对正常状况的样本建模。

但因为本文收集的用电量数据没有标签，则可以对所有的样本数据用一个模型建模，因为通常数据中异常状况的样本很少，对最终模型的影响很小。

通常样本数据是多维的，所在使用高斯分布来建模的时候，可以分别对每一维使用一个一元高斯分，或者是对多维使用一个多元高斯分布来描述正常状况的样本数据。

这样得到高斯分布模型对正常状况的样本计算得到的概率值就会比较大，对异常状况的样本计算得到的概率值就会比较小。

2 聚类算法与高斯分布检测算法在用户异常用电中的应用效果对比

2.1 聚类分析法应用效果分析

划分聚类是基于距离的，可以使用均值或者中心点等代表族中心，对中小规模的数据有效；而层次聚类是一种层次分解，不能纠正错误的合并或划分，但可以集成其他的技术；基于密度的聚类可以发现任意形状的族，族密度是每个点的“邻域“内必须具有最少个数的点，可以过滤离群点；基于网格的聚类使用一种多分辨率网格数据结构，能快速处理数据。

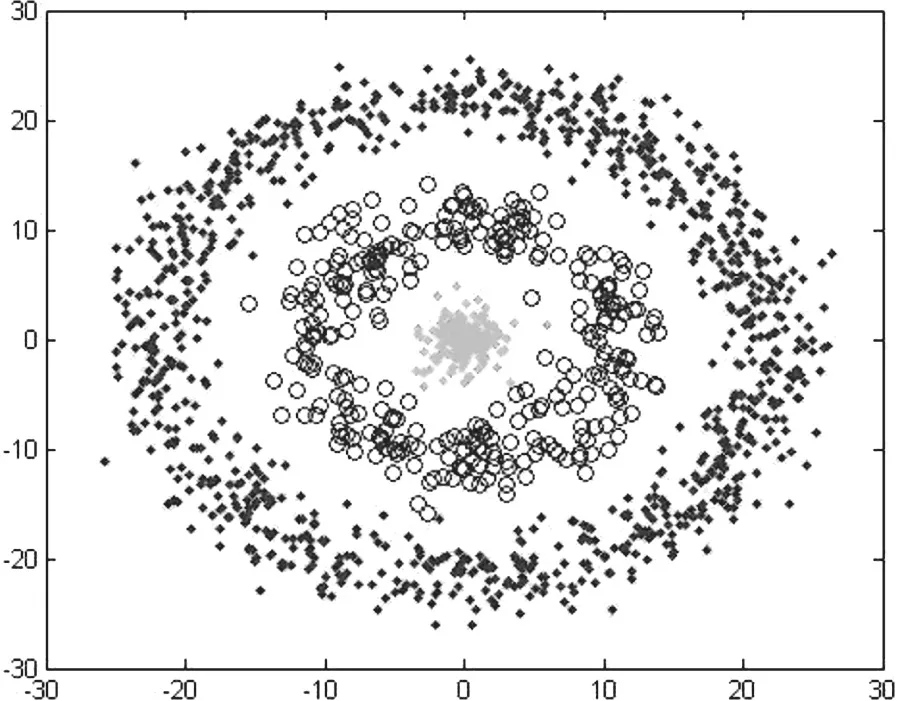
图1 多分辨率网格数据处理图

如图1可以看出，通过聚类分析可以将相似度较高的一组数据进行分类。

其有不需要对数据进行打标签，并且可以通过快速迭代完成分类的优点，但是如数据并没有清晰的分界，那么聚类分析算法将不能很好的应用。抽取普通居民用户约4000户，将其用电量做成散点图图2。

从图2可以看出，除了年用电量超过5万度的3个用户，其余用电量均分布在0-20000度，并且没有明显的分界。因此仅基于低压普通居民用电量数据较难应用聚类分析算法。

2.2 高斯分布检测算法应用效果

可以设定一个阈值，对一个新样本，使用训练得到的多元高斯分布模型计算概率值，如果得到的概率值比阈值小，就认为它是一个异常情况。

图2 居民年用电量分布图

下面我们观察居民用电量在不同区间的分布情况。

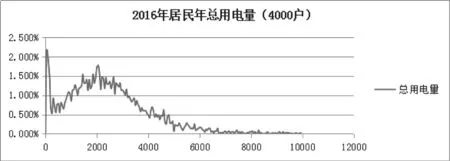
图3 2016年居民年总用电量

由图3可以发现，很多住宅基本没人住， 0度户需要除去，去除0度户后可以发现居民用电量分布基本符合高斯分布。

3 基于高斯分布检测算法的用电异常分析具体应用

高斯概率的分布函数为：

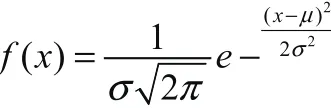
正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。

累积分布函数是指随机变量X小于或等于x的概率，用密度函数表示为：

3.1 数据选取及预处理

由于从计量自动化系统导出的数据如图4和图5所示。

由图可知，0度户占了绝大部分，因此需要先将0度户剔除，同时一年用电仅有200度以下的用户可视为没有人居住的用户，也需要剔除。最后得出2016年总用电量分布图如下，用柱状图方式表达，可以看到，总用电量分布基本上符合高斯分布。

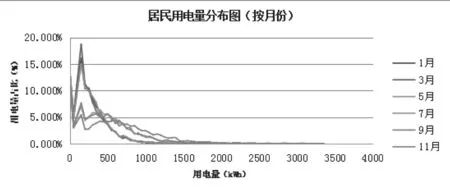
图4 居民用电量分布图

图5 居民年总电量分布图

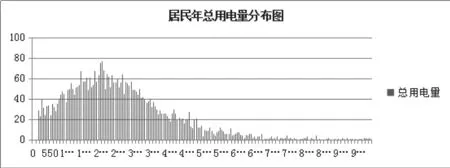
图6 居民年总用电量分布图

那么下一步可以进行高斯分布公式的计算。

3.2 高斯概率的分布函数的计算

根据已经处理好的数据，下一步需要对数据进行计算，求出高斯概率分布函数的参数。

第一步进行µ的计算，计算公式如下：

图7 理论分布、实际分布对比图

本文选取多于平均值5个标准差作为异常检测的阈值，即2555+5*1550=10305kWh。

确定好阈值后即可以随机选取台区，选取台区中居民用电，并且用电容量为4kWh的居民用户，将超过阈值的用户筛选出来并且按照偏离平均值的大小进行排序，根据该清单去现场进行稽查核实，提升工作效率。

4 结论

本文使用了基于高斯分布概率函数的异常检测算法，本算法可以根据样本自动确定异常阈值，同时定期更新样本可以获得新的异常阈值，不会因为整体用户群用电量发生改变就使算法失去意义。未来可以进一步辅助以聚类算法对居民用电行为进行聚类，可以进一步筛选出用电行为异常嫌疑较大的用户，同时辅助变压器过载信息，辅助历史用电突变情况等一系列信息进行判断。可以进一步精确定位居民用电异常的行为。相信未来随着算法的进步，机器学习分类、异常检测可以极大提升稽查工作效率。