激光光束的傅里叶分析实验模拟：基于SeeLight和MATLAB平台

刘隽宇

（山东省青岛第二中学，山东青岛，266100）

0 引言

信号的傅里叶分析的目的是在频域研究信号的特征，其中傅里叶分析的原理是任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。傅里叶分析方法不仅应用于电力工程、通信和控制领域中，而且在力学、光学、量子物理和各种线性系统等许多有关数学、物理、和工程技术领域中得到广泛而普遍的应用。

在激光领域，激光谐振器发出的基模谐振腔的横截面振幅分布，在通常情况下遵守高斯函数，此类光束称高斯光束。而由于高斯光束在激光应用中存在诸多限制，因此人们致力于探索性能更优的光束，如艾里光束等无衍射光束。2007年，艾里光束首先由 Christodoulides 研究组实验实现，实验现象表明：艾里光束除了具有无衍射和自愈特性外, 还具有自弯曲传输的奇异特性[1]。艾里光束的实现以及其奇异的特性因此很快引起了研究人员的广泛关注，人们纷纷开始研究艾里光束在各种介质下的传输特性。

随着对激光研究的深入，人们不止在时域关注激光的性质，通过频域上的观察，可以研究激光的单色性等性质。为了研究激光光束的频谱特性，采用傅里叶分析的方法可以方便快捷地获得光束在频域上的频率组成，为之后的性质研究打下基础。

1 理论研究

1.1 高斯光束实验理论

1.1.1 高斯光束

激光的横截面振幅分布满足高斯分布的光束称为高斯光束，这里假设高斯光束沿着z轴传输，束腰中心在坐标原点位置，那么z=0平面上的交叉功率谱为[2]：

其中，ω为角频率，0S (ω)为源光谱，0w为高斯光束的腰斑半径。

1.1.2 透镜的傅里叶变换性质

如图1所示，入射的光束首先沿直线传播，在遇到透镜之前经过一个衍射屏，产生了衍射光场。实验现象表明：当这个光场中包含很多不同的频率成分时，凸透镜的会聚作用使得衍射光场中拥有相同空间频率的光波成分将会聚集到透镜的像方焦平面上（如图1中的光线1和2，光线3和4的空间频率相同，它们经过透镜后分别会聚到A、B两点）。此时，在透镜的像方焦平面上安放一个观察屏，屏上显现的是衍射波场的空间频率分布，这种变换就是从空域到频域的变换，即光场的傅立叶变换。按此理论来说，当光场包含的频率成分较少或者只有一种频率时，映在观察屏的空间频率少量的点或者只有一个点。透镜像方焦平面上的光波复振幅分布 E (xf, yf)表达式如下（其中 T (u ,v)是t(x,y)的傅里叶变换）[2]

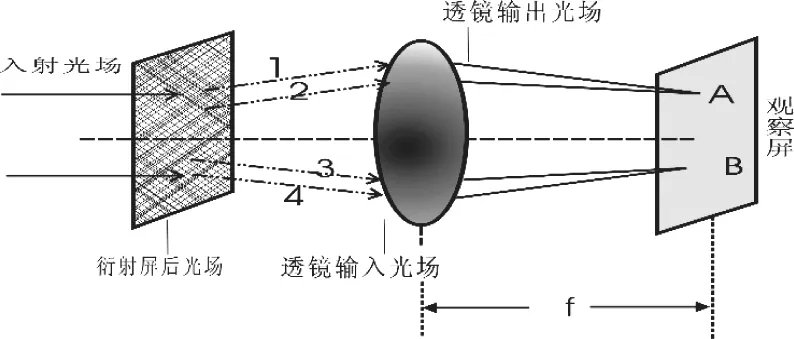
图1 透镜的傅里叶变换性质

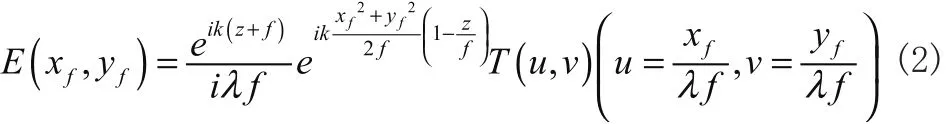
1.2 艾里光束实验理论

在量子力学框架下, 薛定谔方程被用来描述粒子和波的运动, 一维形式的薛定谔方程描述为[1]:

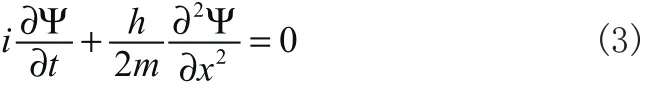
而在光学领域, 傍轴近似下光束的线性传输行为遵循以下衍射方程[1]:

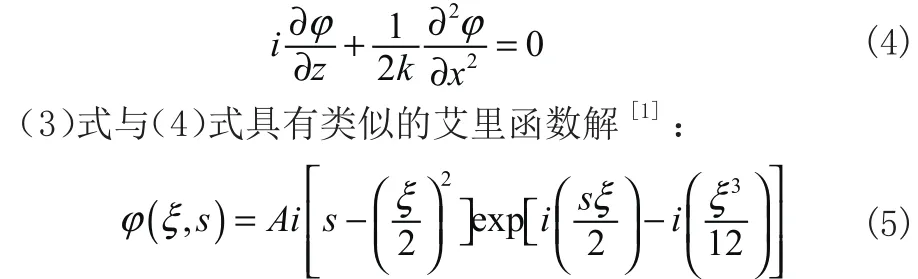
其中,Ai表示艾里函数,s=x/ x0是归一化无量纲横向坐标,ξ=z/k x0²为归一化传输距离, x0为选取的横坐标常量。

由于艾里光束携带无穷大的能量而不能收束,因此满足（5）式形式的艾里光束在现实中是不存在的，此艾里光束称之为无限能量艾里光束。然而，我们可以通过数学的方法对艾里光束进行“截趾”，在（5）式的入射光场上乘以一个指数衰减项exp(αs)(α>0为指数衰减因子)。以该新的光场为初始解形式,重新求解傍轴衍射方程,可得[1]：

由此表明遵循此式的艾里光束可以实际存在，称之为有限能量艾里光束。

类似地，我们还可以写出二维的艾里函数解[1]：

研究表明艾里光束在长距离、复杂的介质中具有优良的传输特性[3]，因此作为对比，我们可以分析其频域上的表现与高斯光束的不同，并分析由此造成的特性上的差异。而由于二维艾里光束是在两个维度上描述的光强分布，因此我们下一部分采用二维艾里光束进行模拟。

2 模拟仿真

2.1 基于SeeLight平台的高斯光束的傅里叶分析

实验条件：根据理论部分的描述，我们知道可以通过透镜模拟光场的傅里叶变换。根据图1的原理，基于Seelight光学系统虚拟仿真实验平台，放置实验装置如下图2所示。

图2 基于SeeLight平台的高斯傅里叶分析模拟图

运用控制变量法，分别改变波长，束腰半径，传输距离，透镜焦距的实验条件，依次得到仿真图像。

（1）实验1：当高斯光束的束腰半径较小时，焦距对结果的影响分析实验

实验条件：波长550nm 束腰半径0.01cm 传输距离20cm透镜焦距从15cm 依次以5cm的间隔递增。

实验现象：

图3 高斯光束经过透镜后的图像

实验结论：通过SeelLight的模拟，得到三个透镜焦距依次为15cm,20cm,25cm的振幅图像(如图3(a),(b),(c)所示。三幅图都表现出单一频点的特性，符合单一波长的高斯光束经过傅里叶变换后的幅频特性，不同之处是从三幅图中可以看出，随着焦距的增大，最后得到的图像上频点的直径也随之增大，这符合透镜成像的原理。

（2）实验2：高斯光束的束腰半径较大时，焦距对结果的影响分析实验

实验条件：波长550nm 束腰半径0.04cm 传输距离20cm透镜焦距从15cm 依次以5cm的间隔递增。

实验现象：

实验结论：增大束腰半径从0.01cm到0.04cm，得到三幅幅度的图像(如图4(a),(b),(c)所示，通过对比可以发现，三幅图都表现出了除中心光点以外的横纵轴亮线，符合单一波长高斯光束经过傅里叶变换后的幅频特性。通过与实验1的对比，我们可以看出，束腰半径增大时，通过透镜变换后越能体现高斯光束频谱特性的更多细节。

图4 高斯光束经过透镜后的图像

（3）实验3：波长对结果的影响分析实验

实验条件：波长550nm束腰半径0.04cm传输距离20cm透镜焦距25cm和波长632.5nm束腰半径0.04cm传输距离20cm透镜焦距25cm。

实验现象：

图5 高斯光束经过透镜后的图像

实验结论：从图5(a),(b)中可以看到，波长变长时的图像相比550nm，光斑大小没有变化，幅值稍微变小。根据傅里叶变换公式可以知道，傅里叶变换后的像函数与e^ (-iwt)有关，那么波长变长意味着w变小，-w则增大，e^ (-iwt)的实部和虚部在波动，但是 abs(e^ (-iwt))却保持恒定的值不变，因此单个波长改变，并不会影响傅里叶变换后的光强分布，只是幅值大小会稍微受影响。

2.2 基于MATLAB平台的艾里光束的傅里叶分析

通过MATLAB编程模拟艾里光束[4～5]，并使用自带的二维离散傅里叶变换函数fft2()对模拟的艾里光束进行傅里叶变换，在此基础上，通过改变衰减系数，观察不同实验条件下的实验现象。

（1）实验1：衰减系数较小时的分析实验

实验条件：衰减系数0.01，传播3000米。

实验现象：

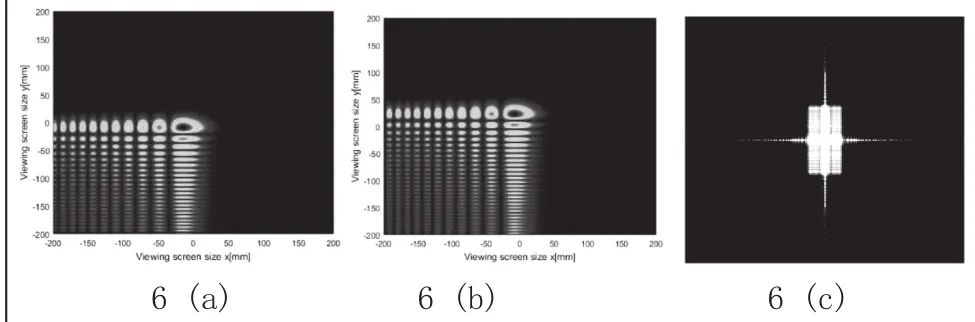
图6 艾里光束图像

实验结论：从图6(a),(b),(c)可以看出，艾里光束在传播一段距离后，其光束整体发生了偏移，这验证了艾里光束的自加速特性。从图6(c)艾里光束经过傅里叶变换后的图像可以看到，艾里光束的频谱图与高斯光束的有相似之处，如有相似的十字亮线以及中间亮斑，不同的是由于艾里光束除了主瓣以外，有多个旁瓣，这些旁瓣的存在在频谱图上的表现是产生了中心亮点以外的小亮点。

（2）实验2：衰减系数偏小时的分析实验

实验条件：衰减系数0.1，传播3000米。

实验现象：

图7 艾里光束图像

实验结论：当衰减系数增大时，艾里光束传输时的衰减增大，可以看到传输3000米以后图7(b)的光强图像艾里光束光强减弱，并且出现旁瓣间隔不清的现象。这直接导致其频谱图中心以外的亮点分布的区域范围变小，表明艾里光束频谱图频点在减少。

（3）实验3：衰减系数较大时的分析实验

实验条件：衰减系数1，传播3000米。

实验现象：

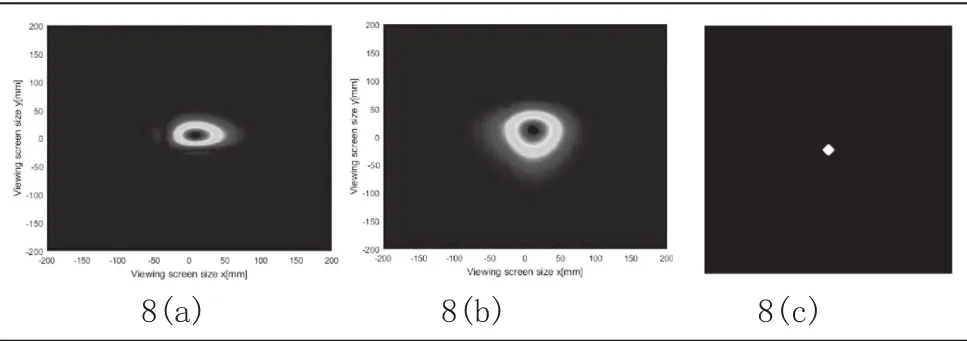
图8 艾里光束图像

实验结论：当衰减系数增大到1时，传输3000米后发现其光强图像变为图8(b)的形式，即变为类高斯光束，对其进行傅里叶变换，得出图8(c)只有一个亮点的图像，表面图8(b)的频谱图只有一个频点。

通过以上三个实验对比，可以发现，随着艾里光束衰减系数的增大，传输同等距离时，衰减系数小的艾里光束在传输过程中衰减小，旁瓣清晰，随着衰减系数的增大，艾里光束的衰减也在增大，当其为1时，可见旁瓣已经全部衰减，只留下主瓣光束，艾里光束变为类高斯光束。

3 结语

本文对高斯光束和艾里光束进行了理论分析和实验模拟。在高斯光束部分的实验中，验证了符合单一波长高斯光束经过傅里叶变换后的归一化后的幅频特性以及高斯波束傅里叶变换时不受波长影响的特性，发现随着焦距的增大，最后得到的图像上频点的直径也随之增大，且其他条件不变，增大束腰半径，可得到更多的频谱细节。在艾里光束部分的实验中，验证了艾里光束的自加速特性，发现艾里光束的频谱图与高斯光束的有相似之处，如有相似的十字亮线以及中间亮斑，不同的是由于艾里光束除了主瓣以外，有多个旁瓣，这些旁瓣的存在在频谱图上的表现是产生了中心亮点以外的小亮点；随着艾里光束的衰减系数增大，其频谱图频点在减少，当衰减系数增大至1时，其频谱图只有一个频点。