谈谈一个特殊的集合——空集

张洢茼

(河北省石家庄市精英中学 050035)

空集是一个极其特殊又非常重要的集合，它不含任何元素，正因为空集的特殊性，常常成为各类考试的热点.而在解题过程中常因忽视空集的特殊性而导致错解，所以我们在学习过程中一定要谨慎小心.

对于空集∅，在解题时必须注意它的三个性质：

①对任意集合A，都有∅∩A=∅和∅∪A=A；

②对任意集合A，都有∅⊆A；

③对任意非空集合A，都有∅A．

解题时若忽视∅的存在性，就会造成解题结果的残缺不全．下面举几例说明，以供同学们参考．

例1 设集合A= {x|x2+4x=0，x∈R}，B={x|x2+2(a+1)x+a2-1= 0，a∈R，x∈R}，若B⊆A，求实数a的取值范围．

错解∵A= {0，-4}，

∴B⊆A分以下两种情况：

(1)当B=A时，B= {0，-4}，由此知：0和-4是方程x2+2(a+1)x+a2-1= 0的两个根，由根与系数之间的关系，得：

⟹a= 1．

(2)当BA时，B={0}或B= {-4}，并且Δ=4(a+1)2-4(a2-1)=0，解得a=-1，此时B={0}满足题意．

综合(1)、(2)知，所求实数a的值为a=-1或a=1．

剖析错解只注意到B为非空集合，丢掉了B=∅时的情况，当B为空集∅时仍满足B⊆A．因此，B⊆A可分为B=∅，BA，B=A三种情况讨论．

正解除了前面两种情况外，还有B=∅时，此时Δ=4(a+1)2-4(a2-1)<0，解得a<-1．

综合前面三种情况知，所求实数a的值为a≤-1或a=1．

例2 若集合A={x|x2+x-6=0}，B={x|mx+1=0}，且A∩B=B，求m的值.

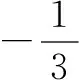
剖析错解只考虑B≠∅时的情况，当B=∅时，同样有A∩B=B成立.

正解易得A={x|x2+x-6=0}={-3，2}.

∵A∩B=B，

∴当B=∅时，m=0适合题意；

例3 已知集合A={x|x2-5x+6=0}，集合B={x|ax-4=0}，且A∪B=A，求实数a的值组成的集合C．

错解由x2-5x+6=0，得x=2或x=3.

当x=2时，a=2；

剖析上述解答只注意了B为非空集合，实际上，B=∅时，仍满足A∪B=A，当a=0时，B=∅，符合题意．上述解答忽略了“空集是任何集合的子集”这一结论．

正解∵A∪B=A，∴B⊆A．

当B=∅时，a=0．

∵当B≠∅时，由x2-5x+6=0，得x=2或x=3．

当x=2时，a=4；

例4 已知A={||x-1|≤a}，B={x|x<-6或x>4}，且A∩B=∅，求实数a的取值范围.

分析由于集合B不是空集，对集合A的化简和辨别是首先要解决的问题.

解(1)当a<0时，由于|x-1|是非负数，故A=∅，这时A∩B=∅，符合题意；

(2)当a=0时，A={||x-1|≤0}={1}，此时A∩B=∅，也符合题意；

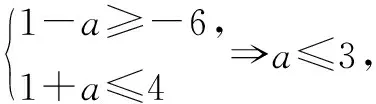
综合得，实数a的取值范围是a≤3.

例5 已知集合A={x|x2-3x+2=0},B={x|x2-ax+3a-5=0},若A∩B=B,求实数a的值.

解A={x|x2-3x+2=0}={1,2},

由x2-ax+3a-5=0知Δ=a2-4(3a-5)=a2-12a+20=(a-2)(a-10).

(1)当2

(2)当a≤2或a≥10时，Δ≥0.

若x=1，由1-a+3a-5=0即a=2，此时B={x|x2-2x+1=0}={1}⊆A;

若x=2，由4-2a+3a-5=0，即a=1，此时B={2,-1}A.

由(1)(2)可知，当2≤a<10时，均有A∩B=B.

说明通过以上例题，我们发现尤其在求解有关集合的交集、并集的时候，特别要注意不要丢掉空集这一特殊情况.同学们在学习新知识的时候要善于总结，以防出错．